Description
We remind that the permutation of some final set is a one-to-one mapping of the set onto itself. Less formally, that is a way to reorder elements of the set. For example, one can define a permutation of the set {1,2,3,4,5} as follows:

This record defines a permutation P as follows: P(1) = 4, P(2) = 1, P(3) = 5, etc.
What is the value of the expression P(P(1))? It’s clear, that P(P(1)) = P(4) = 2. And P(P(3)) = P(5) = 3. One can easily see that if P(n) is a permutation then P(P(n)) is a permutation as well. In our example (believe us)
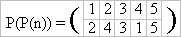
It is natural to denote this permutation by P2(n) = P(P(n)). In a general form the defenition is as follows: P(n) = P1(n), Pk(n) = P(Pk-1(n)). Among the permutations there is a very important one — that moves nothing:

It is clear that for every k the following relation is satisfied: (EN)k = EN. The following less trivial statement is correct (we won't prove it here, you may prove it yourself incidentally): Let P(n) be some permutation of an N elements set. Then there exists a natural number k, that Pk = EN. The least natural k such that Pk = EN is called an order of the permutation P.
The problem that your program should solve is formulated now in a very simple manner: "Given a permutation find its order."

This record defines a permutation P as follows: P(1) = 4, P(2) = 1, P(3) = 5, etc.
What is the value of the expression P(P(1))? It’s clear, that P(P(1)) = P(4) = 2. And P(P(3)) = P(5) = 3. One can easily see that if P(n) is a permutation then P(P(n)) is a permutation as well. In our example (believe us)
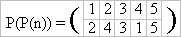
It is natural to denote this permutation by P2(n) = P(P(n)). In a general form the defenition is as follows: P(n) = P1(n), Pk(n) = P(Pk-1(n)). Among the permutations there is a very important one — that moves nothing:

It is clear that for every k the following relation is satisfied: (EN)k = EN. The following less trivial statement is correct (we won't prove it here, you may prove it yourself incidentally): Let P(n) be some permutation of an N elements set. Then there exists a natural number k, that Pk = EN. The least natural k such that Pk = EN is called an order of the permutation P.
The problem that your program should solve is formulated now in a very simple manner: "Given a permutation find its order."
Input
In
the first line of the standard input an only natural number N (1 <= N
<= 1000) is contained, that is a number of elements in the set that
is rearranged by this permutation. In the second line there are N
natural numbers of the range from 1 up to N, separated by a space, that
define a permutation — the numbers P(1), P(2),…, P(N).
Output
You
should write an only natural number to the standard output, that is an
order of the permutation. You may consider that an answer shouldn't
exceed 109.
Sample Input
5
4 1 5 2 3
Sample Output
6
求出循环,每个循环都是独立的,所以所需次数就是所有循环长度的最小公倍数
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<cmath> 6 using namespace std; 7 int vis[1001],s[1001],tot,a[1001],n,ans; 8 int dfs(int x,int cnt) 9 { 10 if (vis[x]) return cnt; 11 vis[x]=1; 12 return dfs(a[x],cnt+1); 13 } 14 int gcd(int x,int y) 15 { 16 if (y==0) return x; 17 return gcd(y,x%y); 18 } 19 int lcm(int x,int y) 20 { 21 return x*y/gcd(x,y); 22 } 23 int main() 24 {int i; 25 cin>>n; 26 for (i=1;i<=n;i++) 27 scanf("%d",&a[i]); 28 for (i=1;i<=n;i++) 29 if (vis[i]==0) 30 { 31 s[++tot]=dfs(i,0); 32 } 33 ans=s[1]; 34 for (i=2;i<=tot;i++) 35 { 36 ans=lcm(ans,s[i]); 37 } 38 cout<<ans; 39 }