CF519E

 

因为蒟蒻我很弱（而且第一次发题解）所以很可能会出错，欢迎各位大佬指出。

简单分析一下题意：有m次询问，每次回答求到A与B两点距离相等的点的个数。

以下图为例，把一号节点当作根节点。

 　　　　　　　　

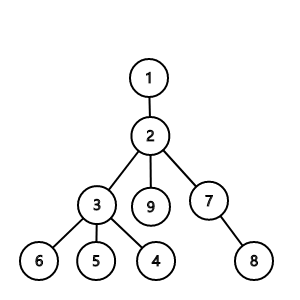
特殊情况：所求点A与点B重合，那任意点到A与B的距离都相等；

一：两点之间点数为偶数，无解；

二：两点之间点数为奇数时

情况一：当A与B深度不同且有一节点深度等于小于中点时，答案为 中点儿子数 - 包含较深节点子树节点数 + 1（因为在计数时已经把根节点算入，所以代码中没有+1）.

　　　　　　　　

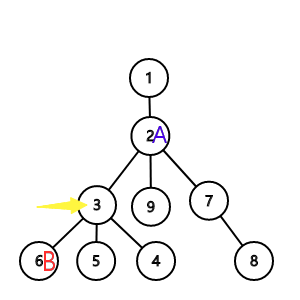
情况二：A与B深度都大于中点深度，且A与B都在中点子树中。从图像可以为我们看出答案为中点子节点数 - 包含A与B的两颗子树的节点数 + 1.

　　

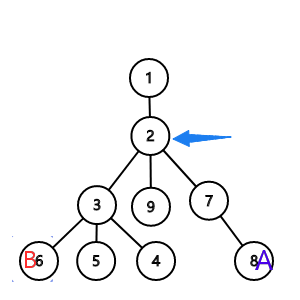
情况三：A与B深度都大于中点深度，但有一点不与中点在同一子树中。我们可以看出这与情况一相似因为路径必须经过中点的父亲节点所以答案为 中点儿子数 - 包含较深节点子树节点数 + 1。

 

 

 

 

 

 

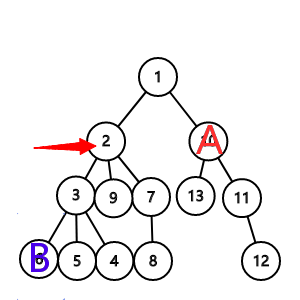
#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;

const int N = 1e5 + 10;

int n, tot, s, m, A, B, k, h;
int dth[N], head[N], fa[N][24], lg[N], sum[N];

struct Edge {
	int to, nxt;
}e[N << 1];

template <typename T>
inline void read(T& x) {
	x = 0;
	char c = getchar();
	T op = 1;
	for (; c < '0' || c > '9'; c = getchar())
		if (c == '-')	op = -1;
	for (; c <= '9' && c >= '0'; c = getchar())
		x = (x << 3) + (x << 1) + c - '0';
	x *= op;
}

inline void add(int x, int y) {
	e[++tot].to = y;
	e[tot].nxt = head[x];
	head[x] = tot;
}

void dfs(int x, int fath) {
	dth[x] = dth[fath] + 1;
	fa[x][0] = fath;
	sum[x] = 1;
	for (int i = 1; i <= s; ++i)
		fa[x][i] = fa[fa[x][i - 1]][i - 1];
	for (int i = head[x]; i; i = e[i].nxt)
		if (e[i].to != fath)	dfs(e[i].to, x), sum[x] += sum[e[i].to];
}

inline void init() {
	for (int i = 1; i <= n; ++i)
		lg[i] = lg[i - 1] + (1 << lg[i - 1] == i);
}

inline int lca(int x, int y) {
	if (dth[x] < dth[y])	swap(x, y);
	while (dth[x] > dth[y])	x = fa[x][lg[dth[x] - dth[y]] - 1];
	if (x == y)	return x;
	for (int i = lg[dth[x]] - 1; i >= 0; --i)
		if (fa[x][i] != fa[y][i])	x = fa[x][i], y = fa[y][i];
	return fa[x][0];
}

inline int ask() {
	int z = dth[A] + dth[B] - (dth[k] << 1) - 1;
	if (dth[A] < dth[B])	swap(A, B);
	int x = A, f = A;
	for (int i = s; i >= 0; --i)
		if (dth[A] - dth[fa[x][i]] <= (z + 1) >> 1 && fa[x][i])	x = fa[x][i];//求两点路径上的中点
	for (int i = s; i >= 0; --i)
		if (dth[x] < dth[fa[f][i]] && fa[f][i]) f = fa[f][i];//找到包含较深点的子树
	if (dth[k] >= dth[B])	return	sum[x] - sum[f];//情况一
	else {
		int q = B;
		for (int i = s; i >= 0; --i)
			if (dth[x] < dth[fa[q][i]] && fa[q][i]) q = fa[q][i];
		if (fa[q][0] == k) //判断是否在同一子树内	
            return n - sum[f] - sum[q];//情况二
		else return	sum[x] - sum[f];//情况三
	}
}

int main() {
	read(n);
	init();
	s = log2(n) + 1;
	for (int i = 1; i < n; ++i) {
		int x, y;
		read(x), read(y);
		add(x, y), add(y, x);
	}
	dfs(1, 0);
	read(m);
	for (h = 1; h <= m; ++h) {
		read(A), read(B);
		if (A == B) { printf("%d
", n); continue; }//特殊情况
		k = lca(A, B);//求LCA
		if ((dth[A] - (dth[k] << 1) + dth[B]) & 1)	printf("0
");//两点之间点数为偶数时无解
		else printf("%d
", ask());
	}
	return 0;
}