122. Best Time to Buy and Sell Stock II ——LeetCode

Say you have an array for which the ith element is the price of a given stock on day i.

Design an algorithm to find the maximum profit. You may complete as many transactions as you like (i.e., buy one and sell one share of the stock multiple times).

Note: You may not engage in multiple transactions at the same time (i.e., you must sell the stock before you buy again).

Example 1:

Input: [7,1,5,3,6,4]
Output: 7
Explanation: Buy on day 2 (price = 1) and sell on day 3 (price = 5), profit = 5-1 = 4.
             Then buy on day 4 (price = 3) and sell on day 5 (price = 6), profit = 6-3 = 3.

Example 2:

Input: [1,2,3,4,5]
Output: 4
Explanation: Buy on day 1 (price = 1) and sell on day 5 (price = 5), profit = 5-1 = 4.
             Note that you cannot buy on day 1, buy on day 2 and sell them later, as you are
             engaging multiple transactions at the same time. You must sell before buying again.

Example 3:

Input: [7,6,4,3,1]
Output: 0
Explanation: In this case, no transaction is done, i.e. max profit = 0.

题目大意：与上一题类似，只不过没有次数限制。求最大获利。

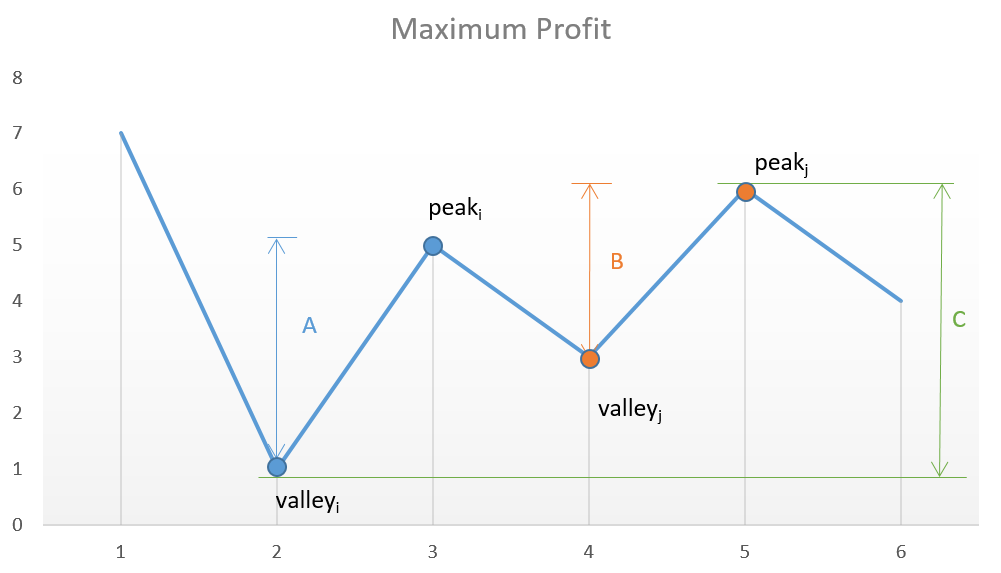
思路：如果一直递增，那么最后一个元素减去第一个元素就是当前区间最大获利，没疑问吧。如果类似于1 3 2 4这种山峰似的，将每个递增子区间的获利加起来，就是最大获利。

Solution中有个图片看一眼就知道了。

 public int maxProfit(int[] arr) {
     if (arr == null ||arr.length == 0) {
         return 0;
     }
     int len = arr.length;
     int i = 1;
     int start = 0;
     int res = 0;
     while(i<len) {
         while(i<len && arr[i] > arr[i-1]) {
             i++;
         }
         res += Math.max(arr[i-1] - arr[start], 0);
         start = i;
         i++;
     }
     return res;
 }