本文来自:挑战程序竞赛
以下是我的总结
题目:有n块石头排成一圈。现在要用m种颜色染这n块石头,问一共有多少种不同的染色方案。旋转之后相同的方案视作同一种。输出方案数 mod 1e9+7。
n的范围最大是1e9!!!
题解:
polya计数!!!
我们分n个转角,那么对于转的角度是k个石头的方案数来说:若旋转k个位置之后和原来的相同,那么第i个石头与第(i+k)%n 的石头颜色应该是一样的!!!那么按这个递推下去
第i个石头与第(i+tk)%n 的石头的颜色也应该是一样的。 这样我们就能用 gcd(n,k)判断有多少个循环节 ,然后用n/gcd(n,k)就可以算出循环节的长度。
然后i的轨迹为 i->(i+k) mod n -> (i+2k) mod n -> …… -> (i+k*t) mod n == i
那么对于转角为k,我们将n个石头都划分成这样的若干条轨迹 ,每条轨迹的颜色都染成同样的,那么只要知道轨迹条数就能知道转角为k的染色方案!。这就等于判断有多少个这样的循环节
也就是gcd(n,k) 那么染色方案为 m^(gcd(k,n))
由于n范围为1e9,枚举转角不科学!!!所以我们要统计gcd(k,n)=d的k的个数。很显然 k是d的倍数那么能推出 gcd(dt,n)=d -> gcd(t,n/d) = 1推到这里很容易发现,这个东西就是
求欧拉函数,即求比n/d小的数里面有多少个与 n/d 互质。
那么公式就有了 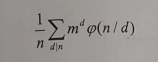
由于这个要求d|n的所有欧拉值,所以不能硬算,又不能先预处理,因为n太大。所以考虑欧拉函数的基本定理
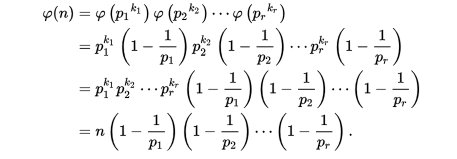
所以我们只要预处理出n的所有质因数,然后就可以很快的算出每个因子的欧拉值
时间复杂度大概是(sqrt(n))
详见代码:

/*********************************************** * _ooOoo_ * * o8888888o * * 88" . "88 * * (| -_- |) * * O = /O * * ____/`---'\____ * * .' \| |// `. * * / \||| : |||// * * / _||||| -:- |||||- * * | | \ - * | | * * | \_| ''---/'' | | * * .-\__ `-` ___/-. / * * ___`. .' /--.-- `. . __ * * ."" '< `.___\_<|>_/___.' >'"". * * | | : `- \`.;` _ /`;.`/ - ` : | | * * `-. \_ __ /__ _/ .-` / / * *======`-.____`-.___\_____/___.-`____.-'======* * `=---=' * *^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ 佛祖保佑 永无BUG 本程序已经经过开光处理,绝无可能再产生bug **********************************************/ /*** . ';;;;;. '!;;;;;;!;` '!;|&#@|;;;;!: `;;!&####@|;;;;!: .;;;!&@$$%|!;;;;;;!'.`:::::'. '!;;;;;;;;!$@###&|;;|%!;!$|;;;;|&&;. :!;;;;!$@&%|;;;;;;;;;|!::!!:::;!$%;!$%` '!%&#########@$!:. ;!;;!!;;;;;|$$&@##$;;;::'''''::;;;;|&|%@$|;;;;;;;;;;;;;;;;!$; ;|;;;;;;;;;;;;;;;;;;!%@#####&!:::;!;;;;;;;;;;!&####@%!;;;;$%` `!!;;;;;;;;;;!|%%|!!;::;;|@##%|$|;;;;;;;;;;;;!|%$#####%;;;%&; :@###&!:;;!!||%%%%%|!;;;;;||;;;;||!$&&@@%;;;;;;;|$$##$;;;%@| ;|::;;;;;;;;;;;;|&&$|;;!$@&$!;;;;!;;;;;;;;;;;;;;;;!%|;;;%@%. `!!;;;;;;;!!!!;;;;;$@@@&&&&&@$!;!%|;;;;!||!;;;;;!|%%%!;;%@|. %&&$!;;;;;!;;;;;;;;;;;|$&&&&&&&&&@@%!%%;!||!;;;;;;;;;;;;;$##! !%;;;;;;!%!:;;;;;;;;;;!$&&&&&&&&&&@##&%|||;;;!!||!;;;;;;;$&: ':|@###%;:;;;;;;;;;;;;!%$&&&&&&@@$!;;;;;;;!!!;;;;;%&!;;|&%. !@|;;;;;;;;;;;;;;;;;;|%|$&&$%&&|;;;;;;;;;;;;!;;;;;!&@@&' .:%#&!;;;;;;;;;;;;;;!%|$$%%&@%;;;;;;;;;;;;;;;;;;;!&@: .%$;;;;;;;;;;;;;;;;;;|$$$$@&|;;;;;;;;;;;;;;;;;;;;%@%. !&!;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;|@#; `%$!;;;;;;;;;;;$@|;;;;;;;;;;;;;;;;;;;;;;;;!%$@#@|. .|@%!;;;;;;;;;!$&%||;;;;;;;;;;;;;;;;;!%$$$$$@#|. ;&$!;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;%#####|. |##$|!;;;;;;::'':;;;;;;;;;;;;;!%$$$@#@; ;@&|;;;;;;;::'''''':;;;;;;;|$&@###@|` .%##@|;;;;:::''''''''''::;!%&##$' `$##@$$@@&|!!;;;:'''''::::;;;;;|&#%. ;&@##&$%!;;;;;;::''''''''::;!|%$@#@&@@: .%@&$$|;;;;;;;;;;:'''':''''::;;;%@#@@#%. :@##@###@$$$$$|;;:'''':;;!!;;;;;;!$#@@#$;` `%@$$|;;;;;;;;:'''''''::;;;;|%$$|!!&###&' |##&%!;;;;;::''''''''''''::;;;;;;;!$@&:`!' :;!@$|;;;;;;;::''''''''''':;;;;;;;;!%&@$: !@#$' |##@@&%;;;;;::''''''''':;;;;;;;!%&@#@$%: '%%!%&; |&%!;;;;;;;%$!:''''''':|%!;;;;;;;;|&@%||` '%$|!%&; |@%!;;!!;;;||;:'''''':;%$!;;;;!%%%&#&%$&: .|%;:!&%` !@&%;;;;;;;||;;;:''::;;%$!;;;;;;;|&@%;!$; `%&%!!$&: '$$|;!!!!;;||;;;;;;;;;;%%;;;;;;;|@@|!$##; !$!;:!$&: |#&|;;;;;;!||;;;;;;;;!%|;;;;!$##$;;;;|%' `%$|%%;|&$' |&%!;;;;;;|%;;;;;;;;$$;;;;;;|&&|!|%&&; .:%&$!;;;:!$@! `%#&%!!;;;;||;;;;;!$&|;;;!%%%@&!;;;!!;;;|%!;;%@$!%@! !&!;;;;;;;;;||;;%&!;;;;;;;;;%@&!;;!&$;;;|&%;;;%@%` '%|;;;;;;;;!!|$|%&%;;;;;;;;;;|&#&|!!||!!|%$@@|' .!%%&%'`|$; :|$#%|@#&;%#%. * ii. ;9ABH, * SA391, .r9GG35&G * &#ii13Gh; i3X31i;:,rB1 * iMs,:,i5895, .5G91:,:;:s1:8A * 33::::,,;5G5, ,58Si,,:::,sHX;iH1 * Sr.,:;rs13BBX35hh11511h5Shhh5S3GAXS:.,,::,,1AG3i,GG * .G51S511sr;;iiiishS8G89Shsrrsh59S;.,,,,,..5A85Si,h8 * :SB9s:,............................,,,.,,,SASh53h,1G. * .r18S;..,,,,,,,,,,,,,,,,,,,,,,,,,,,,,....,,.1H315199,rX, * ;S89s,..,,,,,,,,,,,,,,,,,,,,,,,....,,.......,,,;r1ShS8,;Xi * i55s:.........,,,,,,,,,,,,,,,,.,,,......,.....,,....r9&5.:X1 * 59;.....,. .,,,,,,,,,,,... .............,..:1;.:&s * s8,..;53S5S3s. .,,,,,,,.,.. i15S5h1:.........,,,..,,:99 * 93.:39s:rSGB@A; ..,,,,..... .SG3hhh9G&BGi..,,,,,,,,,,,,.,83 * G5.G8 9#@@@@@X. .,,,,,,..... iA9,.S&B###@@Mr...,,,,,,,,..,.;Xh * Gs.X8 S@@@@@@@B:..,,,,,,,,,,. rA1 ,A@@@@@@@@@H:........,,,,,,.iX: * ;9. ,8A#@@@@@@#5,.,,,,,,,,,... 9A. 8@@@@@@@@@@M; ....,,,,,,,,S8 * X3 iS8XAHH8s.,,,,,,,,,,...,..58hH@@@@@@@@@Hs ...,,,,,,,:Gs * r8, ,,,...,,,,,,,,,,..... ,h8XABMMHX3r. .,,,,,,,.rX: * :9, . .:,..,:;;;::,.,,,,,.. .,,. ..,,,,,,.59 * .Si ,:.i8HBMMMMMB&5,.... . .,,,,,.sMr * SS :: h@@@@@@@@@@#; . ... . ..,,,,iM5 * 91 . ;:.,1&@@@@@@MXs. . .,,:,:&S * hS .... .:;,,,i3MMS1;..,..... . . ... ..,:,.99 * ,8; ..... .,:,..,8Ms:;,,,... .,::.83 * s&: .... .sS553B@@HX3s;,. .,;13h. .:::&1 * SXr . ...;s3G99XA&X88Shss11155hi. ,;:h&, * iH8: . .. ,;iiii;,::,,,,,. .;irHA * ,8X5; . ....... ,;iihS8Gi * 1831, .,;irrrrrs&@ * ;5A8r. .:;iiiiirrss1H * :X@H3s....... .,:;iii;iiiiirsrh * r#h:;,...,,.. .,,:;;;;;:::,... .:;;;;;;iiiirrss1 * ,M8 ..,....,.....,,::::::,,... . .,;;;iiiiiirss11h * 8B;.,,,,,,,.,..... . .. .:;;;;iirrsss111h * i@5,:::,,,,,,,,.... . . .:::;;;;;irrrss111111 * 9Bi,:,,,,...... ..r91;;;;;iirrsss1ss1111***/ #include <bits/stdc++.h> using namespace std; #define ll long long #define re register const int N=1e5+10; const int M=1e5; const int mod=1e9+7; void read(int &a) { a=0;int d=1;char ch; while(ch=getchar(),ch<'0'||ch>'9') if(ch=='-') d=-1; a=ch^48; while(ch=getchar(),ch>='0'&&ch<='9') a=(a<<3)+(a<<1)+(ch^48); a*=d; } int b[N],cnt,a[N],tot; void init(int n)///筛因子 { int p=sqrt(n); for(re int i=1;i<=p;i++) { if(n%i==0) { if(i!=n/i) b[cnt++]=i,b[cnt++]=n/i; else b[cnt++]=i; } } } void div(int x)///筛质因数 { for(re int i=2;i*i<=x;i++) { if(x%i==0) { a[tot++]=i; while(x%i==0) x/=i; } } if(x>1) a[tot++]=x; } ll quickmod(ll x,ll y) { ll res=1; ll base=x; while(y) { if(y&1) res=res*base%mod; base=base*base%mod; y>>=1; } return res; } ///a数组存的是质因子,b数组存的是因子。 int main() { int n,m; read(n),read(m); init(n); div(n); ll ans=0; //cout<<cnt<<endl; for(re int i=0;i<cnt;i++) { ll euler=n/b[i],x=n/b[i]; for(re int j=0;j<tot;j++) if(x%a[j]==0) euler=euler/a[j]*(a[j]-1); //cout<<n/b[i]<<" "<<euler<<endl; ans+=euler*quickmod(m,b[i])%mod; ans%=mod; } ans=ans*quickmod(n,mod-2)%mod; printf("%lld",ans); return 0; }
