堆排序

版权所有： 博客园Anders06    于 2007年11月14日

堆：是一颗完全二叉树，数的每一层都是填满的，最后一层可能除外。
最大堆：满足所有结点的子结点比其自身小的堆
最小堆：满足所有结点的子结点比其自身大的堆

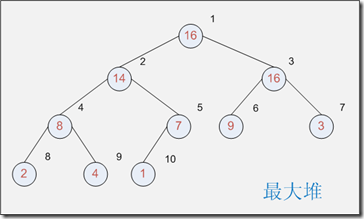
设某结点下标为i，则

其父结点下标为 Parent（i） = |_  i / 2 _|
其左儿子下标为 Left（i） = 2i
其右儿子下标为 Right（i）= 2i + 1

堆的高度为 lgN

保持堆(最大堆)算法:

找出下标为i, Left(i), Right(i)三者中值最大的结点下标. 如果最大值下标为i则结束此过程; 如果最大值下标为i的子结点,则将其与下标为i的结点交换. 递归对交换后的子数做同样的动作.

（约束： i结点的2个子树都是最大堆）

保持堆算法
 /// <summary>
 /// Keep the array as max heap
 /// The node of adjustIndex may has destroy the array as max heap, 
 /// adjust it to restore sortArray[0arrayLength] as max heap
 /// </summary>
 /// <param name="sortArray">The array</param>
 /// <param name="adjustIndex">Need to be adjust index</param>
 /// <param name="arrayLength">The length of sortArray need to be adjusted</arrayLength>
 private static void MaxHeapify(T[] sortArray, int adjustIndex, int arrayLength)
 {
     Debug.Assert(adjustIndex >= 0 && adjustIndex < arrayLength);

     int leftIndex = Left(adjustIndex);        // get left child index
     int rightIndex = Right(adjustIndex);      // get right child index

     if (leftIndex >= arrayLength)  // has no children
         return;

     int largest = adjustIndex;
     if (sortArray[leftIndex].CompareTo(sortArray[largest]) >= 0)
         largest = leftIndex;
     
     // make sure have right child
     if (rightIndex < arrayLength && sortArray[rightIndex].CompareTo(sortArray[largest]) > 0)
         largest = rightIndex;

     if (adjustIndex != largest)
     {
         Exchange(sortArray, adjustIndex, largest);  // change the two nodes
         MaxHeapify(sortArray, largest, arrayLength);             // Recursion keep the sub tree
     }
 }

 /// <summary>
 /// Exchange the two nodes
 /// </summary>
 /// <param name="sortArray"></param>
 /// <param name="oneIndex"></param>
 /// <param name="anotherIndex"></param>
 private static void Exchange(T[] sortArray, int oneIndex, int anotherIndex)
 {
     T temp = sortArray[oneIndex];
     sortArray[oneIndex] = sortArray[anotherIndex];
     sortArray[anotherIndex] = temp;
 }

 /// <summary>
 /// Get the left child index
 /// </summary>
 /// <param name="index"></param>
 /// <returns></returns>
 private static int Left(int index)
 {
     return (index * 2) + 1;
 }

 /// <summary>
 /// Get the right child index
 /// </summary>
 /// <param name="index"></param>
 /// <returns></returns>
 private static int Right(int index)
 {
     return Left(index) + 1;
 }

建堆：

我们可以利用保持堆算法自底向上地建堆。因为所有叶子结点没有子树所以没有必要调用最大堆算法调整。
我们知道一个结点如果没有左儿子其就为叶子结点， 因Left（i） = 2i， 所以 当2i > N时 就表明结点i是叶子结点

建最大堆
 /// <summary>
 /// Build a max heap
 /// </summary>
 /// <param name="sortArray">The array</param>
 private static void BuildMaxHeap(T[] sortArray)
 {
     // The sortArray[sortArray.Length / 2)  sortArray.Length -1] element is a leaf,
     // need not call keep max heap function
     for (int i = (sortArray.Length / 2) - 1; i >= 0; i--)  
         MaxHeapify(sortArray, i, sortArray.Length);
 }

堆排序算法

（1）用最大堆排序的基本思想
① 先将初始文件R[1..n]建成一个最大堆，此堆为初始的无序区
② 再将关键字最大的记录R[1](即堆顶)和无序区的最后一个记录R[n]交换，由此得到新的无序区R[1..n-1]和有序区R[n]，且满足R[1..n-1].keys≤R[n].key
③ 由于交换后新的根R[1]可能违反堆性质，故应将当前无序区R[1..n-1]调整为堆。然后再次将R[1..n-1]中关键字最大的记录R[1]和该区间的最后一个记录R[n-1]交换，由此得到新的无序区R[1..n-2]和有序区R[n-1..n]，且仍满足关系R[1..n-2].keys≤R[n-1..n].keys，同样要将R[1..n-2]调整为堆。
    ……
直到无序区只有一个元素为止。

堆排序
/// <summary>
/// Sort the array
/// </summary>
/// <param name="sortArray">The array need to be sort</param>
public static void Sort(T[] sortArray)
{
    BuildMaxHeap(sortArray); // build the max heap
    for (int i = (sortArray.Length - 1); i > 0; i--)
    {
        Exchange(sortArray, 0, i);
        MaxHeapify(sortArray, 0, i);
    }
}

算法分析

堆排序的最坏时间复杂度为O(nlgn)。堆排序的平均性能较接近于最坏性能。
由于建初始堆所需的比较次数较多，所以堆排序不适宜于记录数较少的文件。
堆排序是就地排序，辅助空间为O(1)，
它是不稳定的排序方法。

参考

数据结构自考网 -- 堆排序

<<算法导论>>