优先队列 安静点

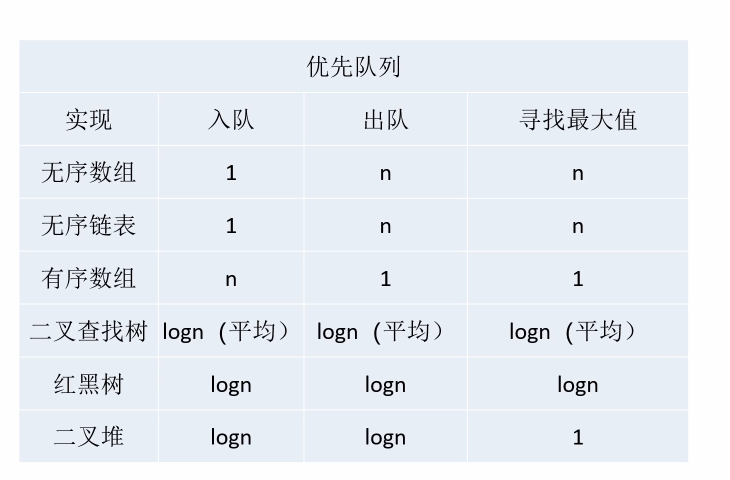
优先队列  

比如现实生活中的排队，就符合这种先进先出的队列形式，但是像急诊医院排队，就不可能按照先到先治疗的规则，所以需要使用优先队列。

实现优先队列其实都是基于下面这些实现的：可以看出来实现优先队列最好的方式就是二叉堆。

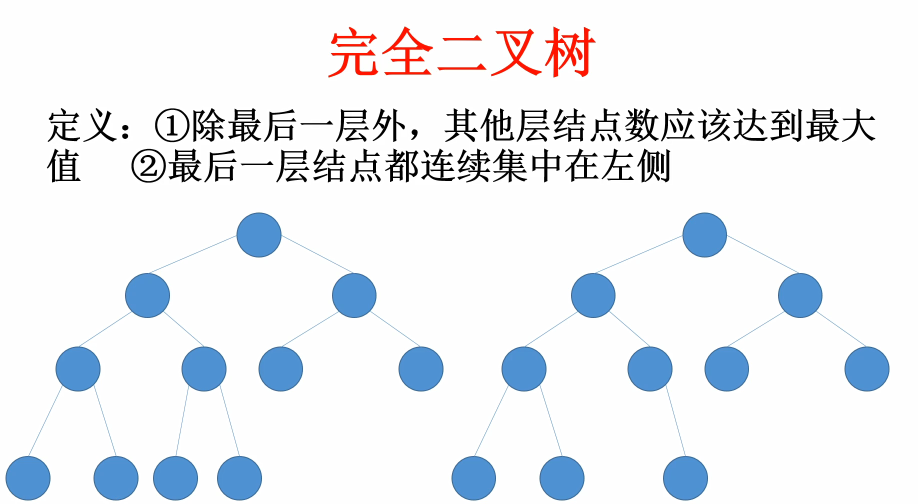
 （1）二叉堆本质上是一种完全二叉树 

比如下面2棵树，左边的树是完全二叉树，右边不是，因为没有连续集中在左侧。定义1的意思是指

二叉堆的定义：

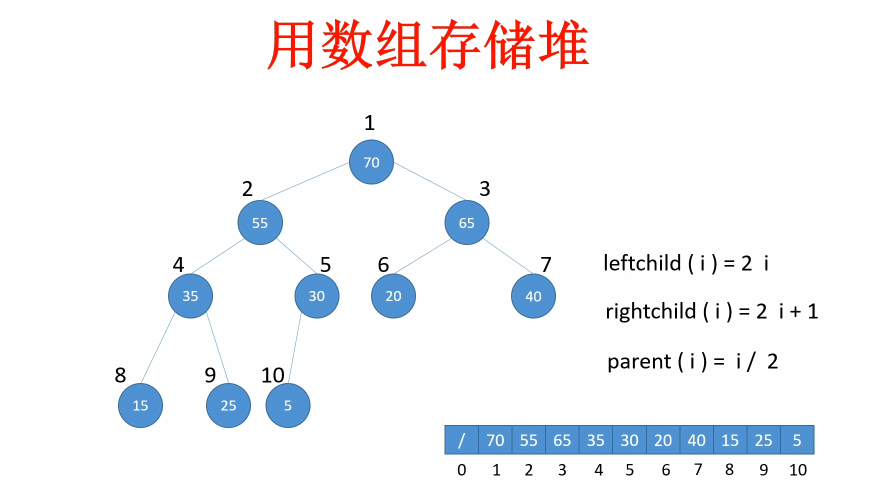
用数组来存储堆：如下图，父节点左孩子节点是本身索引的2倍，右孩子节点的索引是本身节点的2倍+1，这样只要知道其中一个节点的信息，就能迅速知道父节点或对应孩子节点的信息了。

最大堆

二叉堆分为2个类型，最大堆和最小堆，对于最大堆：最大堆任何一个父节点的值，都大于等于它左右孩子节点的值。

所以在插入新值68的时候，首先要满足作为完全二叉树的条件，就是最下层节点必须连续集中在左侧，所以放在11的位置，如下图：

如果这个二叉堆是最大堆，那么需要元素上游，和对应父节点进行比较，结果如下图：

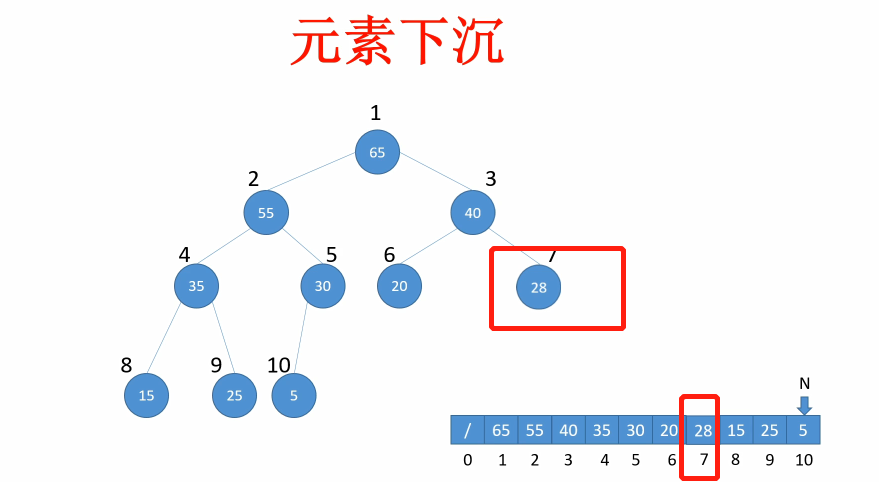
如果我们要删除其中一个元素，比如根节点70，那我们需要将70和最下层的最右边的一个节点进行交换，然后删除70，如下：

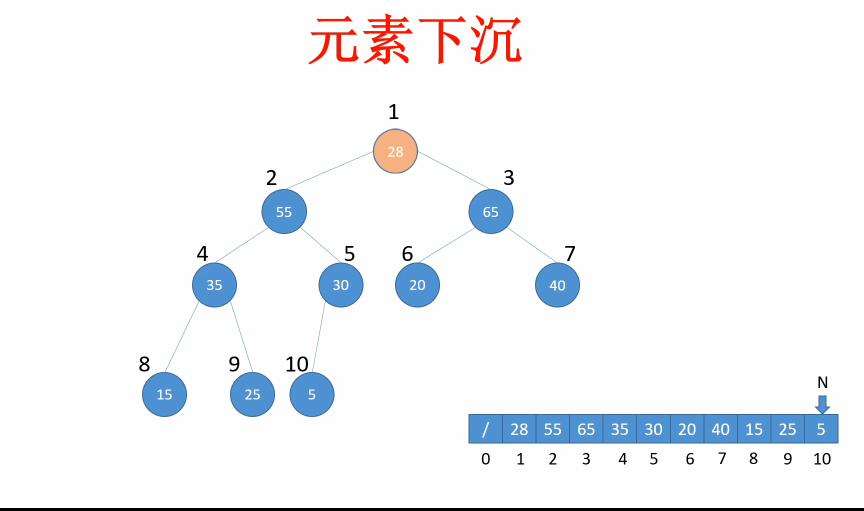
但是此时明显不符合最大堆的定义，所以进行元素下沉：55和65都比28要大，但是我们选择和65交换，因为要满足最大堆的定义，这是风险最小的选择。

 代码实现:

namespace DataStructure
{
    /// <summary>
    /// 数组堆
    /// </summary>
    /// <typeparam name="E"></typeparam>
    class MaxHeap<E> where E : IComparable<E>
    {

        private E[] heap;
        private int N;
        public MaxHeap(int capacity)
        {
            //之所以加1，是因为索引为0的地方是没有存值的。
            heap = new E[capacity + 1];
        }

        public MaxHeap() : this(10)
        {

        }

        public int Count { get { return N; } }
        public bool IsEmpty { get { return N == 0; } }

        public void Insert(E e)
        {
            //之所以减一，是因为二叉堆中的具体数是在索引1处开始。
            if (N == heap.Length - 1)
            {
                ResetCapacity(heap.Length * 2);
            }

            //首先保证此树是完全二叉树。
            heap[N + 1] = e;
            N++;
            Swim(N);
        }
        /// <summary>
        /// 元素上游
        /// </summary>
        /// <param name="k"></param>
        private void Swim(int k)
        {
            //k==1时代表找到了根节点，所以不用再比较了，不能上游了
            while (k > 1 && heap[k].CompareTo(heap[k / 2]) > 0)
            {
                Swap(k, k / 2);
                k = k / 2;
            }

        }

        private void Swap(int i, int j)
        {
            E e = heap[i];
            heap[i] = heap[j];
            heap[j] = e;
        }
        //删除最大元素
        public E RemoveMax()
        {
            if (IsEmpty)
                throw new Exception("堆为空");
            Swap(1, N);
            E max = heap[N];
            //设置默认值，让垃圾回收器GC进行回收。
            heap[N] = default;
            N--;
            Sink(1);
            if (N == (heap.Length - 1) / 4)
                ResetCapacity(heap.Length / 2);
            return max;
        }
        /// <summary>
        ///返回最大值
        /// </summary>
        /// <returns></returns>
        public E Max()
        {
            if (IsEmpty)
                throw new Exception("堆为空");
            return heap[1];
        }

        /// <summary>
        /// 元素下沉
        /// </summary>
        /// <param name="k"></param>
        private void Sink(int k)
        {
            //当前存在孩子节点的时候才能往下比较
            while (2 * k <= N)
            {
                int j = 2 * k;
                //j+1<=N表示存在右孩子节点，
                //如果存在右孩子节点，并且右孩子节点比左孩子节点大
                if (j + 1 <= N && heap[j + 1].CompareTo(heap[j]) > 0)
                {
                    //右孩子的位置
                    j++;
                }
                //如果当前节点大于右孩子节点，则跳出
                if (heap[k].CompareTo(heap[j]) >= 0)
                {
                    break;
                }

                Swap(k, j);
                //j代表交换完成之后元素所在的新的位置，赋给k，看看这个位置是否需要继续交换
                k = j;
            }

        }

        /// <summary>
        /// 数组扩容
        /// </summary>
        /// <param name="newLength"></param>
        private void ResetCapacity(int newLength)
        {
            E[] newData = new E[newLength];
            //将旧有数据复制到扩容后的新数组中
            heap.CopyTo(newData, 0);
            //赋值给原有数组 注意此时给data的是引用，data中数据更改newData同样会变
            heap = newData;
        }
        /// <summary>
        /// 重写输出方法
        /// </summary>
        /// <returns></returns>
        public override string ToString()
        {
            StringBuilder stringBuilder = new StringBuilder();
            stringBuilder.Append("[");
            for (int i = 1; i <=N; i++)
            {
                stringBuilder.Append(heap[i]);
                if (i != N)
                    stringBuilder.Append(",");
            }
            stringBuilder.Append("]");
            return stringBuilder.ToString();
        }




    }
}

 调用：

按照二叉堆最大堆的定义，实现结果应为：

  class Program
    {
        static void Main(string[] args)
        {  
            MaxHeap<int> maxHeap = new MaxHeap<int>(); 
            int[] arr = { 3,2,1,5,4};  
            for (int i = 0; i < arr.Length; i++)
            {
                maxHeap.Insert(arr[i]);
                Console.WriteLine(maxHeap);
            }

            maxHeap.RemoveMax(); 
            Console.WriteLine(maxHeap);

        }
    }

结果：

[3]
[3,2]
[3,2,1]
[5,3,1,2]
[5,4,1,2,3]
[4,3,1,2]

 和预期一致。

最小堆

 最小堆任何一个父节点的值，都小于等于它左右孩子节点的值。

堆排序

 堆排序是利用堆这种数据结构而设计的一种排序算法，堆排序是一种选择排序，它的最坏，最好，平均时间复杂度均为O(nlogn)，它也是不稳定排序。堆排序的基本思想是：将待排序序列构造成一个大顶堆，此时，整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换，此时末尾就为最大值。然后将剩余n-1个元素重新构造成一个堆，这样会得到n个元素的次小值。如此反复执行，便能得到一个有序序列了（一般升序采用大顶堆，降序采用小顶堆)。

代码如下：

    class HeapSort1
    {
        public static void Sort(int[] arr)
        {
            int n = arr.Length;
            MaxHeap<int> maxHeap = new MaxHeap<int>(n);
            for (int i = 0; i < n; i++)
            {
                maxHeap.Insert(arr[i]);
            }
            //要想实现正序，那么最大值就是放后面，所以i--；
            for (int i = n - 1; i >= 0; i--)
            {
                arr[i] = maxHeap.RemoveMax();
            }  
        } 
    }

但是，当前代码的性能不是很好，他的时间复杂度：建堆(nlogn)+出堆(nlogn)=O(2nlogn)，空间复杂度为O(n)

可以使用原地堆排序进行优化。

原地堆排序

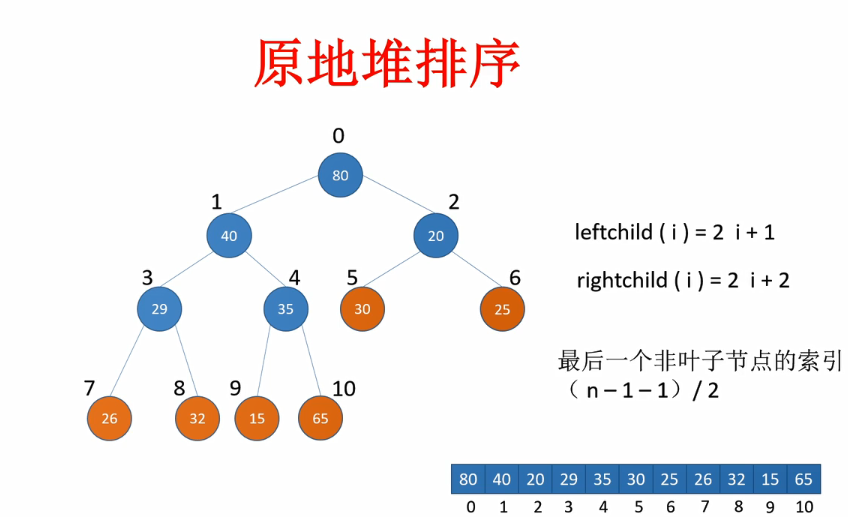
如下图，符合完全二叉树，但是不符合最大堆定义。 图中的橙色节点都是叶子节点，我们可以从第一个非叶子节点开始进行考察，其中n代表数组的个数。

 

class HeapSort2
    {
        public static void Sort(int[] arr)
        {
            int n = arr.Length;
            MaxHeap<int> maxHeap = new MaxHeap<int>(n);
            for (int i = 0; i < n; i++)
            {
                maxHeap.Insert(arr[i]);
            }
            //因为要从第一个非叶子节点开始，并且期间需要元素下沉来实现最大堆。
            for (int i = (n - 1 - 1) / 2; i >= 0; i--)
            {
                Sink(arr, i, n - 1);
            }
            //原地堆排序
            for (int i = n - 1; i >= 0; i--)
            {
                //交换元素
                Swap(arr, 0, i); 
                //交换之后再次比较
                Sink(arr, 0, i - 1); 
            } 
        }

        /// <summary>
        /// 元素下沉
        /// </summary>
        /// <param name="k"></param>
        private static void Sink(int[] arr, int k, int N)
        {
            //当前存在孩子节点的时候才能往下比较
            while (2 * k + 1 <= N)
            {
                int j = 2 * k + 1;
                //j+1<=N表示存在右孩子节点，
                //如果存在右孩子节点，并且右孩子节点比左孩子节点大
                if (j + 1 <= N && arr[j + 1].CompareTo(arr[j]) > 0)
                {
                    //右孩子的位置
                    j++;
                }
                //如果当前节点大于右孩子节点，则跳出
                if (arr[k].CompareTo(arr[j]) >= 0)
                {
                    break;
                }

                Swap(arr, k, j);
                //j代表交换完成之后元素所在的新的位置，赋给k，看看这个位置是否需要继续交换
                k = j;
            }

        }
        private static void Swap(int[] arr, int i, int j)
        {
            int e = arr[i];
            arr[i] = arr[j];
            arr[j] = e;
        }


    }

优先队列

基于最大堆实现最大优先队列

完整代码：

最大最小数组堆：

namespace DataStructure
{
    /// <summary>
    /// 最大数组堆
    /// </summary>
    /// <typeparam name="E"></typeparam>
    class MaxHeap<E> where E : IComparable<E>
    {

        private E[] heap;
        private int N;
        public MaxHeap(int capacity)
        {
            //之所以加1，是因为索引为0的地方是没有存值的。
            heap = new E[capacity + 1];
            N = 0;
        }

        public MaxHeap() : this(10)
        {
        }
        public int Count { get { return N; } }
        public bool IsEmpty { get { return N == 0; } }

        public void Insert(E e)
        {
            //之所以减一，是因为二叉堆中的具体数是在索引1处开始。
            if (N == heap.Length - 1)
            {
                ResetCapacity(heap.Length * 2);
            }

            //首先保证此树是完全二叉树。
            heap[N + 1] = e;
            N++;
            Swim(N);
        }
        /// <summary>
        /// 元素上游
        /// </summary>
        /// <param name="k"></param>
        private void Swim(int k)
        {
            //k==1时代表找到了根节点，所以不用再比较了，不能上游了
            while (k > 1 && heap[k].CompareTo(heap[k / 2]) > 0)
            {
                Swap(k, k / 2);
                k = k / 2;
            }

        }

        private void Swap(int i, int j)
        {
            E e = heap[i];
            heap[i] = heap[j];
            heap[j] = e;
        }
        //删除最大元素
        public E RemoveMax()
        {
            if (IsEmpty)
                throw new Exception("堆为空");
            Swap(1, N);
            E max = heap[N];
            //设置默认值，让垃圾回收器GC进行回收。
            heap[N] = default;
            N--;
            Sink(1);
            if (N == (heap.Length - 1) / 4)
                ResetCapacity(heap.Length / 2);
            return max;
        }
        /// <summary>
        ///返回最大值
        /// </summary>
        /// <returns></returns>
        public E Max()
        {
            if (IsEmpty)
                throw new Exception("堆为空");
            return heap[1];
        }

        /// <summary>
        /// 元素下沉
        /// </summary>
        /// <param name="k"></param>
        private void Sink(int k)
        {
            //当前存在孩子节点的时候才能往下比较
            while (2 * k <= N)
            {
                int j = 2 * k;
                //j+1<=N表示存在右孩子节点，
                //如果存在右孩子节点，并且右孩子节点比左孩子节点大
                if (j + 1 <= N && heap[j + 1].CompareTo(heap[j]) > 0)
                {
                    //右孩子的位置
                    j++;
                }
                //如果当前节点大于右孩子节点，则跳出
                if (heap[k].CompareTo(heap[j]) >= 0)
                {
                    break;
                }

                Swap(k, j);
                //j代表交换完成之后元素所在的新的位置，赋给k，看看这个位置是否需要继续交换
                k = j;
            }

        }

        /// <summary>
        /// 数组扩容
        /// </summary>
        /// <param name="newLength"></param>
        private void ResetCapacity(int newLength)
        {
            E[] newData = new E[newLength];
            //将旧有数据复制到扩容后的新数组中
            heap.CopyTo(newData, 0);
            //赋值给原有数组 注意此时给data的是引用，data中数据更改newData同样会变
            heap = newData;
        }
        /// <summary>
        /// 重写输出方法
        /// </summary>
        /// <returns></returns>
        public override string ToString()
        {
            StringBuilder stringBuilder = new StringBuilder();
            stringBuilder.Append("[");
            for (int i = 1; i <= N; i++)
            {
                stringBuilder.Append(heap[i]);
                if (i != N)
                    stringBuilder.Append(",");
            }
            stringBuilder.Append("]");
            return stringBuilder.ToString();
        }




    }
     
    /// <summary>
    /// 最小数组堆
    /// </summary>
    /// <typeparam name="E"></typeparam>
    class MinHeap<E> where E : IComparable<E>
    {

        private E[] heap;
        private int N;
        public MinHeap(int capacity)
        {
            //之所以加1，是因为索引为0的地方是没有存值的。
            heap = new E[capacity + 1];
            N = 0;
        }

        public MinHeap() : this(10)
        {
        }
        public int Count { get { return N; } }
        public bool IsEmpty { get { return N == 0; } }

        public void Insert(E e)
        {
            //之所以减一，是因为二叉堆中的具体数是在索引1处开始。
            if (N == heap.Length - 1)
            {
                ResetCapacity(heap.Length * 2);
            }

            //首先保证此树是完全二叉树。
            heap[N + 1] = e;
            N++;
            Swim(N);
        }
        /// <summary>
        /// 元素上游
        /// </summary>
        /// <param name="k"></param>
        private void Swim(int k)
        {
            //k==1时代表找到了根节点，所以不用再比较了，不能上游了
            while (k > 1 && heap[k].CompareTo(heap[k / 2]) < 0)
            {
                Swap(k, k / 2);
                k = k / 2;
            }

        }

        private void Swap(int i, int j)
        {
            E e = heap[i];
            heap[i] = heap[j];
            heap[j] = e;
        }
        //删除最小元素
        public E RemoveMin()
        {
            if (IsEmpty)
                throw new Exception("堆为空");
            Swap(1, N);
            E max = heap[N];
            //设置默认值，让垃圾回收器GC进行回收。
            heap[N] = default;
            N--;
            Sink(1);
            if (N == (heap.Length - 1) / 4)
                ResetCapacity(heap.Length / 2);
            return max;
        }
        /// <summary>
        ///返回最小值
        /// </summary>
        /// <returns></returns>
        public E Min()
        {
            if (IsEmpty)
                throw new Exception("堆为空");
            return heap[1];
        }

        /// <summary>
        /// 元素下沉
        /// </summary>
        /// <param name="k"></param>
        private void Sink(int k)
        {
            //当前存在孩子节点的时候才能往下比较
            while (2 * k <= N)
            {
                int j = 2 * k;
                //j+1<=N表示存在右孩子节点，
                //如果存在右孩子节点，并且右孩子节点比左孩子节点小
                if (j + 1 <= N && heap[j + 1].CompareTo(heap[j]) < 0)
                {
                    //右孩子的位置
                    j++;
                }
                //如果当前节点小于右孩子节点，则跳出
                if (heap[k].CompareTo(heap[j]) <= 0)
                {
                    break;
                }

                Swap(k, j);
                //j代表交换完成之后元素所在的新的位置，赋给k，看看这个位置是否需要继续交换
                k = j;
            }

        }

        /// <summary>
        /// 数组扩容
        /// </summary>
        /// <param name="newLength"></param>
        private void ResetCapacity(int newLength)
        {
            E[] newData = new E[newLength];
            //将旧有数据复制到扩容后的新数组中
            heap.CopyTo(newData, 0);
            //赋值给原有数组 注意此时给data的是引用，data中数据更改newData同样会变
            heap = newData;
        }
        /// <summary>
        /// 重写输出方法
        /// </summary>
        /// <returns></returns>
        public override string ToString()
        {
            StringBuilder stringBuilder = new StringBuilder();
            stringBuilder.Append("[");
            for (int i = 1; i <= N; i++)
            {
                stringBuilder.Append(heap[i]);
                if (i != N)
                    stringBuilder.Append(",");
            }
            stringBuilder.Append("]");
            return stringBuilder.ToString();
        }
 
    }
}

最大最小优先队列：

namespace DataStructure
{
    /// <summary>
    /// 最大优先队列  IQueue：是自定义的一个接口
    /// </summary>
    /// <typeparam name="E"></typeparam>
    class MaxPQ<E> : IQueue<E> where E : IComparable<E>
    {
        private MaxHeap<E> heap;

        public int Count { get { return heap.Count; } }

        public bool IsEmpty { get { return heap.IsEmpty; } }

        public MaxPQ(int capacity)
        {
            heap = new MaxHeap<E>(capacity);
        }
        public MaxPQ()
        {
            heap = new MaxHeap<E>();
        }

        public void Enqueue(E e)
        {
            heap.Insert(e);
        }

        public E Dequeue()
        {
            return heap.RemoveMax();
        }

        public E Peek()
        {
            return heap.Max();
        }
    }

    /// <summary>
    /// 最小优先队列  
    /// </summary>
    /// <typeparam name="E"></typeparam>
    class MinPQ<E> : IQueue<E> where E : IComparable<E>
    {
        private MinHeap<E> heap;

        public int Count { get { return heap.Count; } }

        public bool IsEmpty { get { return heap.IsEmpty; } }

        public MinPQ(int capacity)
        {
            heap = new MinHeap<E>(capacity);
        }
        public MinPQ()
        {
            heap = new MinHeap<E>();
        }

        public void Enqueue(E e)
        {
            heap.Insert(e);
        }

        public E Dequeue()
        {
            return heap.RemoveMin();
        }

        public E Peek()
        {
            return heap.Min();
        }
    }
}

（1）在一百万个元素中找出前10个最小的元素。

最好用优先队列，因为其他那些排序方法需要把1百万个数据先放到内存中才能进行排序，通过优先队列，来一个数据，就处理一个，不需要那么多的内存，只需要开辟10个内存来储存即可。

我们可以把数据规模缩小来进行测试，如下：

我们可以先找出3个元素，然后将剩余的元素和选出来的元素进行比较，如果存在比这3个元素小的，则替换，否则继续比较。

   class Program
    {

        static void Main(string[] args)
        {
            //找最小的三个数
            MaxPQ<int> maxHeap = new MaxPQ<int>(3);
            int[] arr = { 3, 2, 1, 5, 4 };
            for (int i = 0; i < arr.Length; i++)
            {
                if (maxHeap.Count < 3)
                {
                    maxHeap.Enqueue(arr[i]);
                }
                //如果当前数比最大数还小，则去除最大数，
                else if (arr[i] < maxHeap.Peek())
                {
                    //去除队列中最大的数
                    maxHeap.Dequeue();
                    maxHeap.Enqueue(arr[i]);
                }

            }

        }
    }