题目大意:有两类武器(主武器和副武器),每类有若干把,每把武器都有一个基础属性S,以及k个附加属性,让你选一把主武器M和一把副武器S,使得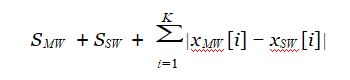 最大。
最大。
显然后面的和式是一个k维的曼哈顿距离,带绝对值符号不好算,因此要想办法把绝对值去掉。由于两点任意一个维度(设其值分别为a,b)的曼哈顿距离要么是a-b,要么是b-a,符号总是相反的,因此可以二进制枚举每一维的正负号,对主武器取最大值,对副武器取最小值,两者相减就可以得到最大的曼哈顿距离。中间可能有的值不合法,但不合法的值一定不是最优值,因此可以忽略。
至于基础属性,只要对主武器加上S,对副武器减去S就行了。
1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 const int N=1e5+10,inf=0x3f3f3f3f3f3f3f3fll; 5 int n,m,k,a[N][6],b[N][6],Log[N]; 6 ll Sa[N][1<<5],Sb[N][1<<5]; 7 int main() { 8 Log[0]=-1; 9 for(int i=1; i<N; ++i)Log[i]=Log[i>>1]+1; 10 int T; 11 for(scanf("%d",&T); T--;) { 12 scanf("%d%d%d",&n,&m,&k); 13 for(int i=0; i<n; ++i) { 14 scanf("%d",&a[i][k]); 15 for(int j=0; j<k; ++j)scanf("%d",&a[i][j]); 16 } 17 for(int i=0; i<m; ++i) { 18 scanf("%d",&b[i][k]); 19 for(int j=0; j<k; ++j)scanf("%d",&b[i][j]); 20 } 21 for(int i=0; i<n; ++i) { 22 for(int S=0; S<(1<<k); ++S)Sa[i][S]=0; 23 for(int j=0; j<k; ++j)Sa[i][0]+=a[i][j]; 24 Sa[i][0]+=a[i][k]; 25 } 26 for(int i=0; i<m; ++i) { 27 for(int S=0; S<(1<<k); ++S)Sb[i][S]=0; 28 for(int j=0; j<k; ++j)Sb[i][0]+=b[i][j]; 29 Sb[i][0]-=b[i][k]; 30 } 31 for(int S=1; S<(1<<k); ++S) { 32 for(int i=0; i<n; ++i)Sa[i][S]=Sa[i][S^(1<<Log[S])]-2*a[i][Log[S]]; 33 for(int i=0; i<m; ++i)Sb[i][S]=Sb[i][S^(1<<Log[S])]-2*b[i][Log[S]]; 34 } 35 ll ans=0; 36 for(int S=0; S<(1<<k); ++S) { 37 ll mx=~inf,mi=inf; 38 for(int i=0; i<n; ++i)mx=max(mx,Sa[i][S]); 39 for(int i=0; i<m; ++i)mi=min(mi,Sb[i][S]); 40 ans=max(ans,mx-mi); 41 } 42 printf("%lld ",ans); 43 } 44 return 0; 45 }