1 class Solution { 2 public int maximalRectangle(char[][] matrix) { 3 if(matrix == null || matrix.length == 0 || matrix[0].length == 0) return 0; 4 5 int[] height = new int[matrix[0].length]; 6 for(int i = 0; i < matrix[0].length; i ++){ 7 if(matrix[0][i] == '1') height[i] = 1; 8 } 9 int result = largestInLine(height); 10 for(int i = 1; i < matrix.length; i ++){ 11 resetHeight(matrix, height, i); 12 result = Math.max(result, largestInLine(height)); 13 } 14 15 return result; 16 } 17 18 private void resetHeight(char[][] matrix, int[] height, int idx){ 19 for(int i = 0; i < matrix[0].length; i ++){ 20 if(matrix[idx][i] == '1') height[i] += 1; 21 else height[i] = 0; 22 } 23 } 24 25 public int largestInLine(int[] height) { 26 if(height == null || height.length == 0) return 0; 27 int len = height.length; 28 Stack<Integer> s = new Stack<Integer>(); 29 int maxArea = 0; 30 for(int i = 0; i <= len; i++){ 31 int h = (i == len ? 0 : height[i]); 32 if(s.isEmpty() || h >= height[s.peek()]){ 33 s.push(i); 34 }else{ 35 int tp = s.pop(); 36 maxArea = Math.max(maxArea, height[tp] * (s.isEmpty() ? i : i - 1 - s.peek())); 37 i--; 38 } 39 } 40 return maxArea; 41 } 42 }
补充一个python的实现:
1 class Solution: 2 def maximalRectangle(self, matrix: 'List[List[str]]') -> int: 3 if matrix == None: 4 return 0 5 row = len(matrix) 6 if row == 0: 7 return 0 8 column = len(matrix[0]) 9 if column == 0: 10 return 0 11 heights = [0] * column 12 for i in range(column): 13 if matrix[0][i] == '1': 14 heights[i] = 1 15 result = self.largestRectangleArea(heights) 16 for i in range(1,row): 17 self.resetHeight(matrix,heights,i) 18 result = max(result,self.largestRectangleArea(heights)) 19 return result 20 21 def largestRectangleArea(self, heights: 'List[int]') -> int: 22 heights.append(0)#默认最后补充一个0,方便统一处理 23 n = len(heights) 24 s = [] 25 max_area = 0#最大面积 26 tp = 0#栈顶索引 27 area_with_top = 0#临时面积 28 i = 0 29 while i < n: 30 if len(s) == 0 or heights[s[-1]] <= heights[i]: 31 s.append(i)#栈内记录的是高度递增的索引 32 i += 1 33 else:#遇到了高度比当前栈顶元素低的元素时, 34 tp = s.pop(-1)#清算栈内的元素的高度 35 if len(s) == 0: 36 area_with_top = heights[tp] * i#栈内没有元素,则宽度是i 37 else:#高度是栈顶元素,宽度是i - 1 - 前一个栈顶元素的索引 38 area_with_top = heights[tp] * (i - s[-1] - 1) 39 max_area = max(max_area,area_with_top)#更新最大值 40 return max_area 41 42 def resetHeight(self,matrix,height,idx): 43 for i in range(len(matrix[0])): 44 if matrix[idx][i] == '1': 45 height[i] += 1 46 else: 47 height[i] = 0
思路分析:本题以leetcode 84为基础,相当于计算一个柱状图中最大的面积。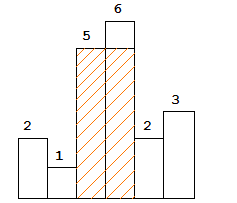
如图上所示,对于数组[2,1,5,6,2,3]其最大面积是10。在此基础上,将本题转化为row次的柱状图计算:
 按照行“递增”计算4次。
按照行“递增”计算4次。
1、 [1,0,1,0,0],最大面积是1
[1,0,1,0,0],最大面积是1
2、 [1+1,0,1+1,1,1] => [2,0,2,1,1],最大面积是3
[1+1,0,1+1,1,1] => [2,0,2,1,1],最大面积是3
3、 [1+1+1,1,1+1+1,1+1,1+1] => [3,1,3,2,2],最大面积是6
[1+1+1,1,1+1+1,1+1,1+1] => [3,1,3,2,2],最大面积是6
4、 [1+1+1+1,0,0,1+1+1,0] => [4,0,0,3,0],最大面积是4
[1+1+1+1,0,0,1+1+1,0] => [4,0,0,3,0],最大面积是4
经过这4次循环,计算完毕。第3次得到的结果,是这个二维数组可构成的最大面积6。