一次线性回归分析详解及推导

线性回归 linear regression

我们需要根据一个人的工作年限 来预测他的 薪酬 （我们假设一个人的薪酬只要工作年限有关系）。

首先引入必要的类库，并且获得trainning data。

import tensorflow as tf
import pandas as pd
import numpy as np

unrate = pd.read_csv('SD.csv')
print(unrate)

    Year  Salary
0    1.0   39451
1    1.2   46313
2    1.4   37839
3    1.9   43633
4    2.1   39999
..   ...     ...
85  12.0  106247
86  12.5  117634
87  12.6  113300
88  13.3  123056
89  13.5  122537

[90 rows x 2 columns]

接着，我们用matplotlib绘制出工作年限和薪酬之间的关系的点状图，方便我们更加直观的感受他们之间的关系。

from matplotlib import pyplot as plt

unrate = unrate.sort_values('Year')

plt.scatter(unrate['Year'],unrate['Salary'])

plt.show()

根据上图的关系，我们可以看到：他们基本上还是成正相关的。考虑到只有一维数据，我们假定存在一个函数，可以描述工作年限和薪酬之间的关系。我们假定该函数为：$$ hat{y} = Wx+b $$

$ hat{y} $即为我们根据模型预测出来的数值。 $ hat(y) $ 和实际数值y 之间的距离，即为我们预测的偏差值。即：$$ loss = sum_{i=0}^{n} (y_i- hat y_i)^2$$

</p>

我们先随机的挑选W 和b ，并且计算一下loss。同时绘制出来预测的数值与原来的数值。

w = np.random.rand(1)
b = np.random.rand(1)

y_pred = (unrate['Year']*w + b)
loss = np.power((unrate['Year']*w + b)-unrate['Salary'],2).sum()

plt.scatter(unrate['Year'],unrate['Salary'])
plt.plot(unrate['Year'],y_pred)
plt.show()
print(w)
print(b)
print(loss)

[0.31944837]
[0.48968515]
698967170603.215

我们可以看到差距还是比较大的。

那么该怎么求w和b呢？

而我们工作的本质上就在寻找合适的W和b，从而达到loss最小。也就是找 $ loss = sum_{i=0}^{n} (y_i- hat y_i)^2$的最小值。

单纯的从数学上来看。寻找一个函数的极值，就是找到它导数为0的驻点，然后去判断哪些驻点为最小值。


我们把 $ hat(y)$的计算公式带入 loss中，我们得到

[loss = sum_{i=0}^{n} (y_i-Wx-b)^2 ]

我们对这个函数求导函数得到

[frac{dl}{dw}=frac{dl}{dhat{y}}*frac{dhat{y}}{dw} ]

[frac{dl}{dw}=-2sum_{i=0}^{n}((y_i-hat{y}_i)*frac{dhat{y}}{dw}) = -2sum_{i=0}^{n}((y_i-hat{y}_i)x_i) ]

[frac{dl}{db} = -2sum_{i=0}^{n}(frac{dl}{dhat{y}_i}* frac{dhat{y}_i}{db})=-2sum_{i=0}^{n}(y_i-hat{y}_i) ]

如果直接这样解方程，求出最小值，当然也可以，但是通用性不够。所以用了另外一种方式：叫做梯度下降的方式去求解。

关于梯度下降，我后面再进行探讨和学习，现在只是简单的理解其中的含义。

简单的理解，就是在一个凸函数中，随机的选择一个点，然后算出这个点的斜率，然后让这个点减去斜率*一个速率，然后这个点就会向着最低点移动，直到到达最低点的时候，斜率=0，所以便不再变化。这样的话，我们得到一个通用的办法，就不用解方程了，任何函数，只要我们得到他的导函数，然后随机一个点，重复梯度下降的步骤，就可以得到最合适的数值。

def train(w, b):
    learning_rate = 0.0001

    dw = np.sum((np.power(unrate['Year'],2)* w -np.transpose(unrate['Salary']-b)*unrate['Year']))
    db = np.sum(unrate['Salary']-(unrate['Year']*w-b))

    temp_w = w - learning_rate * dw
    temp_b = b - learning_rate * db
    w = temp_w
    b = temp_b
    return w, b

我们先来train一次，看看效果

w,b = train(w,b)

y_pred = (unrate['Year']*w + b)
loss = np.power((unrate['Year']*w + b)-unrate['Salary'],2).sum()

plt.scatter(unrate['Year'],unrate['Salary'])
plt.plot(unrate['Year'],y_pred)
plt.show()
print(w)
print(b)
print(loss)

[5430.27093385]
[-755.1422668]
246914588144.68262

看到有明显的效果，我们来多尝试几次试试

for i in range(1000):
    w,b = train(w,b)

y_pred = (unrate['Year']*w + b)
loss = np.power((unrate['Year']*w + b)-unrate['Salary'],2).sum()

plt.scatter(unrate['Year'],unrate['Salary'])
plt.plot(unrate['Year'],y_pred)
plt.show()
print(w)
print(b)
print(loss)

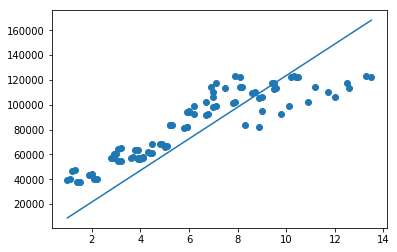
[12742.12454444]
[-3940.07990295]
39663899737.785065

我们可以看到已经拟合出来一条直线，基本拟合了训练的数据，这个时候，给定一个x值，我们都可以预测一个(hat{y})

x = 20
y_hat = w*x+b
print(y_hat)

[250902.4109859]

但是从图中，我们可以看出来，拟合出来的直线，很明显不能非常完美的贴合所有的数据。可能这些数据的分布，不是呈简单线性相关。有可能是一个曲线或者抛物线的形式。随后，我讲尝试进行多元的拟合。