POJ 2488-A Knight's Journey（DFS）

A Knight's Journey

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 31702		Accepted: 10813

Description

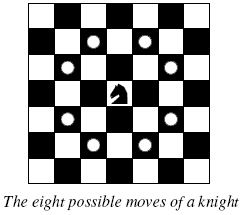Background 
The knight is getting bored of seeing the same black and white squares again and again and has decided to make a journey 
around the world. Whenever a knight moves, it is two squares in one direction and one square perpendicular to this. The world of a knight is the chessboard he is living on. Our knight lives on a chessboard that has a smaller area than a regular 8 * 8 board, but it is still rectangular. Can you help this adventurous knight to make travel plans?

 

Problem 
Find a path such that the knight visits every square once. The knight can start and end on any square of the board.

Input

The input begins with a positive integer n in the first line. The following lines contain n test cases. Each test case consists of a single line with two positive integers p and q, such that 1 <= p * q <= 26. This represents a p * q chessboard, where p describes how many different square numbers 1, . . . , p exist, q describes how many different square letters exist. These are the first q letters of the Latin alphabet: A, . . .

Output

The output for every scenario begins with a line containing "Scenario #i:", where i is the number of the scenario starting at 1. Then print a single line containing the lexicographically first path that visits all squares of the chessboard with knight moves followed by an empty line. The path should be given on a single line by concatenating the names of the visited squares. Each square name consists of a capital letter followed by a number. 
If no such path exist, you should output impossible on a single line.

Sample Input

3
1 1
2 3
4 3

Sample Output

Scenario #1:
A1

Scenario #2:
impossible

Scenario #3:
A1B3C1A2B4C2A3B1C3A4B2C4

题意：国际象棋。然后给一个马（马走日） ，能够从随意点出发，找一条能够訪问全部格子（p*q的棋盘）的路径，注意路径假设有多条要求输出字典序最小的那条。
。
然后这个能够搜索的时候按字典序搜。
。
就是搜索方向要固定。。不能随意写了

然后其它的没什么了 直接深搜。搜到答案之后直接return ；

#include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdlib>
#include <string>
#include <cctype>
#include <vector>
#include <cstdio>
#include <cmath>
#include <deque>
#include <stack>
#include <map>
#include <set>
#define ll long long
#define maxn 116
#define pp pair<int,int>
#define INF 0x3f3f3f3f
#define max(x,y) ( ((x) > (y)) ? (x) : (y) )
#define min(x,y) ( ((x) > (y)) ? (y) : (x) )
using namespace std;
int n,m,k,ans,dir[8][2]={{-1,-2},{1,-2},{-2,-1},{2,-1},{-2,1},{2,1},{-1,2},{1,2}};
bool vis[27][27];
int sx[30],sy[30],top,ok;
void dfs(int x,int y)
{
	if(ok) return ;
	if(top==n*m)
	{
		ok=1;
		for(int i=0;i<top;i++)
		printf("%c%d",'A'+sy[i]-1,sx[i]);
		return ;
	}
	for(int i=0;i<8;i++)
	{
		int tx=x+dir[i][0];
		int ty=y+dir[i][1];
		if(tx>=1&&tx<=n&&ty>=1&&ty<=m&&!vis[tx][ty])
		{
			vis[tx][ty]=1;sx[top]=tx;sy[top++]=ty;
			dfs(tx,ty);
			vis[tx][ty]=0;top--;
		}
	}
}
int main()
{
	int T,cas=1;
	scanf("%d",&T);
    while(T--)
	{
		scanf("%d%d",&n,&m);ok=0;
		printf("Scenario #%d:
",cas++);
		memset(vis,0,sizeof(vis));top=0;
		vis[1][1]=1;sx[top]=1;sy[top++]=1;
		dfs(1,1);
		if(!ok)
			printf("impossible");
		puts("");if(T)puts("");
	}
	return 0;
}