直角坐标是常用的坐标法,但是对于一些特别的问题,在直角坐标系下处理就显得有点笨拙了。这个时候,不妨试试极坐标。它可以使得问题变得出乎意料的简洁,也能让问题直观和清晰起来。
极坐标
什么是极坐标
概念来自百度百科:
在平面内取一个定点O,叫极点,引一条射线Ox,叫做极轴,再选定一个长度单位和角度的正方向(通常取逆时针方向)。对于平面内任何一点M,用r表示线段OM的长度,θ表示从Ox到OM的角度,r叫做点M的极径,θ叫做点M的极角,有序数对 (r,θ)就叫点M的极坐标,这样建立的坐标系叫做极坐标系。通常情况下,M的极径坐标单位为1(长度单位),极角坐标单位为rad(或°)。
简单地说,极坐标有两个主要部分:长度和方向。
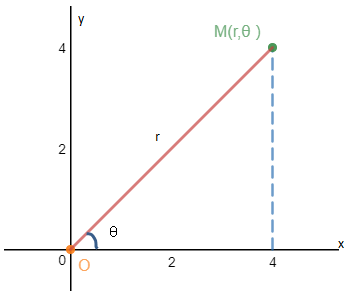
极坐标仅仅是将直角坐标系的点换了一个表示法,仍未脱离原来的直角坐标系。很容易知道,如果M用x和y表示,那么:
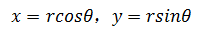
这就是直角坐标系转换为极坐标表示法的转换公式。此外:
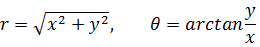
实际上距离和夹角都可能是负数,这种写法可以避免和正负号搅合在一起。
注:在极坐标中,x不再是y的函数,即x不再是变量,这在上篇文章的“新的思维模式”一节做过详细说明。
极坐标下的点、直线和圆
点
现在尝试将(x, y) = (1, -1)转换为极坐标表示法:
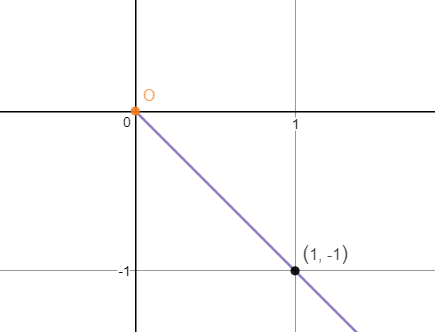
根据转换公式,可以得到三组答案:

直线
用极坐标表示直线y = 1。
y = rsinθ=1, r = 1/sinθ
这就是结果。这可以用下图表示:
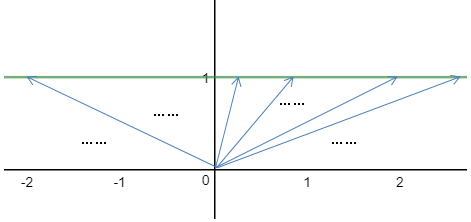
图中每个向量长度都表示r,与x轴的夹角是θ,r = 1/sinθ呈扇形展开,因此也可以知道θ的取值范围是0 ≤ θ ≤ π
圆
在直角坐标系下,半径为a的圆是x2 + y2 = a2,转换为极坐标后:
所以可以用r = a表示极坐标系下的圆,当r的取值范围是(-∞, +∞)时,表示极坐标系下的所有点。
r = 1
示例
用极坐标表示(x – a)2 + y2 = a2
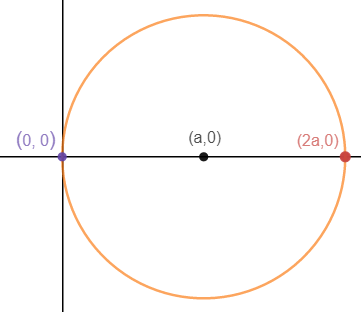
圆心并不在原点。我们可以直接套用公式:
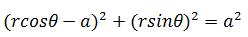
也可以使用一个比较快的方法,先计算,后代入:
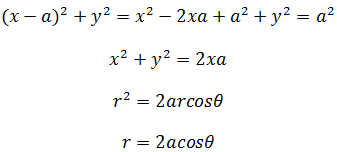
还剩下最后一点,θ的取值范围,少了这点,我们就无法对其进行积分。
当θ = 0时,r的一端在(2a, 0)点;点沿着圆逆时针转动,当θ= π/2时点在(0, 0)处,期间r扫过了上半圆:
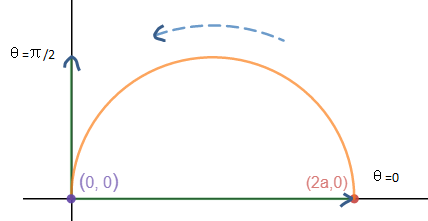
同理,当-π/2 <=θ<=0时,r扫过了下半圆。因此,θ的取值范围是[-π/2, π/2]
极坐标下的面积
面积公式

如上图所示,在已知半径和夹角的情况下很容易求得扇形的面积。
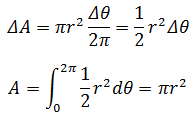
如果是一个不规则曲线形成的面积呢?
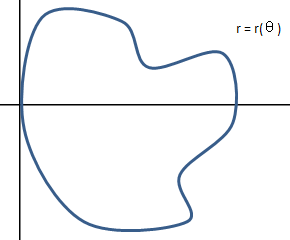
A = ?
我们可以利用黎曼和的知识对其进行切分,形成一个个小扇形:

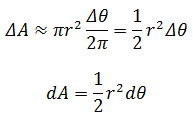
曲线内的任意扇形:
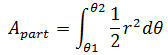
整个面积:
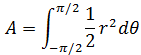
这也是极坐标下的面积公式。
示例1
计算r = 2acosθ的面积。
这在上一节的示例中出现过,如果过退化为直角坐标系,很容易看出是一个圆,其面积是:

这正是期待的结果。
示例2
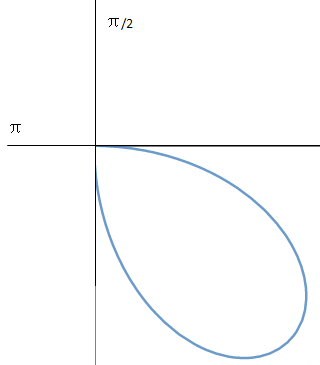
r = sin2θ的面积
为了更直观地计算面积,首先要画图。
相面是θ在第一象限内的取值:
θ = 0, r = 0; θ = π/4, r = 1; θ = π/2, r = 0。
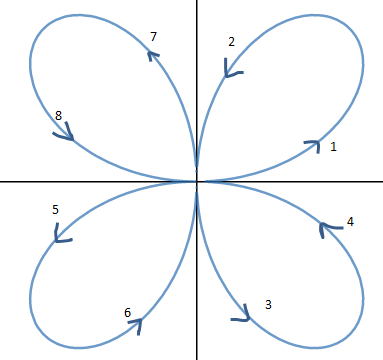
π/2是一个周期,四个象限的图形应当一致:
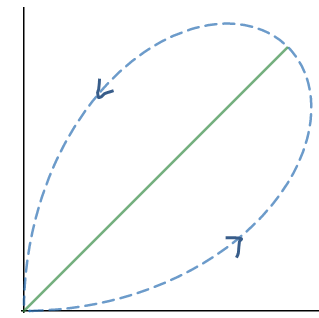
实际上这就是著名的四叶玫瑰函数,它的运动轨迹如下:
当π/2 ≤ θ ≤ π时,曲线向相反方向运动:
现在可以计算面积了。
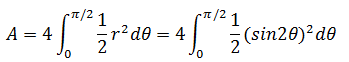
出处:微信公众号 "我是8位的"
本文以学习、研究和分享为主,如需转载,请联系本人,标明作者和出处,非商业用途!
扫描二维码关注作者公众号“我是8位的”
