Java 算法 - 跳表:为什么 Redis 一定要用跳表来实现有序集合?
数据结构与算法之美目录(https://www.cnblogs.com/binarylei/p/10115867.html)
推荐文章:
在二分法查找一文中,我们知道二分法查找一种非常高效的算法,其时间复杂度是 O(logn)。但如果直接使用链表进行二分法查找,时间复杂度就上升为 O(n),甚至比链表顺序访问还要高。下面介绍一种基于链表的二分法查找 - 跳表。
跳表是由 William Pugh 发明的,最早出现于他在1990 年发表的论文 《Skip Lists: A Probabilistic Alternative to Balanced Trees》。对细节感兴趣的同学可以下载论文原文来阅读。
- 二分法查找:只支持有序的静态数组,不支持动态数据。如果数据需要频繁的插入和删除,那么每次查找时就需要先排序,查找的时间复杂度就上升为 O(nlogn)。
- 跳表:通过构建多级索引,实现链表的二分法查找,支持动态数据。
跳表使用空间换时间的设计思路,通过构建多级索引来提高查询的效率,实现了基于链表的“二分查找”。跳表是一种动态数据结构,支持快速的插入、删除、查找操作,时间复杂度都是 O(logn)。
1. 什么是跳表
在分析跳表结构之前,我们先总结一下目前已经学习的各种数据结构,比较一下它们的优缺点:
| 数据结构 | 时间 | 空间 | 性能影响指标 | 备注 |
|---|---|---|---|---|
| 哈希表 | O(1) | O(n) | 散列函数+散列冲突+负载因子 | 支持动态数据 |
| 有序数组 | O(logn) | O(1) | 查找前必须先排序 | 有序静态数组,不支持动态数据 |
| 二叉查找树 | O(logn) | O(n) | 退化为链表,时间复杂度降为 O(n) | 支持动态数据 |
| 红黑树 | O(logn) | O(n) | 维护树的平衡:左旋右旋 | 支持动态数据 |
| 跳表 | O(logn) | O(n) | 维护索引平衡:随机函数生成索引高度 | 支持动态数据 |
-
哈希表:时间复杂度为 O(1),但无法顺序访问,所以很多场景都 "哈希表" + "链表" 一起组合使用。
-
有序数组:通过二分法查找时间复杂度是 O(logn),非常高效。但它要求必须是静态的有序数组,如果是动态数据,每次查找前还需要排序,则时间复杂度退化成 O(nlogn)。因此,它的适用场景是一次排序,多次查找的静态数据。
-
二叉查找树:二叉查找树支持动态数据,但如果退化为链表,其时间复杂度也降为 O(n)。因此,平衡二叉查找树诞生了,但实现严格的平衡(树的左右高度差不能大于 1),代价也太大。
-
红黑树:红黑树是平衡二叉查找树的升级版,它不再追求绝对平衡,只追求相对平衡。它保证任意一个叶子结点的最大路径不能大于 2 倍的最小路径,也就是树的高度最大为 2logn。因此,时间复杂度稳定在 O(logn),但为了维护树的相对平衡,实现过程还是很复杂。
-
跳表:Redis 就是选择跳表实现有序集合。链表之所以不能使用二分法查找,是因为查找中间结点需要遍历链表,时间复杂度是 O(n)。但如果我们直接缓存索引,将查找中间结点的时间复杂度降为 O(1)。这样跳表就可以使用二分法查找,时间复杂度也降为 O(logn)。
跳表相对红黑树,同样支持动态数据,时间复杂度都稳定在 O(logn)。但跳表只需要通过随机函数维护索引平衡,不需要像红黑树那样通过左旋右旋维护树的平衡,代码实现也要相对简单很多。
链表和跳表对比结构图 

思考1:单链表二分法时间复杂度为什么是 O(n)?
链表采用快慢指针算法获取链表的中间节点时,快慢指针都要移动链表长度的一半次,也就是 n / 2 次,总共需要移动 n 次指针才行。
- 第一次,链表长度为 n,需要移动指针 n 次;
- 第二次,链表长度为 n/2,需要移动指针 n/2 次;
- 第三次,链表长度为 n/4,需要移动指针 n/4 次;
- ...
- 以此类推,一直到 1 次为值
- 指针移动的总次数 n + n/2 + n/4 + n/8 + ... + 1 = n(1-0.5)/(1-0.5) = 2n
总结:链表获取中间结点的时间复杂度是 O(2n),不仅远远大于数组二分查找 O(logn),也要大于顺序查找的时间复杂度 O(n)。
2. 跳表工作原理
最理想的跳表如下图所示,严格按照二分法存储索引结构。它的结构类似多层链表,上层索引的数量是下层索引数量的一半,这样查找过程就非常类似于一个二分查找,使得查找的时间复杂度可以降低到 O(logn)。

说明: 上图中包含三级索引,其中头结点是哨兵结点,只存储索引不存储任何数据。查找元素时,需要在逐级索引中依次查找。比如要查找元素 e12,需要通过 L3 -> L2 -> L1 -> L0 依次查找。
(1) 空间复杂度
理想跳表每一层元素都是上一层元素的一半,空间复杂度为 O(n)。
空间复杂度分析:每层索引数 = n/2 + n/4 + n/8 + n/16 + ... + 1 = O(n)
(2)时间复杂度
跳表和二分法查找一样,时间复杂度也是 O(logn)。跳表查找元素时,需要从上到下从左到右,依次遍历索引进行查找:Ln -> Ln-1 ... L1 -> L0(原始链表)。
3. 跳表关键指标
3.1 索引平衡
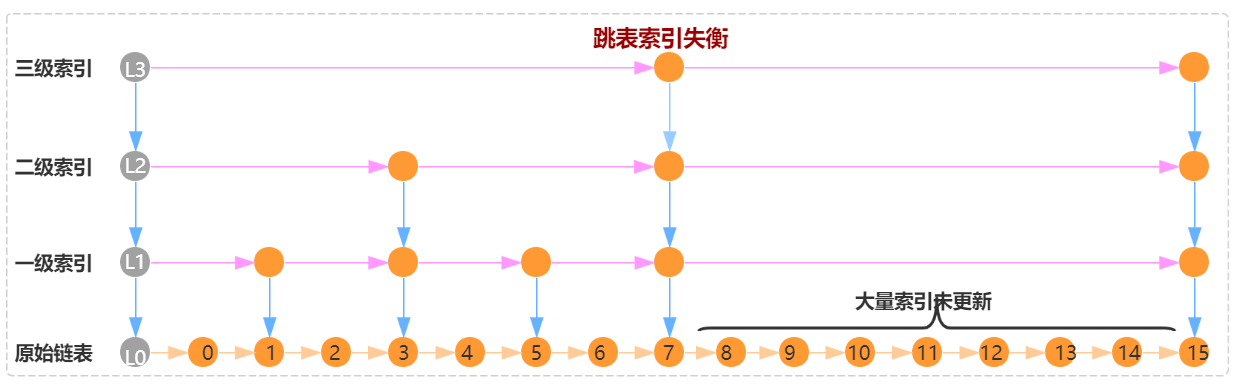
从上述分析,我们可以看出跳表性能好坏,关键在于索引的平衡。如果往跳表中插入大量的数据,而没有更新索引,那么跳表就会退化为链表。同样,如果每次插入删除,都需要维护索引的绝对平衡,会导致大量的索引需要重新平衡,链表的插入删除的时间复杂度为 O(1) 的特性就被破坏了。
- 红黑树:平衡二叉树通过左右旋转,维护树的平衡。在实际软件工程中,因为维护树的绝对平衡代价太大,AVL 树很少使用,反而是红黑树这种只追求相对平衡的二叉查找树经常使用。
- 跳表:同红黑树一样,维护索引的绝对平衡的代价也太大。实现软件工作中,跳表通过随机函数来维护索引的 "平衡性"。
3.2 随机索引
那如何衡量跳表索引的平衡性呢?在《Skip Lists: A Probabilistic Alternative to Balanced Trees》论文中对跳表通过随机函数来维护索引的 "平衡性" 问题进行了详细的说明。
跳表的平衡性关键是由每个节点插入的时候,它的索引层数是由随机函数计算出来的,而且随机的计算不依赖于其它节点,每次插入过程都是完全独立的。这样,就和普通链表的插入一样,查找到插入点位置后,只需要一次操作就可以完成结点插入,时间复杂度为 O(logn)。
随机函数计算索引层数过程如下:
- 首先,每个节点肯定都有第 1 层指针(每个节点都在第 1 层链表里)。
- 如果一个节点有第 i 层( i >= 1)指针(即节点已经在第 1 层到第 i 层链表中),那么它有第(i + 1)层指针的概率为 p。
- 节点最大的层数不允许超过一个最大值,记为 MaxLevel。
randomLevel()
level = 1
// random()返回一个[0...1)的随机数
while random() < p and level < MaxLevel do
level = level + 1
return level
说明: randomLevel() 的伪码中包含两个重要参数:
- 每层指针的概率 p:决定每个结点的平均索引高度。
- 最大索引高度 MaxLevel:决定了跳表的最大数据量,为 2MaxLevel。
在 Redis 的 skiplist 实现中,这两个参数的取值为:
#define ZSKIPLIST_MAXLEVEL 64 /* Should be enough for 2^64 elements */
#define ZSKIPLIST_P 0.25 /* Skiplist P = 1/4 */
3.3 性能分析
跳表的性能分析,我们主要关注两个指标,在概率 p 和最大索引高度 MaxLevel 下,跳表的时间空间复杂度。
- 时间复杂度:用跳表查询到底有多快?时间复杂度是 O(k/p),k 为跳表索引高度。对于 n 个元素的跳表,索引高度为 logn,即跳表查询的时间复杂度是 O(logn/p) = O(logn),p 越小时间复杂度越高。
- 空间复杂度:跳表是不是很浪费内存?空间复杂度是 O(1/(1-p)n) = O(n),p 越小空间复杂度越低。
我们先来计算一下每个节点所包含的平均索引高度。节点包含的索引高度,相当于这个算法在空间上的额外开销(overhead),可以用来度量空间复杂度。
根据前面 randomLevel() 的伪码,我们很容易看出,索引高度越大,概率越低。定量的分析如下:
- 结点层数至少为 1,而大于1的节点层数,满足一个概率分布。
- level=1:表示原始链表,概率为 p1=1 ,元素结点个数 n
- level=2:表示一级索引,概率为 p2=p ,元素结点个数 np^1
- level=3:表示二级索引,概率为 p3=p^2 ,元素结点个数 np^2
...
(1)空间复杂度
因此,一个节点的平均层数(也即包含的平均指针数目),计算如下:
- 1 + p + p2 + p3 + ... + pi-1 = 1/(1-p)
现在很容易计算出每个节点的平均指针层级数(包含原始链表层):
- 当 p = 1/2 时,每个节点所包含的平均指针数目为 2。这是 ConcurrentSkipListMap 的空间复杂度 O(n)。
- 当 p = 1/4 时,每个节点所包含的平均指针数目为 1.33。这是 Redis 中 skiplist 空间复杂度 O(0.33n)。
总结: Redis 中 skiplist 的 p 取值为 0.25,也就是时间复杂度是 O(4n),空间复杂度大概是 O(0.33n)。相对于 Java 中 ConcurrentSkipListMap 的 p 取值为 0.5,Redis 更倾向于时间换空间。
(2)时间复杂度
时间复杂的推算比较复杂,我们只是粗略的估算一下。最主要是知道跳表的时间复杂为 O(logn) 即可。
首先,我们估算一下跳表的索引高度。如果索引有 k 层,第 k 层索引结点的个数为 npk-1 个。当 npk-1 = 1 时表示最大索引高度,则索引高度为 k = log1/pn。忽略 p 这个常量,有 n 个元素的跳表,索引的高度为 logn。
下面,我们使用递归法推导跳表的时间复杂度。跳表查找时,结点的查找是从下往下,从左往右。现在我们反过来,假设从一个层数为 i 的节点 x 出发,需要向左向上攀爬 k 层。这时我们有两种可能:
- 如果节点 x 有第(i + 1)层指针,那么我们需要向上走。这种情况概率为 p。
- 如果节点 x 没有第(i + 1)层指针,那么我们需要向左走。这种情况概率为(1 - p)。
C(0) = 0
C(k) = (1-p)(C(k)+1) + p(C(k-1)+1)
C(k) = k/p = logn/p
说明: 跳表查找的时间复杂度大概为 O(k/p),其中 k 表示跳表索引高度。对于 n 个元素的跳表,其索引高度为 logn,即跳表的时间复杂度为 O(logn)。
4. 跳表操作
- 查找:时间复杂度为 O(logn)。从上至下,从左到右依次遍历。
- 插入:首先需要查找到插入点的位置,将结点插入原始链表中。然后,生成该结点的索引高度,从上至下,依次将索引也插入对应的索引链表中。如插入 e5 时,需要先将 e5 插入原始链表。然后使用随机算法,生成 e5 对应的索引高度 level=2。最后从 level=2 依次向下插入索引对应的有序链表中,如果索引有多层,依次插入 Ln -> Ln-1 -> ...。
- 删除:先将结点对应的 value 设置为 null,标记结点已经被删除。如果查找时有结点 value=null,则说明该结点已经被删除,可以删除该结点。之所以使用标记清除法,是为了将结点和索引的删除操作分开。

每天用心记录一点点。内容也许不重要,但习惯很重要!