Introduction:A Non-Rigorous Review of Deep Learning
原文地址
本篇文章为 MIT 课程 Mathematical Aspects of Deep Learning 的lecture 1 的学习笔记,没有进行完整的翻译,仅供参考
1.深度前向网络(Deep forward networks )
在统计学中,数据以
其中,
我们的目标就是找到一个函数
而深度学习,总的来说就是 parametric statistics的子集。
我们有一个函数族
其中,
我们的目标是找到一个
在这里,
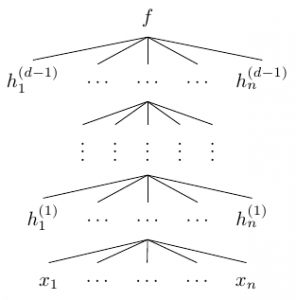
| 图中量 | 含义 | |
|---|---|---|
| 由 |
||
| 网络中的第 |
||
| 第 |
层与层之间宽度不一定相同 | |
| 网络深度 | 第 |
在这里,如果
受神经科学启发:神经细胞会接收多个输入信号,输出两种可能状态。一个最基本的模型设计感知机:
可以描述为
根据这个基本模型,我们可以定义
其中,
那么,
我们希望
或者选择对数函数(logistic function )
或 双曲正切(hyperbolic tangent)
这两个函数与 RELU 相比,优点在于有界性上。
上文中提到过,顶层(top layer)与其它层是不一样的。
顶层通常是scalar-valued
顶层有一些统计上的解释,
h(d−1)1,…,h(d−1)n 被认为是经典统计模型的参数。
顶层的g 要根据这个统计含义来选择。一个例子是线性函数
输出是一个高斯均值。y=WTh+b 另一个例子是函数
σ(wT+b) , 其中σ 是 sigmoid 函数这里认为输出符合伯努利分布,概率x←11+ex P(y) 正比于exp(yz) ,其中z=wT+b - 进一步的,给出 soft-max
softmax(z)i=exp(zi)∑jexp(zj)
其中,z=WTh+b 。这里,z 的组分 就与输出的可能取值相互对应了起来,softmax(z)i 对应的就是取值value 为i 的概率(z 是一个向量,softmax输出为标量,是对矢量z 的每个维度值zi 求了normalized exponential )
Simple example1
> Input : [1, 2, 3, 4, 1, 2, 3],
> Output: [0.024, 0.064, 0.175, 0.475, 0.024, 0.064, 0.175].
>The output has most of its weight where the '4' was in the original input.
>The function highlight the largest values and suppress values which are significantly below the maximum value.例如:向一个网络输入一副图片,输出的
就对应的是这幅图片中是一只猫、狗或青蛙的概率(softmax(z)1,softmax(z)2,softmax(z)3)
在后续几周,我们将关注这些问题:
- 这些函数是怎样近似一般函数的?
- 深度和宽度有怎样的表达能力(expressive power)
- Wikipedia softmax Softmax_function ↩