Floyd 算法应该是最基本,最简单,也是最暴力的最短路算法解法,但是对于一些点数很小的题目,Floyd的表现还是很优秀的,我们先来看一道例题
题目描述给你一个有 (n) ((nleq 100)) 个点以及 (m) ((mleq 800)) 条双向边的图,求出所有点之间的最短路。
输入格式:第一行两个正整数 (n),(m),接下来 (m) 行,每行三个正整数 (u),(v),(w),表示 (u) 和 (v) 之间有一条代价(长度)为 (w) 的边。
输出格式:输出共 (n) 行,每行 (n) 个正整数,第 (i) 行第 (j) 个数,表示点 (i) 到点 (j) 之间的最短路。
样例输入:
5 6
1 3 7
2 4 5
2 3 1
4 3 2
1 5 8
5 2 4
样例输出:
0 8 7 9 8
8 0 1 3 4
7 1 0 2 5
9 3 1 0 7
8 4 5 7 0
对于任何一个操作,我们都可以分成三个部分:1.选择操作容器,2.初始化,3.更新,操作。
比如这一题,让我们求出 所有点 之间的最短路,并以一个 矩阵型 输出,所以我们可以考虑就如题目中的那样,用这个临接矩阵来储存,我们把这个矩阵称为 (operatorname{dis}),用 (operatorname{dis[i][j]}) 来表示 (operatorname{isim j}) 之间的最短路径。
知道了容器,我们就要考虑如何初始化。因为题目让我们求所有点之间的最短路,所以我们可以初始化 (operatorname{dis[i][i]=0}) (可以理解为,我到我自己,相当于没动,所以我不需要耗费任何代价),然后每输入两个点 (u),(v),就将他们输入的代价,作为最初的 (operatorname{dis[u][v]}) 设置为代价 (w),因为在现在看来,这条路是最短的,我们无法从其他地方更新。然后我们考虑一个问题,如果这不是一个 完全图,也就是说,如果并不是每两个点之间都有一条连边,有一些数对(i,j)是没有直接通路的,我们要怎么办?其实非常简单,如果两个点一开始没有直接的连边,我们就可以将它设置成一个不会被重复的值(一般为正无穷或者负无穷,看求的东西),也就是 (operatorname{dis[u][v]=Inf}),于是我们在最开始,就赋值整个数组为正无穷,这样就可以很方便的预处理完成最初的每两个点之间的最短路了。
但是,我们这样并不能直接求出这整个图每两点之间的最短路,因为肯定有一些点没有更新到,并且有一些点之间的最短路点在最后不一定是最短的,这个很好证明,我就不赘述了。于是我们考虑更新,我们拿样例打比方,我们先建出这个图:
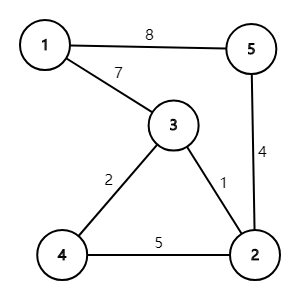
然后按照刚刚的方法初始化一下这个矩阵每个点之间的最初的最短路,大概是这个样子的:
0 ∞ ∞ ∞ ∞ --> 0 ∞ 7 ∞ 8
∞ 0 ∞ ∞ ∞ --> ∞ 0 1 5 4
∞ ∞ 0 ∞ ∞ --> 7 1 0 2 ∞
∞ ∞ ∞ 0 ∞ --> ∞ 5 2 0 ∞
∞ ∞ ∞ ∞ 0 --> 8 4 ∞ ∞ 0
然后就是这个算法最重要的部分了,我们考虑如何更新两个点之间的最短路,来看下面这个简化的图:
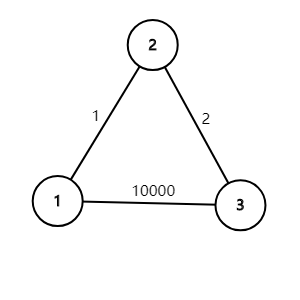
在这个图中,(1sim3) 之间初试化的最短路是 (10000),显然,当我们重新选择 (1sim 2sim3) 这条路的时候,代价就减小到了 (3),比之前那条道路更优秀。这就相当于是在点 (1) 和 (3) 之间,找到一个新的点加入,用 (1sim 2) 与 (2sim3) 来更新这个最短路,可以算作是一种 区间dp 的思想。Floyd 的核心思想就是这个,就是在 两点之间加上一个点 然后和之前的最短路作比较,然后不断更新,达到求出全源最短路的效果。
我们再将这种算法放回原样例中去验证一下,我们从1-n 枚举每个节点 (k) ,用来更新两个点之间是否还有更短的路径。我们从 (1) 开始,我们来看一遍。
用 1 更新:
0 ∞ 7 ∞ 8 --> 0 ∞ 7 ∞ 8
∞ 0 1 5 4 --> ∞ 0 1 5 4
7 1 0 2 ∞ --> 7 1 0 2 ∞
∞ 5 2 0 ∞ --> ∞ 5 2 0 ∞
8 4 ∞ ∞ 0 --> 8 4 ∞ ∞ 0
用 2 更新:
0 ∞ 7 ∞ 8 --> 0 ∞ 7 ∞ 8
∞ 0 1 5 4 --> ∞ 0 1 5 4
7 1 0 2 ∞ --> 7 1 0 2 5
∞ 5 2 0 ∞ --> ∞ 5 2 0 9
8 4 ∞ ∞ 0 --> 8 4 5 9 0
用 3 更新:
0 ∞ 7 ∞ 8 --> 0 8 7 9 8
∞ 0 1 5 4 --> 8 0 1 3 4
7 1 0 2 5 --> 7 1 0 2 5
∞ 5 2 0 9 --> 9 3 2 0 7
8 4 ∞ ∞ 0 --> 8 4 5 7 0
用 4 更新:
0 8 7 9 8 --> 0 8 7 9 8
8 0 1 3 4 --> 8 0 1 3 4
7 1 0 2 5 --> 7 1 0 2 5
9 3 2 0 7 --> 9 3 2 0 7
8 4 5 7 0 --> 8 4 5 7 0
用 5 更新:
0 8 7 9 8 --> 0 8 7 9 8
8 0 1 3 4 --> 8 0 1 3 4
7 1 0 2 5 --> 7 1 0 2 5
9 3 2 0 7 --> 9 3 2 0 7
8 4 5 7 0 --> 8 4 5 7 0
(大家可以配着图来理解)[加粗数字为更新过的最短路]
看起来没什么问题实际也没什么问题,于是我们开是码代码吧。
先是初始化:
memset(dis,0x3f3f3f3f,sizeof(dis));
for(int i=1;i<=n;i++)dis[i][i]=0;
for(int i=1;i<=n;i++)int u,v,w,scanf("%d%d%d",&u,&v,&w),dis[u][v]=w;
第一行就是初始化 (operatorname{dis}) 都为正无穷,0x3f3f3f3f是16进制中的一个数,差不多接近了 INT_MAX 了。
第二行就是自己到自己的最短路
第三行是输入与每两个点之间的最短路初始化。
然后就是 Floyd 啦:
for(int k=1;k<=n;k++)//首先枚举中间加入的点,不然会出错
for(int i=1;i<=n;i++)//然后i,j是枚举每个点,算 i~j 之间的最短路
for(int j=1;j<=n;j++)
dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j]);//Floyd的状态转移方程,这是精华,一定要记牢
这些上面已经讲过了,没懂的可以多看几遍。
看懂了的完整代码应该不难写了,所以整块的代码就不放了。
下面给出几个例题:
- luogu P2888 [USACO07NOV]Cow Hurdles S
- luogu P2935 [USACO09JAN]Best Spot S
- luogu P1522 [USACO2.4]牛的旅行 Cow Tours
当然,Floyd的功能肯定不止求最短路,它还可以做很多的事情,比如下面这道题:
有 (n)((nleq 100)) 个人,他们之间会有 (m) ((mleq 800)) 场比赛,当一个人比了 (n-1) 场比赛后,他就能确定自己的名次,试问共有几个人知道自己的名次?
输入格式:第一行两个正整数 (n),(m)。接下来 (m) 行 每行两行两个 (leq n) 的正整数,表示这两个人之间有一场比赛。
输出格式:一个正整数,表示知道自己名次的人的个数。
样例输入:
5 5
4 3
4 2
3 2
1 2
2 5
样例输出:
2
乍一看没啥思路,但是看到这个数据范围,明显就是放 (n^3) 的算法过吗,而且这个题目还可以抽象成求 有几个点与其他点都相领 的图论问题,所以我们考虑使用 Floyd 算法。
我们按照 Floyd 的方法建图看,将每两条直接连通的边的权值设为 true,不连通就是 (flase)(应该很好理解吧?)。
接下来,我们考虑如何转移状态。按照Floyd的思想,如果两点之间没有直接连边,但是可以通过 加入一个点 来使他们连通,这两个点就是联通的,我们将他抽象成代码。dis[i][j]为true,必须保证 dis[i][j] 本身为true 或者在他们之间加上点 (k),让 dis[i][k] 为true,dis[k][j] 也为true,所以我们得到了以下转移方程:
dis[i][j]=dis[i][j]|(dis[i][k]&dis[k][j]);
| 表示左右两个条件中只要有一个为 真,这个值就为 真。
& 表示左右两个条件中都要为 真,这个值才是 真。
来看下这一题的完整代码:
#include<bits/stdc++.h>
using namespace std;
const int INF=99999999;
const int Inf=0x3f3f3f3f;
const int maxn=305;
const int maxm=25005;
int n,m,t;int dis[maxn][maxn];
int head[maxn],cnt;
int ans;
struct node
{
int nxt,to,w;
}e[maxm];//链式前向星存图,不会的可以直接用dis存。
int times[maxn];
inline void add(int u,int v,int w)
{
e[++cnt].to=v;
e[cnt].nxt=head[u];
e[cnt].w=w;
head[u]=cnt;
}//链式前向星加边操作
inline void get(int u)
{
for(int i=head[u];i;i=e[i].nxt)
{
dis[u][e[i].to]=e[i].w;
}
}//对于每条边的权值,都讲他加入dis里
int main()
{
scanf("%d %d",&n,&m);
for(int i=1;i<=m;i++)
{
int u,v;scanf("%d %d",&u,&v);
add(u,v,1);
}
for(int i=1;i<=n;i++)
{
get(i);
}//预处理dis数组的边权
for(int k=1;k<=n;k++)
{
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
dis[i][j]=dis[i][j]|dis[i][k]&dis[k][j];//状态转移方程&Floyd
}
}
}
for(int i=1;i<=n;i++)
{
int p=1;
for(int j=1;j<=n;j++)
{
if(i==j)continue;
p=p&(dis[i][j]|dis[j][i]);只要这两条边中有一个是联通的,这两点就是联通的
}
ans+=p;
}
printf("%d
",ans);
}
给出题目链接: