题目大意
https://leetcode.com/problems/unique-paths/description/
62. Unique Paths
A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below).
The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked 'Finish' in the diagram below).
How many possible unique paths are there?
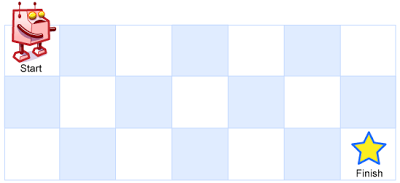
Above is a 7 x 3 grid. How many possible unique paths are there?
Note: m and n will be at most 100.
Example 1:
Input: m = 3, n = 2 Output: 3 Explanation: From the top-left corner, there are a total of 3 ways to reach the bottom-right corner: 1. Right -> Right -> Down 2. Right -> Down -> Right 3. Down -> Right -> Right
Example 2:
Input: m = 7, n = 3
Output: 28
一个机器人位于m x n隔板的左上角(在图中标记为“起点”)。
机器人在任意一点只可以向下或者向右移动一步。机器人尝试到达隔板的右下角(图中标记为“终点”)
有多少种可能的路径?
注意:m和n最多为100
解题思路
思路一:动态规划
状态转移方程:
dp[x][y] = dp[x - 1][y] + dp[x][y - 1]
初始令dp[0][0] = 1
Python代码:
class Solution(object): def uniquePaths(self, m, n): """ :type m: int :type n: int :rtype: int """ dp = [[0] * n for x in range(m)] dp[0][0] = 1 for x in range(m): for y in range(n): if x + 1 < m: dp[x + 1][y] += dp[x][y] if y + 1 < n: dp[x][y + 1] += dp[x][y] return dp[m - 1][n - 1]
上述解法空间复杂度可以优化至O(n):
class Solution(object): def uniquePaths(self, m, n): """ :type m: int :type n: int :rtype: int """ if m < n: m, n = n, m dp = [0] * n dp[0] = 1 for x in range(m): for y in range(n - 1): dp[y + 1] += dp[y] return dp[n - 1]
思路二:排列组合
题目可以转化为下面的问题:
求m - 1个白球,n - 1个黑球的排列方式
公式为:
公式为:C(m + n - 2, n - 1)
Python代码:
class Solution(object): def uniquePaths(self, m, n): """ :type m: int :type n: int :rtype: int """ if m < n: m, n = n, m mul = lambda x, y: reduce(operator.mul, range(x, y), 1) return mul(m, m + n - 1) / mul(1, n)
参考:http://bookshadow.com/weblog/2015/10/11/leetcode-unique-paths/