静态查找:数据集合稳定,不需要添加删除元素的查找操作。
动态查找:查找过程中需要同时添加或删除元素。
查找结构
静态:线性表
动态:二叉排序树、哈希
1. 顺序查找:遍历待查数组,逐个与关键字比较,匹配则查找成功。O(n)
# 设置一个哨兵
def SeqSearch(Array, key):
if Array is None or len(Array) == 0:
return None
i = 0
Array.append(key)
while Array[i] != key:
i += 1
return None if i == len(Array) else i
2. 二分查找
数组必须要有序;数组存在明确的上下界;能够通过索引访问(所以链表就很不适合二分查找)。
# 最普通的情况,规定有序数组不重复
class Solution:
def search(self, nums: List[int], target: int) -> int:
if nums == None or len(nums) == 0:
return -1
low = 0
high = len(nums) - 1
while low <= high: # 双端闭区间[low, high]查找
mid = (low + high) // 2
if nums[mid] == target:
return mid
elif nums[mid] > target:
high = mid - 1
elif nums[mid] < target:
low = mid + 1
return -1
# 寻找左侧边界的二分搜索。初始化 right = nums.length,决定了「搜索区间」是 [left, right),所以决定了 while (left < right),同时也决定了 left = mid + 1 和 right = mid
# 因为需找到 target 的最左侧索引,所以当 nums[mid] == target 时不要立即返回,而要收紧右侧边界以锁定左侧边界。
def search(nums, target):
if nums == None or len(nums) == 0:
return -1
low = 0
high = len(nums)
while low < high: # [low, high) 上搜索
mid = (low + high) // 2
if nums[mid] == target:
high = mid # 找到target之后不要立即返回,缩小搜索区间上界,在[low, mid)中继续搜索,锁定左侧边界low
elif nums[mid] > target:
high = mid
elif nums[mid] < target:
low = mid + 1
if low == len(nums): # target 比所有数都大
return -1
return low if nums[low] == target else -1 # 如果找到,low应该指向左侧边界
# 寻找右侧边界的二分搜索
def search(nums, target):
if nums == None or len(nums) == 0:
return -1
low = 0
high = len(nums)
while low < high: # [low, high) 上搜索
mid = (low + high) // 2
if nums[mid] == target:
low = mid + 1 # 找到target之后不要立即返回,缩小搜索区间下界,在[mid+1, high)中继续搜索,锁定右侧边界high-1
elif nums[mid] > target:
high = mid
elif nums[mid] < target:
low = mid + 1
if low-1 == len(nums): # target 比所有数都大
return -1
return low-1 if nums[low-1] == target else -1 # 若找到,最后low == high,右侧边界在 high-1
# 递归实现二分搜索
class Solution:
def search(self, nums: List[int], target: int) -> int:
if nums == None or len(nums) == 0:
return -1
return self.recursiveSearch(nums, 0, len(nums)-1, target)
def recursiveSearch(self, nums, low, high, target):
if low > high: # 双端闭区间搜索
return -1
mid = (low+high)//2
if nums[mid] == target:
return mid
elif nums[mid] > target:
return self.recursiveSearch(nums, low, mid-1, target)
elif nums[mid] < target:
return self.recursiveSearch(nums, mid+1, high, target)
return -1
3. 插值查找(按比例查找)
数据变化均匀的情况下效率比二分要高。和二分相比唯一的不同在于mid = low + (key - a[low])/(a[high]-a[low])*(high-low)
4. 斐波那契查找(黄金比例查找)
根据斐波那契数列F[k]来放置mid。 F[k] = 1, 1, 2, 3, 5, 8, 13, ...

待查数组元素个数为F[k] - 1
mid = low + F[k-1] -1
def FibonacciSearch(data, key):
F = [0,1]
count = 1;
length = len(data)
low = 0
high = length - 1 # 双端闭区间查找
if(key < data[low] or key > data[high]):
return -1
while F[count] < length: # 生成斐波那契数列
F.append(F[count-1] + F[count])
count = count + 1
low = F[0]
high = F[count] # F[count] 大于或等于length
while len(data)-1 < F[count-1]: # 如果F[count-1]大于数组最大下标,第一次mid=0+F[count-1]就会越界,要将数据个数补全
data.append(data[-1])
while(low <= high): # 双端闭区间
mid = low + F[count-1] # 计算当前分割下标
if(data[mid] > key): # 若查找记录小于当前分割记录
high = mid-1
count = count-1 # 左边数组长度为F[count-1]
elif(data[mid] < key): # 若查找记录大于当前分割记录
low = mid+1
count = count-2 # 右边数组长度为F[count-2]
else: # 若查找记录等于当前分割记录
return mid
return -1
data = [0,1,16,24,35,48,59,62,73,88,99]
key = 35
idx = FibonacciSearch(data, key)
print(data)
print('index for given key:', idx)
5. 线性索引
稠密索引:关键码对目标数据进行一定的提取。索引表对关键码排序形成。只需要对索引表的关键码二分查找即可。应用于数据量不是特别大的时候,因为会导致索引表也非常大。
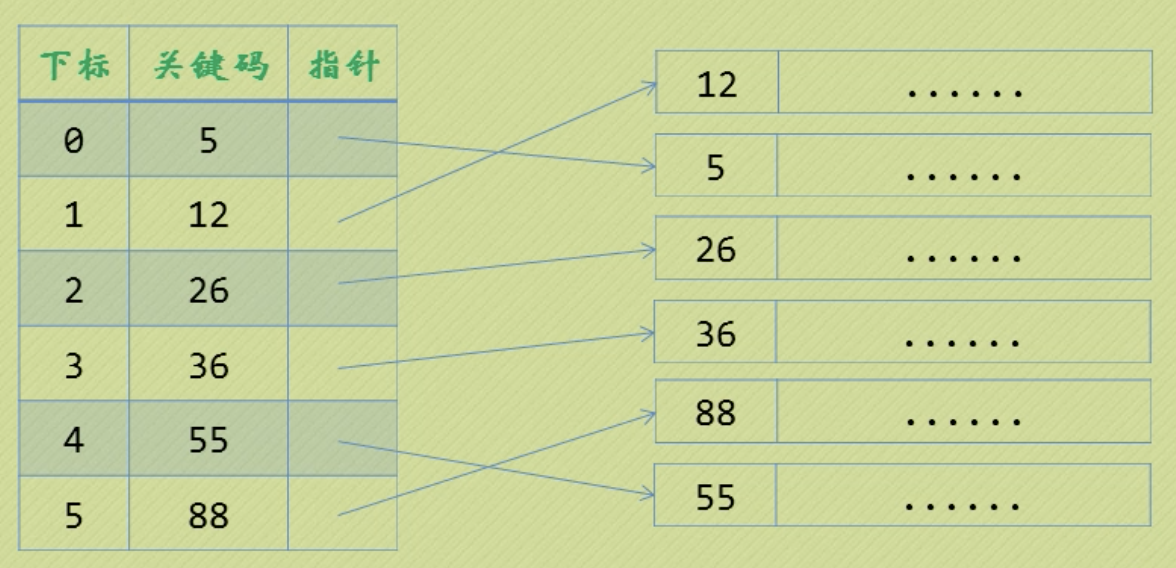
分块索引:不要建立一个数据量等大小的索引表。各个块内部没有排序,各个块之间排序。

倒排索引:反过来由属性来确定记录。

二叉排序树(二叉搜索树)
插入和删除的效率不错,同时查找的效率也很高的算法。
满足:
左子树不为空时,左子树上所有节点的值小于它的根节点的值;
右子树不为空时,右子树上所有节点的值大于它的根节点的值;
左右子树也分别为二叉排序树。
中序遍历二叉排序树,就能得到一个有序序列。二叉树结构有利于插入删除操作。
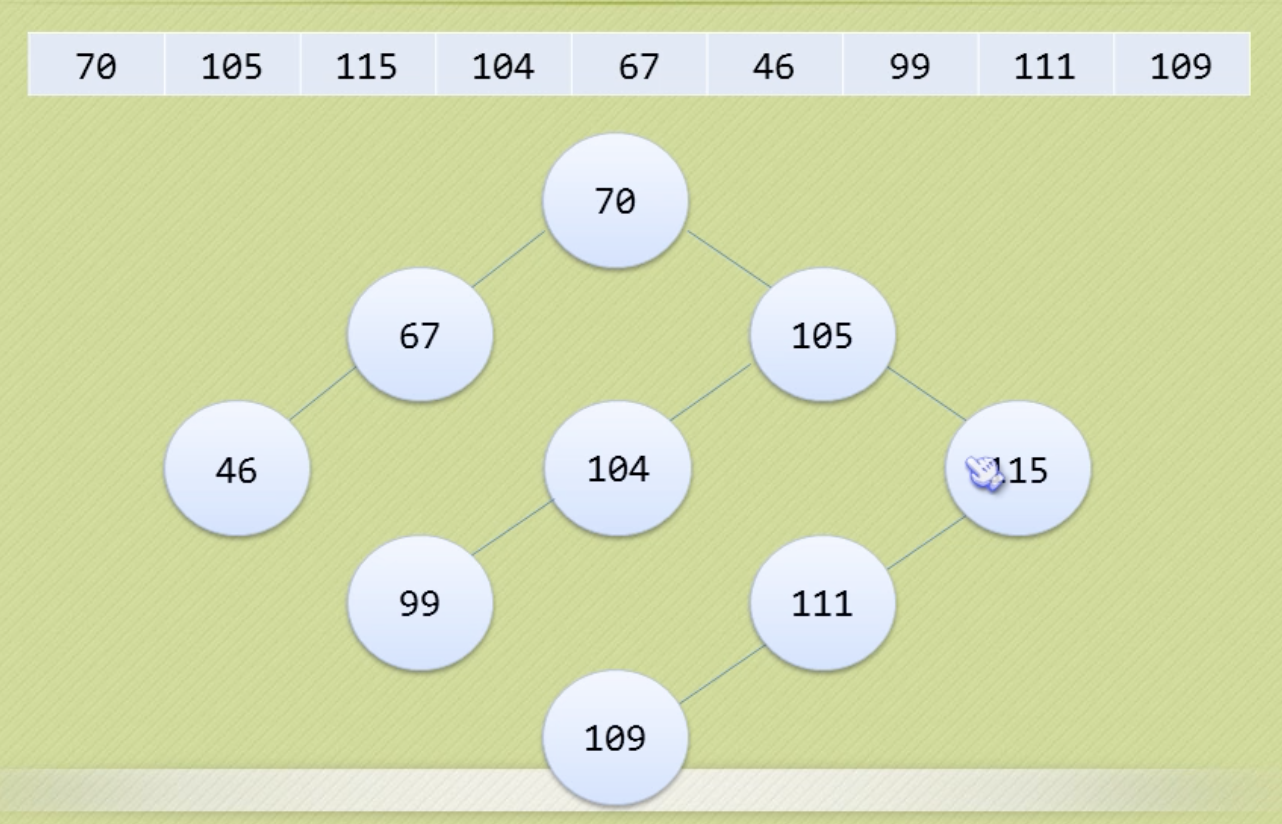
查找、插入、删除
class Node:
def __init__(self, data):
self.data = data
self.lchild = None
self.rchild = None
class BST:
def __init__(self, node_list):
self.root = Node(node_list[0])
for data in node_list[1:]:
self.insert(data) # 插入元素创建二叉排序树
# 搜索
def search(self, node, parent, key): # 开始搜索的节点node,其父节点parent,关键字key
if node is None:
return False, node, parent
if node.data == key:
return True, node, parent # 如果当前节点的val等于key,返回搜索结果
if node.data > key:
return self.search(node.lchild, node, data) # 如果当前节点的val大于key,去左子树搜索
else:
return self.search(node.rchild, node, data) # 如果当前节点的val大于key,去右子树搜索
# 插入
def insert(self, data):
flag, n, p = self.search(self.root, self.root, data)
if not flag: # 如果二叉排序中不存在待插入节点,找到新节点的父节点
new_node = Node(data) # 创建新节点
if data > p.data: # 判断新节点是父节点的左孩子还是右孩子,然后插入即可
p.rchild = new_node
else:
p.lchild = new_node
# 删除
def delete(self, root, data):
flag, n, p = self.search(root, root, data)
if flag is False:
print("无该关键字,删除失败")
else:
if n.lchild is None: # 若待删节点n的左子树为空
if n == p.lchild: # 若n是其父节点p的左子树,则n的右子树变为p的左子树
p.lchild = n.rchild
else:
p.rchild = n.rchild # 若n是p的右子树,则n的右子树变为p的右子树
elif n.rchild is None: # 若n的右子树为空
if n == p.lchild:
p.lchild = n.lchild
else:
p.rchild = n.lchild
else: # 若n的左右子树均不为空
pre = n.rchild
if pre.lchild is None: # 若n的右子树的左子树为空
n.data = pre.data # n右子树的数据赋给n
n.rchild = pre.rchild # n的右子树变为n的右子树的右子树
else: # 若n的右子树的左子树不为空
next = pre.lchild
while next.lchild is not None: # 一直向左遍历到左子树为空的节点
pre = next
next = next.lchild
n.data = next.data # 把左子树为空的节点的数据赋给n
pre.lchild = next.rchild # 该节点的右子树链到该节点的父节点的左子树
# 先序遍历
def preOrderTraverse(self, node):
if node is not None:
print(node.data)
self.preOrderTraverse(node.lchild)
self.preOrderTraverse(node.rchild)
# 中序遍历
def inOrderTraverse(self, node):
if node is not None:
self.inOrderTraverse(node.lchild)
print(node.data)
self.inOrderTraverse(node.rchild)
# 后序遍历
def postOrderTraverse(self, node):
if node is not None:
self.postOrderTraverse(node.lchild)
self.postOrderTraverse(node.rchild)
print(node.data)
a = [49, 38, 65, 97, 60, 76, 13, 27, 5, 1]
bst = BST(a) # 创建二叉查找树
print('遍历')
bst.inOrderTraverse(bst.root) # 中序遍历
print('删除元素')
bst.delete(bst.root, 49)
bst.inOrderTraverse(bst.root)
print('搜索')
res, node, parent = bst.search(bst.root, None, 97)
print(res, node.data, parent.data)
平衡二叉排序树 AVL
避免以下二叉排序树的情况,防止二叉排序树退化成链。
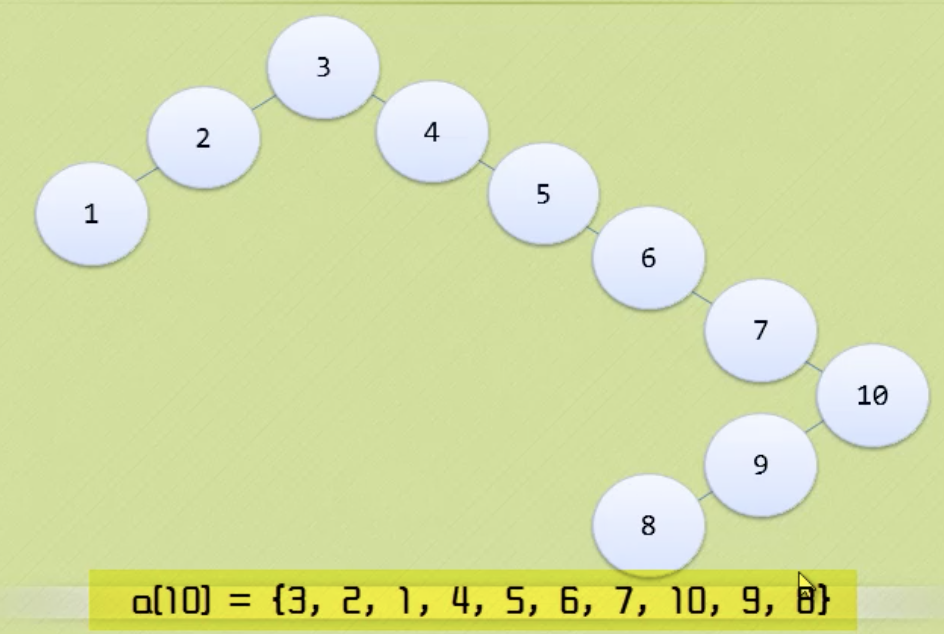
平衡二叉排序树:要么是一颗空树,要么是一颗二叉排序树,且左右子树深度之差的绝对值不超过1,且左右子树都是平衡二叉排序树。
构建方法:在构建二叉排序树时,每插入一个节点,就检查树的平衡性是否被破坏(平衡因子大于1,左子树深度-右子树深度)。 如果被破坏,就旋转最小不平衡子树。遍历与查找和普通二叉排序树一样,但插入和删除需要考虑平衡性问题。
平衡被破坏的四种情况:
- 插入点位于X的左子节点的左子树——左左
- 插入点位于X的左子节点的右子树——左右
- 插入点位于X的右子节点的左子树——右左
- 插入点位于X的右子节点的右子树——右右
对于上面四中情况,可以分为两类:

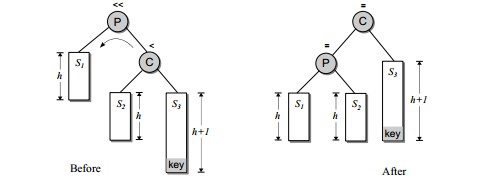
1、外侧插入:左左、右右,都是又往边上发展了。
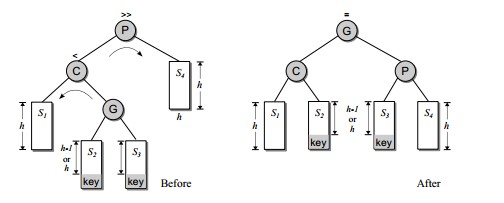
2、内侧插入:左右、右左,都是往里面来了些。
恢复平衡的方法:外侧插入单旋转、内侧插入双旋转。
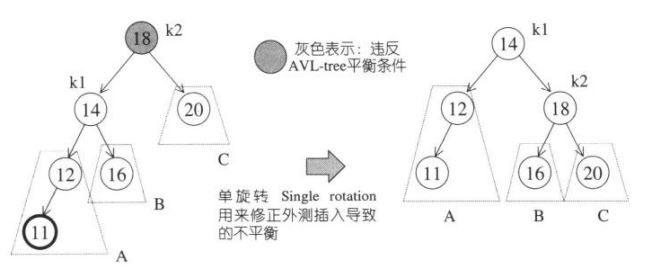
先看图中外侧插入11,使得k2点平衡因子为3-1=2>1,为了恢复平衡,想象把k1点提起,k2自然下滑,把k1的右子树B挂到k2的左侧。
为什么这么做了:
1. 根据二叉排序树的性质,k2 > k1,所以k2必须成为新树形中的k1节点的右子节点。(k1向上提起,使k2自然下滑)
2. 同样根据性质,B子树的所有节点的键值都在k1和k2之间,也就是大于k1,小于k2,那就是在k1的右子树上,k2的左子树上,因此将B子树挂到k2的左侧(将B子树挂到k2的左侧)。最终调整后的图如上右图,这是左左,右右的情况一样。
注意调整后k1和k2的深度

def LL_Rotate(self, node):
k1 = node.left # 不平衡点的左子树k1
node.left = k1.right # k1的右子树的所有值都介于kl和node的值之间,所以将其设置为node的左子树
k1.right = node # 提起n点,node自然下滑。即node变为n的右子树
node.height = max(self.height(node.left), self.height(node.right)) + 1
k1.height = max(self.height(k1.left), self.height(node)) + 1
return k1
def RR_Rotate(self, node):
k1 = node.right
node.right = k1.left
k1.left = node
node.height = max(self.height(node.right), self.height(node.left)) + 1
k1.height = max(self.height(k1.right), self.height(node)) + 1
return k1
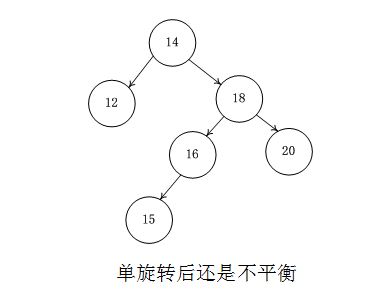
再看内侧插入的情况,图中插入15后k3点不平衡,k1上提k3自然落下k1右子树挂到k3左端,这样单旋转后发现还是不平衡的。

所以就需要先对k1、k2进行单旋转,然后再对k2、k3单旋转。即先对k1做RR_rotate,再对k3做LL_rotate
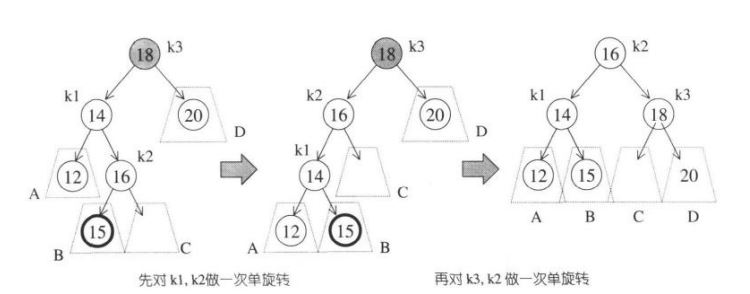
def LR_rotate(self, node):
node.left = self.RR_rotate(node.left)
return self.LL_rotate(node)
右左的情况类似

def RL_rotate(self, node):
node.right = self.LL_rotate(node.right)
return self.RR_rotate(node)
插入:
def height(self, node):
if node is None:
return -1
return node.height
def insert(self, key):
self.root = self._insert(key, self.root)
def _insert(self, key, node):
if node is None: # 要插入的树空
node = Node(key)
return node
if key == node.data: # 要插入的树中存在重复元素
print('重复元素,插入失败')
return node
if key < node.data: # 要插入的值小于根节点
node.left = self._insert(key, node.left) # 插入左子树中
# 判断平衡性
if self.height(node.left) - self.height(node.right) > 1:
if key < node.left.data: # 插入节点位于node左孩子的左子树中
node = self.LL_rotate(node) # 左左单旋转
else:
node = self.LR_rotate(node) # 插入的节点位于node左孩子的右子树中,左右双旋转
elif key > node.data: # 插入值大于根节点
node.right = self._insert(key, node.right) # 插入右子树中
if self.height(node.right) - self.height(node.left) > 1:
if key > node.right.data:
node = self.RR_rotate(node)
else:
node = self.RL_rotate(node)
node.height = max(self.height(node.left), self.height(node.right) + 1
return node
删除:
1.当前节点为要删除的节点且是叶子(无子树),直接删除,当前节点(为None)的平衡不受影响。
2.当前节点为要删除的节点且只有一个左儿子或右儿子,用左儿子或右儿子代替当前节点,当前节点的平衡不受影响。
3.当前节点为要删除的节点且有左子树右子树:如果右子树高度较高,则从右子树选取最小节点,将其值赋予当前节点,然后删除右子树的最小节点。如果左子树高度较高,则从左子树选取最大节点,将其值赋予当前节点,然后删除左子树的最大节点。这样操作当前节点的平衡不会被破坏。
4.当前节点不是要删除的节点,则对其左子树或者右子树进行递归操作。当前节点的平衡条件可能会被破坏,需要进行平衡操作。
def search(self, node, key):
if node is None:
return False, node
if node.data == key:
return True, node
if node.data > key:
return self.search(node.lchild, key)
else:
return self.search(node.rchild, key)
def findMin(self, node):
if node.left: # 如果存在左子树,就一直去左子树里找最小
return self.findMin(node.left)
return node # 没有左子树的话,当前根就是最小
def findMax(self, node):
if node.right: # 如果存在右子树,就去右子树找最大
return self.findMax(node.right)
return node # 没有右子树的话,当前根就是最大
def delete(self, key):
self.root = self.remove(key, self.root)
def remove(self, key, node):
if node is None: # node是None,两种情况:上来就是空树;递归到最后没有找到待删元素
print("没找到关键字,删除失败")
return node
if key == node.data: # 要删除的就是当前的根节点
if node.left and node.right: # 左右子树都不空
if self.height(node.left) > self.height(node.right): # 在高度更大的子树上进行操作
# 左子树高度大,删除左子树中元素最大的的节点,同时将其值赋给当前根节点
# 这样新的根节点值还是能保证比其左子树任意节点都大,node的平衡性不会被破坏
maxNode = self.findMax(node.left)
node.data = maxNode.data # 因为当前根节点一定比其左子树任意节点都大
node.left = self.remove(node.data, node.left) # 去node的左子树把原来最大的元素节点删除
else:
# 右子树高度大
minNode = self.findMin(node.right)
node.data = minNode.data
node.right = self.remove(node.data, node.right)
node.height = max(self.height(node.left), self.height(node.right)) + 1
else: # 左右子树中有一个为空,或者全为空
if node.right:
node = node.right # 左空右不空,直接用右子树代替node
elif node.left:
node = node.left # 右空左不空,左子树代替node
node.height = max(self.height(node.left), self.height(node.right)) + 1
else:
node = None # 都空,直接用None(也即左子树)代替node
elif key < node.data: # 要删除的不是当前子树的根节点,去其左子树或右子树递归删除,当前节点平衡性可能被破坏
node.left = self.remove(key, node.left) # 去node左子树删除,可能导致左低右高
if self.height(node.right) - self.hight(node.left) > 1: # 当前节点node不平衡,左低右高
if self.height(node.right.left) > self.height(node.right.right): # node右子树的左子树更高,双旋转
node = self.RL_rotate(node)
else: # node右子树的右子树更高,右右单旋转
node = self.RR_rotate(node)
node.height = max(self.height(node.left), self.height(node.right)) + 1
else: # key > node.data,去node的右子树递归删除
node.right = self.remove(key, node.right)
if self.height(node.left) - self.height(node.right) > 1: # node失去平衡,左高右低
if self.height(node.left.right) > self.height(node.left.left): # node左子树的右子树更高,双旋转
node = self.LR_rotate(node)
else:
node = self.LL_rotate(node) # 左左单旋转
node.height = max(self.height(node.left), self.height(node.right)) + 1
return node
多路查找树
降低对外部存储结构的访问次数。每一个节点的孩子可以多于两个,每个节点可以存储多个元素。
2-3树,每一个节点都具有两个孩子或三个孩子。左子树元素小于节点元素小于右子树元素。但不同于二叉排序树的是,2节点要么没孩子要么有两个孩子,不能只有一个孩子。3节点要么没孩子要么有三个孩子,且从左到右变大。2-3树所有叶子都要在同一层次上。
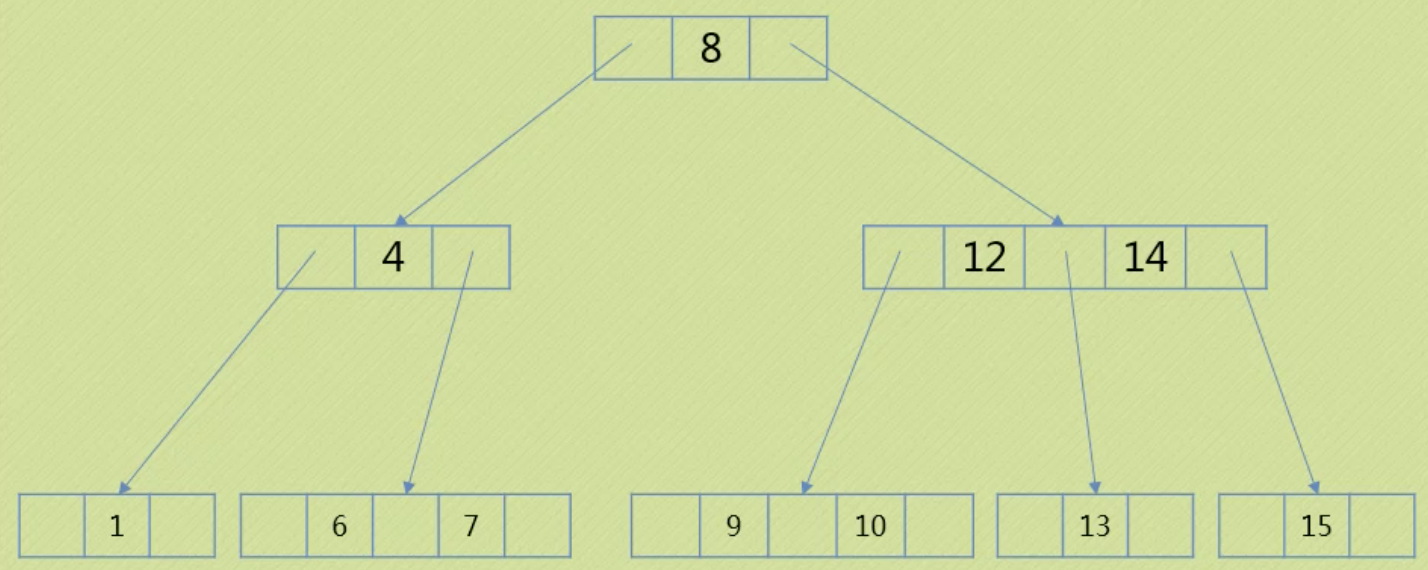
2-3树的插入:
1. 空树,建立一个2节点作为根节点即可。
2.插入进一个2节点,例如上图中插入3,把2节点变为3节点插入即可。

3.插入进一个3节点,三种情况。第一种,插入的叶子是3节点,上面的父节点是2节点,通过扩展父节点。例如上图中插入5,不能再从6向下扩展,则拆分3节点后向上扩展,把父节点扩展为3节点,再调整位置。

第二种情况,插入的叶子是3节点,父节点也是3节点,一直向上找父节点为2节点为止,扩展2节点。例如插入11,第三层的3节点满了,向上一层的3节点也满了,再向上找到2节点进行扩展,调整后还是要保持中序遍历结果是有序的。

第三种情况,如果一直向上找到根节点都是3节点,就需要增加高度来插入。例如再插入2,增加层以后,上面的3节点都需要拆成2节点来保证叶子都在同一层。

2-3树的删除:
1. 要删除的元素在一个3节点叶子上。直接删除即可,不会影响树结构。

2. 所删除的元素位于2节点的叶子上

分四种情况:此节点双亲也是2节点,且拥有一个3节点的右孩子,直接删除不行,拆分3节点后左旋转

此节点的双亲是2节点,且拥有一个2节点的右孩子,再拆一个3节点才行。注意根节点的左子树的最右节点元素是根节点元素直接前驱,根节点右子树的最左节点元素是根节点元素直接后继,所以补位后左旋转:

此节点的双亲是3节点。把双亲变2节点即可:
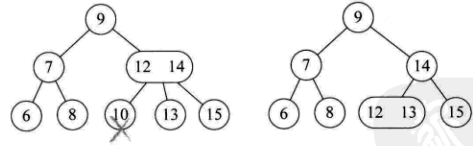
当前树是一个满二叉树,降低树高:

3. 所删元素位于非叶子的分支节点。此时按树中序遍历得到此元素的前驱或后续元素,补位:
分支节点是2节点

分支节点是3节点

2-3-4树,基于2-3树的扩展,多了一种4节点的情况。要么没有孩子,要么有4个孩子。其他性质和2-3树一致。
2-3-4树的插入:
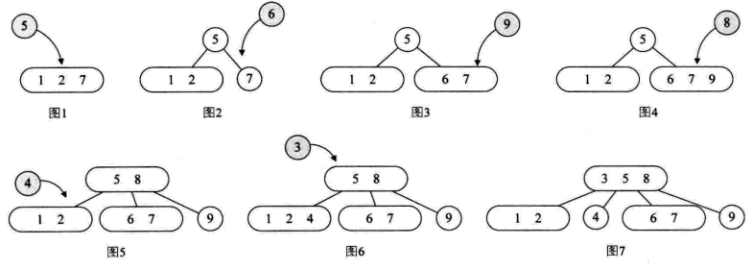
2-3-4树的删除:

B树
2-3树是3阶B树,2-3-4树是4阶B树。

哈希表查找
不通过比较,直接得到关键字的位置。记录的存储位置 = f(关键字),每个关键字key对应一个存储位置f(key)。存储和查找的时候使用的哈希函数相同即可。但可能出现一个哈希地址对应多个记录的情况,即哈希冲突。在设计哈希函数时要令哈希冲突尽可能少。