Given an m x n matrix of positive integers representing the height of each unit cell in a 2D elevation map, compute the volume of water it is able to trap after raining.
Note:
Both m and n are less than 110. The height of each unit cell is greater than 0 and is less than 20,000.
Example:
Given the following 3x6 height map: [ [1,4,3,1,3,2], [3,2,1,3,2,4], [2,3,3,2,3,1] ] Return 4.
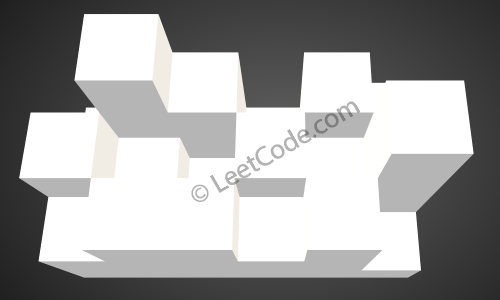
The above image represents the elevation map [[1,4,3,1,3,2],[3,2,1,3,2,4],[2,3,3,2,3,1]] before the rain.
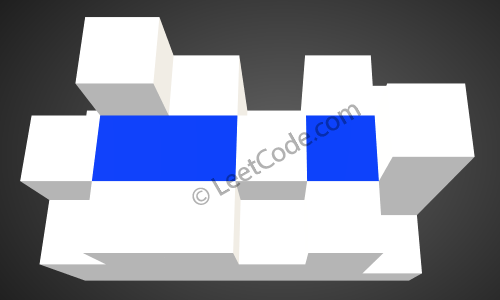
After the rain, water are trapped between the blocks. The total volume of water trapped is 4.
此题是Trapping Rain Water的变体,开始并没有想出来,看了大神的答案才恍然大悟。首先先思考再trapping rain water是怎么做的,我们用two pointer从外向里遍历,而此题方法与那道题目类似,是从外向里遍历,那么如何把边界包括进去呢?这里面需要用到小顶堆的用法了,首先定义一个cell类,存放row,col和height;再定义一个visited二维数组,用来确定是否访问过该cell;然后把边界的这些cell存放到小顶堆里面,因为小顶堆有自动按照从小到达将height排序的功能,先取出来的是较小height的cell,然后检测cell四周没有访问过的且不超过边界值的cell高度,如果未访问过的cell高度小于边界的高度,则高度差为该点存水的容积,否则不存水,全部遍历就是所要结果了,代码如下:
public class Solution {
public class Cell{
int row;
int col;
int height;
public Cell(int row,int col,int height){
this.row = row;
this.col = col;
this.height = height;
}
}
public int trapRainWater(int[][] heightMap) {
if(heightMap==null||heightMap.length==0||heightMap[0].length==0) return 0;
int m = heightMap.length;
int n = heightMap[0].length;
boolean[][] visited =new boolean[m][n];
int sum = 0;
PriorityQueue<Cell> pq = new PriorityQueue<>(1,new Comparator<Cell>(){
public int compare(Cell a,Cell b){
return a.height-b.height;
}
});
for(int i=0;i<m;i++){
visited[i][0] = true;
visited[i][n-1] = true;
pq.offer(new Cell(i,0,heightMap[i][0]));
pq.offer(new Cell(i,n-1,heightMap[i][n-1]));
}
for(int i=0;i<n;i++){
visited[0][i]= true;
visited[m-1][i] = true;
pq.offer(new Cell(0,i,heightMap[0][i]));
pq.offer(new Cell(m-1,i,heightMap[m-1][i]));
}
int[][] dirs = new int[][]{{0,1},{0,-1},{-1,0},{1,0}};
while(!pq.isEmpty()){
Cell cell = pq.poll();
for(int[] dir:dirs){
int row = cell.row+dir[0];
int col = cell.col+dir[1];
if(row>=0&&row<m&&col>=0&&col<n&&!visited[row][col]){
visited[row][col] = true;
sum+=Math.max(0,cell.height-heightMap[row][col]);
pq.offer(new Cell(row,col,Math.max(cell.height,heightMap[row][col])));
}
}
}
return sum;
}
}