2012 #5 Gold miner

Gold miner

Time Limit: 4000/2000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 1889    Accepted Submission(s): 740
Time Limit:2000MS     Memory Limit:32768KB     64bit IO Format:%I64d & %I64u

Submit Status Practice HDU 4341

Problem Description

Homelesser likes playing Gold miners in class. He has to pay much attention to the teacher to avoid being noticed. So he always lose the game. After losing many times, he wants your help.

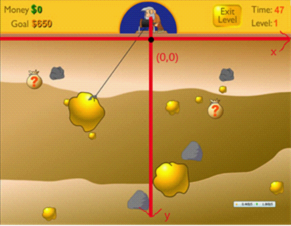
To make it easy, the gold becomes a point (with the area of 0). You are given each gold's position, the time spent to get this gold, and the value of this gold. Maybe some pieces of gold are co-line, you can only get these pieces in order. You can assume it can turn to any direction immediately.
Please help Homelesser get the maximum value.

 

Input

There are multiple cases.
In each case, the first line contains two integers N (the number of pieces of gold), T (the total time). (0＜N≤200, 0≤T≤40000)
In each of the next N lines, there four integers x, y (the position of the gold), t (the time to get this gold), v (the value of this gold). (0≤|x|≤200, 0＜y≤200,0＜t≤200, 0≤v≤200)

 

Output

Print the case number and the maximum value for each test case.

 

Sample Input

3 10 1 1 1 1 2 2 2 2 1 3 15 9 3 10 1 1 13 1 2 2 2 2 1 3 4 7

 

Sample Output

Case 1: 3 Case 2: 7

 

Author

HIT

 

Source

2012 Multi-University Training Contest 5

 

Recommend

zhuyuanchen520

#include <stdio.h>
#include <string.h>
#include <cmath>
#include <algorithm>
using namespace std;

struct Node 
{
    int x;
    int y;
    int t;
    int v;
}a[205];

bool cmp(Node pp,Node qq)
{
    double px,py,qx,qy;
    px=(double)pp.x,py=(double)pp.y;
    qx=(double)qq.x,qy=(double)qq.y;
    if(fabs(atan2(px,py)-atan2(qx,qy))>(1e-8))
    {
        return atan2(px,py)<atan2(qx,qy);
    }
    else
    {
        return (px*px+py*py)<(qx*qx+qy*qy);
    }
}

bool compare(Node pp,Node qq)
{
    double px,py,qx,qy;
    px=(double)pp.x,py=(double)pp.y;
    qx=(double)qq.x,qy=(double)qq.y;
    if(fabs(atan2(px,py)-atan2(qx,qy))<=(1e-8))
        return true;
    else
        return false;
}

int dp[205][40005],coc[205][40005];

int main()
{
    int n,T,cas=1;
    int i,j,k;
    int b[205];
    while(scanf("%d %d",&n,&T)!=EOF)
    {
        memset(b,0,sizeof(b));    
        for(i=1;i<=n;i++)
            scanf("%d %d %d %d",&a[i].x,&a[i].y,&a[i].t,&a[i].v);
        sort(a+1,a+n+1,cmp);
        for(i=1;i<n;i++)
        {
            for(j=i+1;j<=n;j++)
            {
                if(compare(a[i],a[j]))
                    b[i]++;
                else
                    break;
            }
        }
        for(i=0;i<=n;i++)
        {
            for(j=0;j<=T;j++)
            {
                dp[i][j]=0;
                coc[i][j]=0;
            }
        }

        for(i=1;i<=n;i++)
        {
            for(j=0;j<=T;j++)
            {
                dp[i][j]=coc[i][j];
            }

            for(j=0;j+a[i].t<=T;j++)
            {
                dp[i][j+a[i].t]=max(dp[i][j+a[i].t],coc[i][j]+a[i].v);
                if(b[i]>0)
                {
                    coc[i+1][j+a[i].t]=max(coc[i+1][j+a[i].t],coc[i][j]+a[i].v);
                }
            }

            for(j=0;j<=T;j++)
            {
                dp[i][j]=max(dp[i-1][j],dp[i][j]);
                coc[i+b[i]+1][j]=max(coc[i+b[i]+1][j],dp[i][j]);
            }
        }

        /*for(i=1;i<=n;i++)
            printf("%d ",a[i].v);
        printf("

");
        for(i=1;i<=n;i++)
        {
            for(j=1;j<=T;j++)
            {
                printf("%d ",coc[i][j]);
            }
            printf("
");
        }
        printf("
");
        for(i=1;i<=n;i++)
        {
            for(j=1;j<=T;j++)
            {
                printf("%d ",dp[i][j]);
            }
            printf("
");
        }
        printf("
");*/

        int ans=0;
            for(j=0;j<=T;j++)
                if(dp[n][j]>ans)
                    ans=dp[n][j];
        printf("Case %d: %d
",cas++,ans);
    }
    return 0;
}