【线段树】【HDU1754】I Hate It(区间最大值，单点更新)

链接：http://acm.hdu.edu.cn/showproblem.php?pid=1754

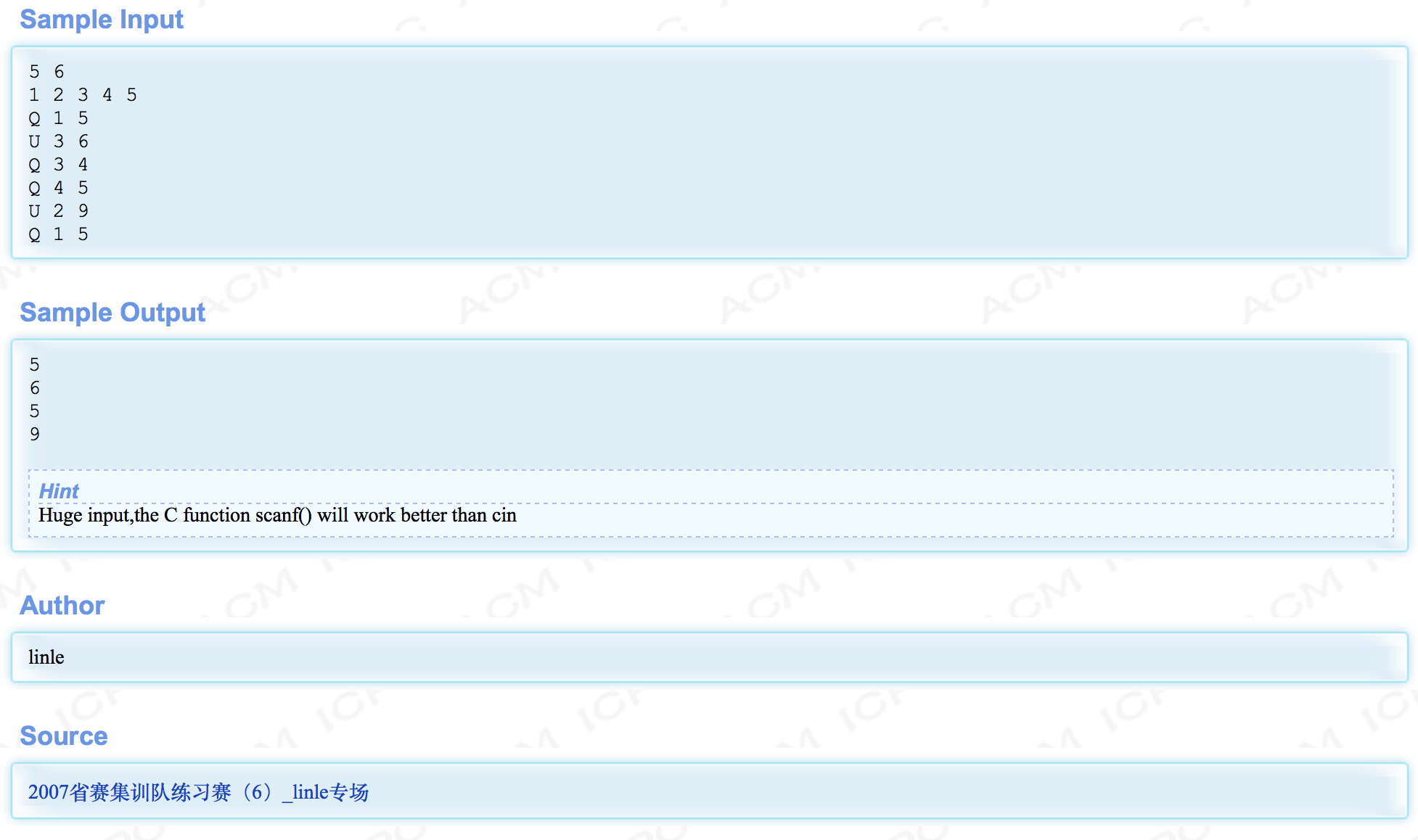
单点更新，求区间最大值

// https://blog.csdn.net/panyanyany/article/details/6776300
#define _CRT_SBCURE_NO_DEPRECATE
#include <cmath>
#include <string>
#include <cstdio>
#include <cstdlib>
#include <iostream>
using namespace std;

const int N = 200010;

int num[N];
struct node
{
    int l,r;
    int mmax;   // 此题只有询问最高成绩的操作，因此不需要存储区间和
    int mid()
    {
        return (l+r)/2;
    }
}tree[N*4];

// 构建线段树
int BuildTree(int root,int l,int r)
{
    // 当前节点所表示的区间
    tree[root].l = l;
    tree[root].r = r;
    // 若左右区间相同，则此节点为叶子节点，mmax赢储存对应某个学生的值
    if(l == r)
    {
        return tree[root].mmax = num[l];
    }
    // 递归建立左右子树，并从子书中获得最大值
    int a,b;
    a = BuildTree(root*2,l,(l+r)/2);
    b = BuildTree(root*2+1,(l+r)/2+1,r);

    return tree[root].mmax = max(a,b);
}

// void add(int root,int i,int t)
// {
//     // tree[root].sum += t;
//     if(tree[root].l == i && tree[root].r == i)
//         return ;
//     if(i <= tree[root].mid())
//         add(root*2,i,t);
//     else
//         add(root*2+1,i,t);
// }




// 从节点root开始，查找l和r之间的最大值
int find(int root,int l,int r)
{
    // 若此区间与root所管理的区间无交集
    if(tree[root].l > r || tree[root].r < l)
        return 0;
    // 若此区间包含root所管理的区间
    if(l <= tree[root].l && tree[root].r <= r)
        return tree[root].mmax;
    // 递归搜索左右子树，取最大值
    int a,b;
    a = find(root*2,l,r);
    b = find(root*2+1,l,r);
    return max(a,b);
}
// 更新pos点的值
int update(int root,int pos,int val)
{
    // 若pos不存在于root所管理的区间内
    if(pos < tree[root].l || tree[root].r < pos)
        return tree[root].mmax;

    // 若root正好是一个符合条件的叶子
    if(tree[root].l == pos && tree[root].r == pos)
        return tree[root].mmax = val;
    
    // 否则···
    int a,b;
    a = update(root*2,pos,val);
    b = update(root*2+1,pos,val);

    // 更新最大值
    tree[root].mmax = max(a,b);

    return tree[root].mmax;
}


// int query(int root,int s,int e)
// {
//     if(tree[root].l == s && tree[root].r == e)
//         return tree[root].mmax;
//     if(e <= tree[root].mid())
//         return query(root*2,s,e);
//     else
//         if(s > tree[root].mid())
//             return query(root*2+1,s,e);
//         else
//             return max(query(root*2,s,tree[root].mid()),query(root*2+1,tree[root].mid()+1,e));
// }

int main()
{
    int n,m,i,a,b;
    char s;
    while(scanf("%d %d",&n,&m)!=EOF)
    {
        for(i = 1;i <= n;i++)
            scanf("%d",&num[i]);
        BuildTree(1,1,n);
        for(i = 1;i <= m;i++)
        {
            getchar();
            scanf("%c",&s);
            if(s == 'Q')
            {
                scanf("%d %d",&a,&b);
                printf("%d
",find(1,a,b));
            }
            if(s == 'U')
            {
                scanf("%d %d",&a,&b);
                update(1,a,b);
            }
    }
    }
    return 0;
}