The RL problem

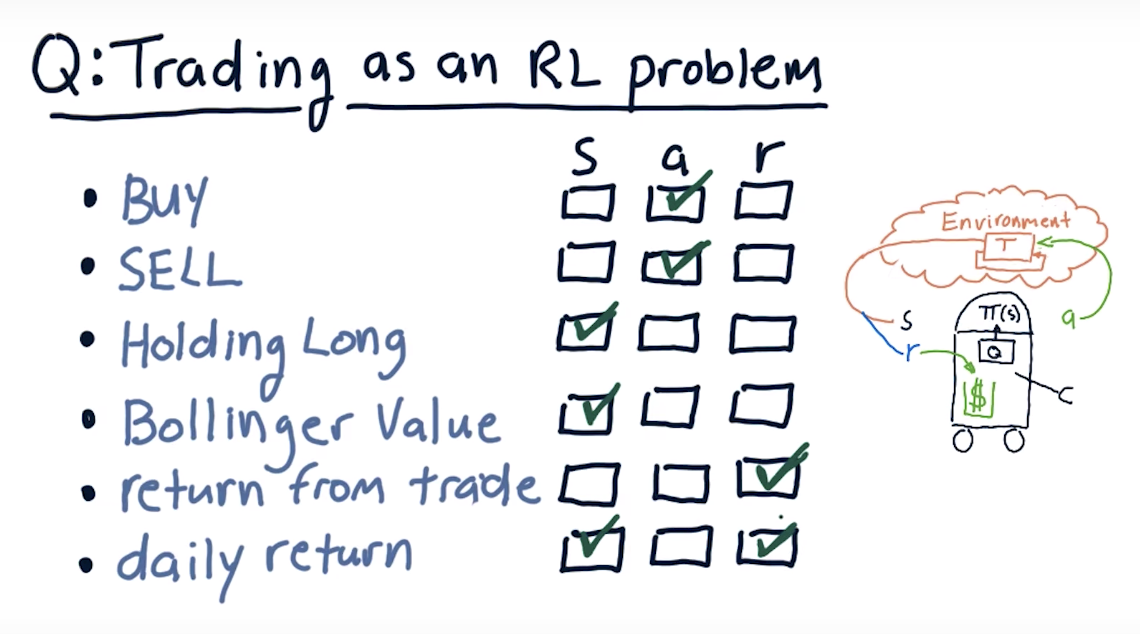
Trading as an RL problem
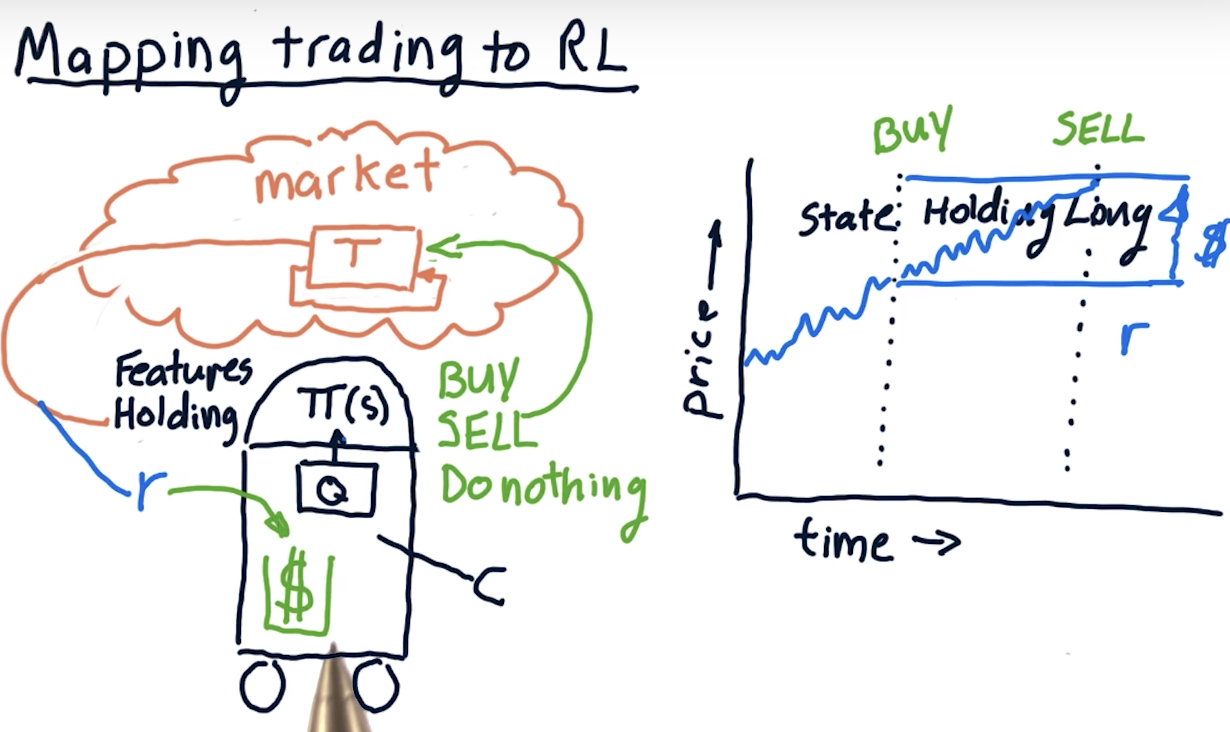
Mapping trading to RL
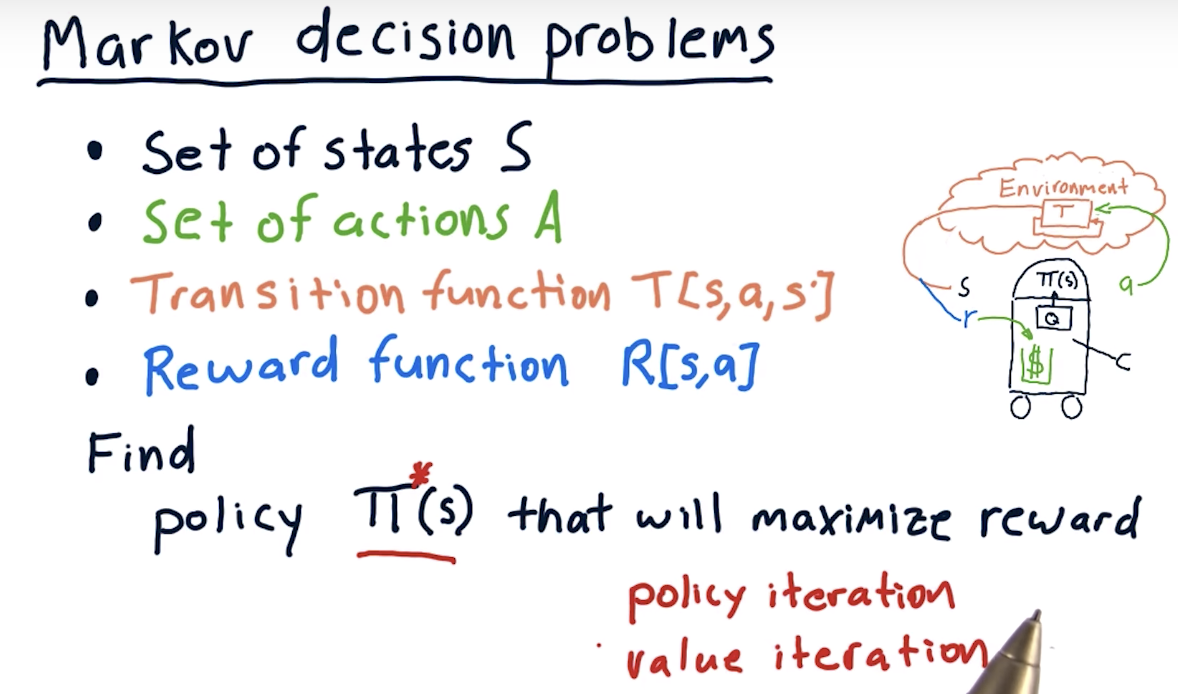
Markov decision problems
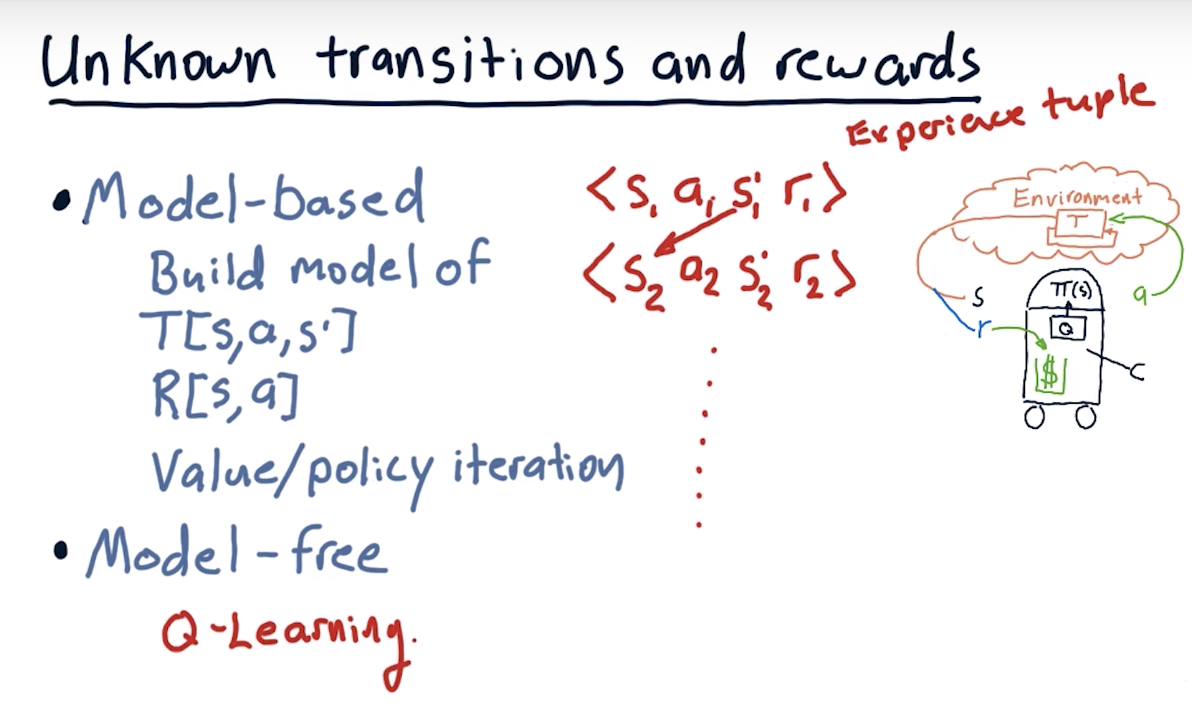
Unknown transitions and rewards
What to optimize?




Learning Procedure

Update Rule
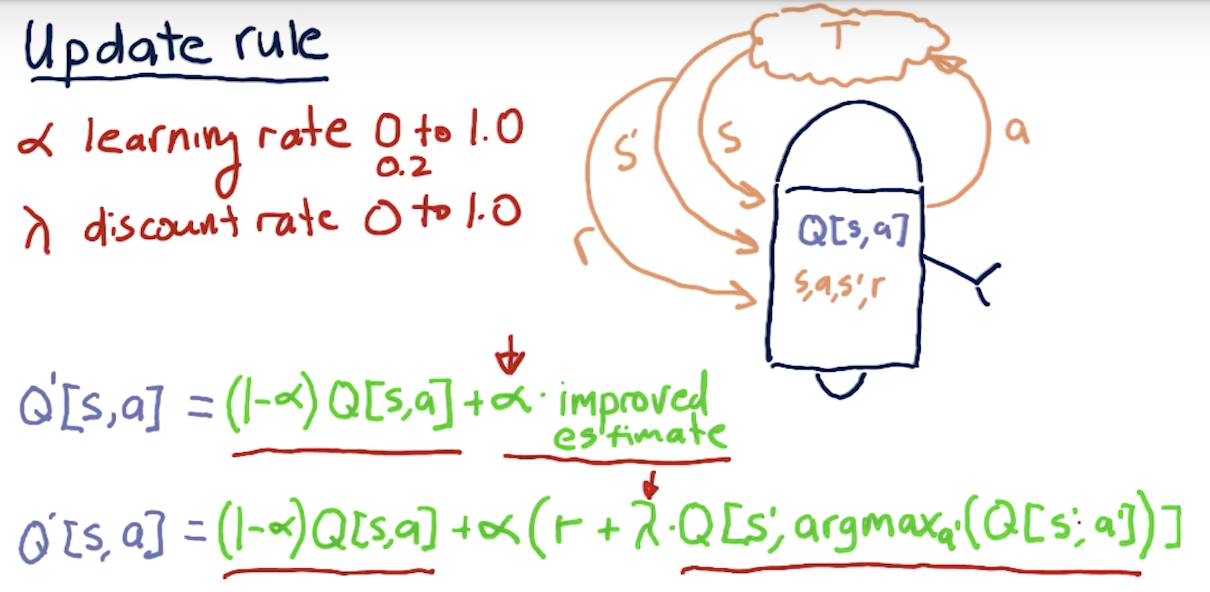
Update Rule
The formula for computing Q for any state-action pair <s, a>, given an experience tuple <s, a, s', r>, is:Q'[s, a] = (1 - α) · Q[s, a] + α · (r + γ · Q[s', argmaxa'(Q[s', a'])])
Here:
r = R[s, a]is the immediate reward for taking actionain states,γ ∈ [0, 1](gamma) is the discount factor used to progressively reduce the value of future rewards,s'is the resulting next state,argmaxa'(Q[s', a'])is the action that maximizes the Q-value among all possible actionsa'froms', and,α ∈ [0, 1](alpha) is the learning rate used to vary the weight given to new experiences compared with past Q-values.
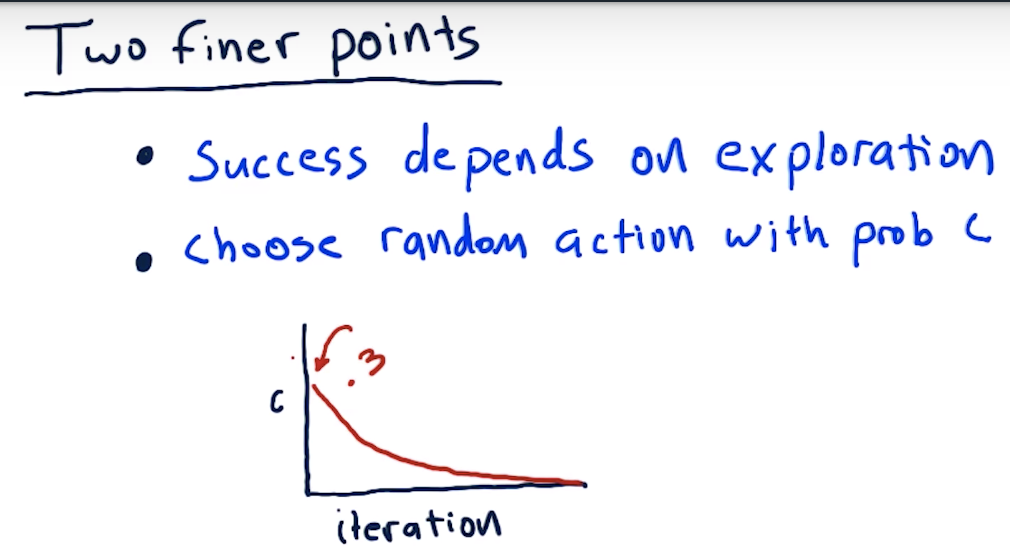
Two Finer Points
The Trading Problem: Actions
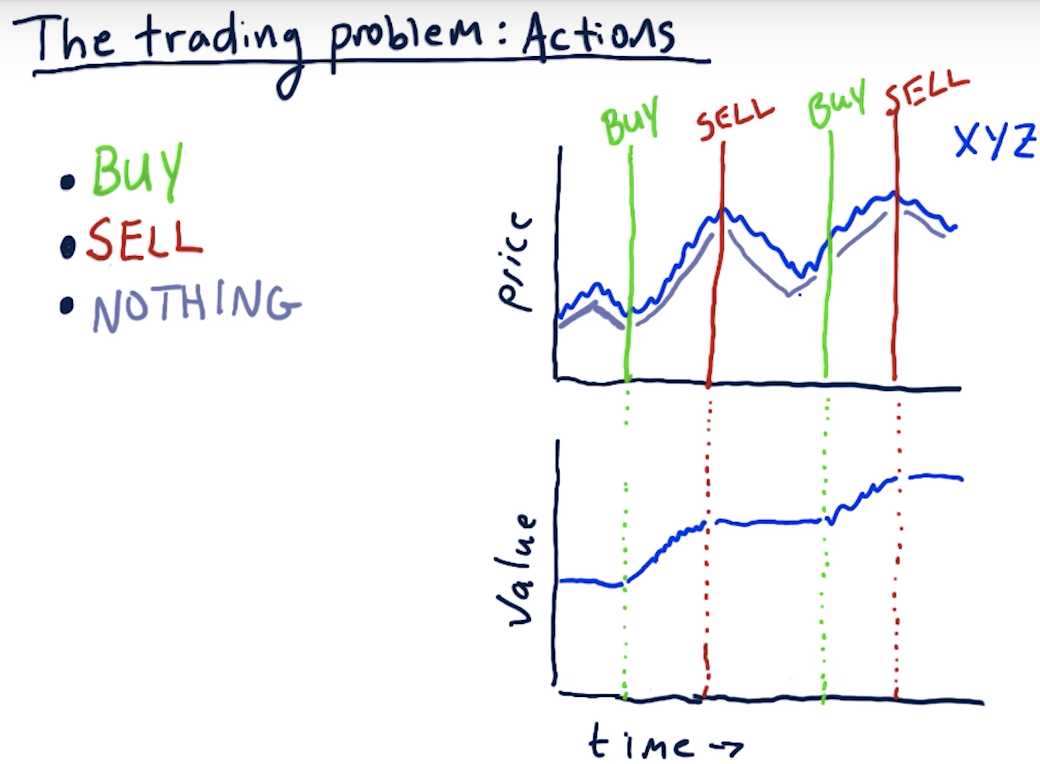

A reward at each step allows the learning agent get feedback on each individual action it takes (including doing nothing).

SMA: single moving average => different stocks have different basis
=> adj close / SMA is a good normalized factor
Creating the State
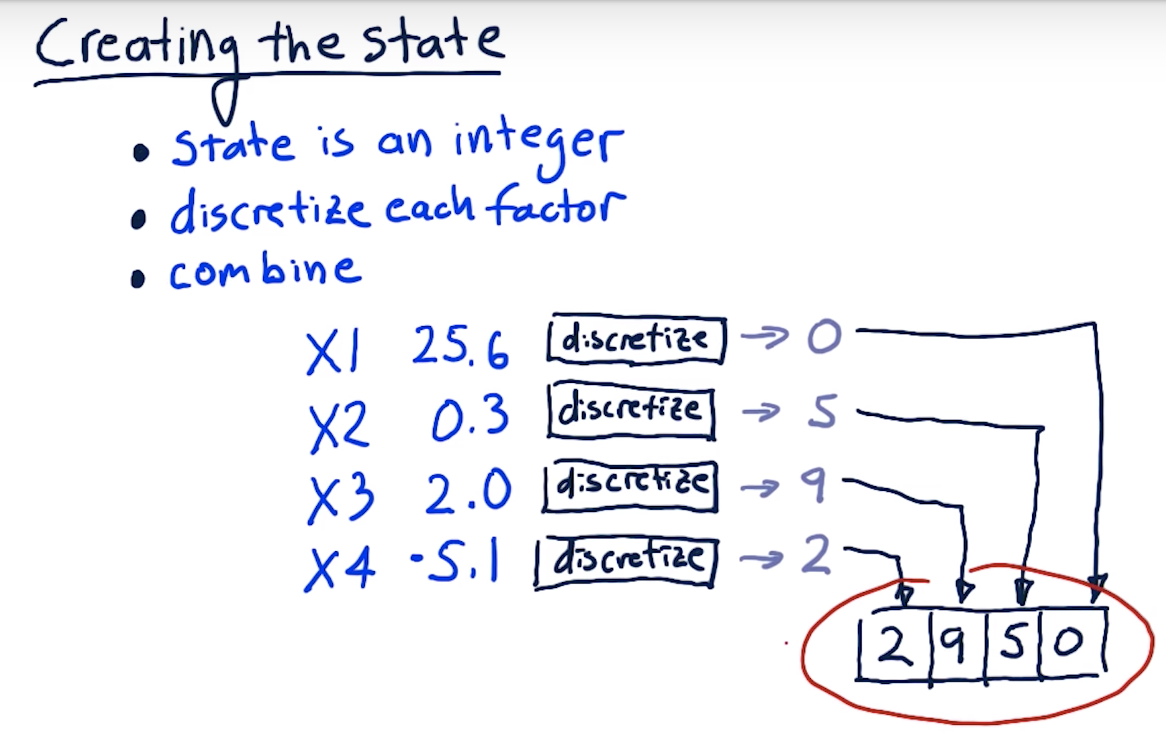
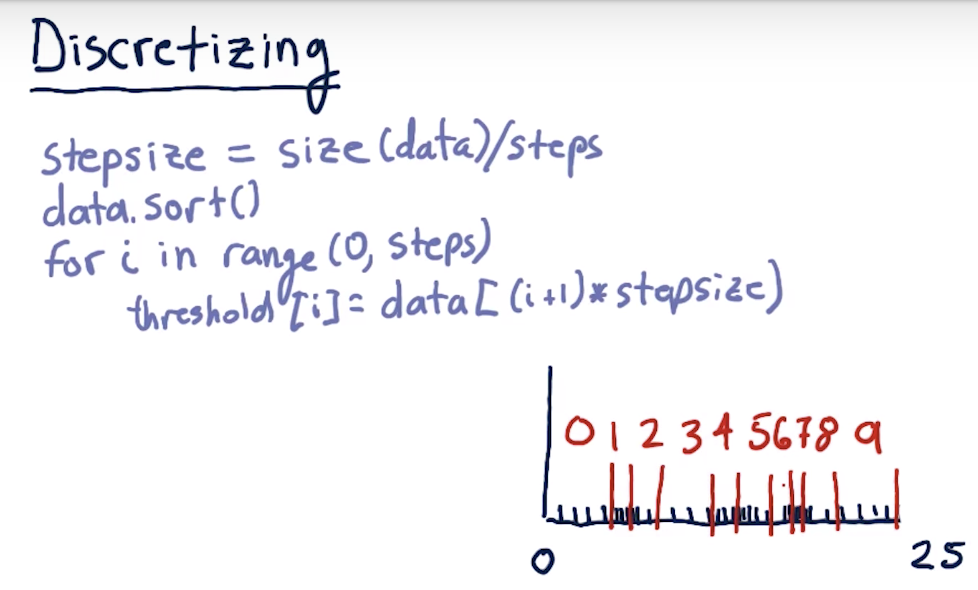
Discretizing
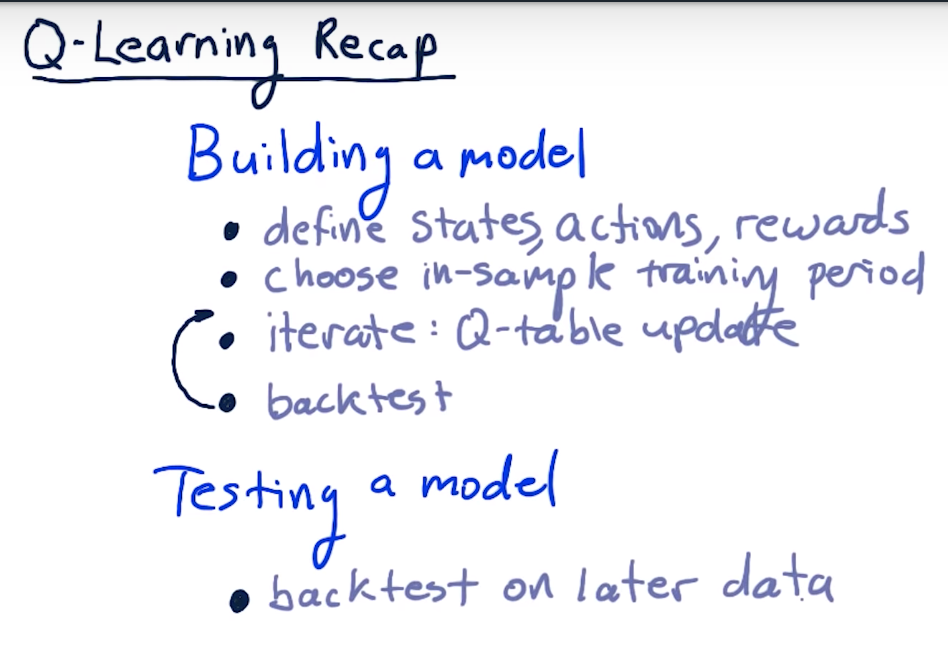
Q-Learning Recap
Summary
Advantages
- The main advantage of a model-free approach like Q-Learning over model-based techniques is that it can easily be applied to domains where all states and/or transitions are not fully defined.
- As a result, we do not need additional data structures to store transitions
T(s, a, s')or rewardsR(s, a). - Also, the Q-value for any state-action pair takes into account future rewards. Thus, it encodes both the best possible value of a state (
maxa Q(s, a)) as well as the best policy in terms of the action that should be taken (argmaxa Q(s, a)).
Issues
- The biggest challenge is that the reward (e.g. for buying a stock) often comes in the future - representing that properly requires look-ahead and careful weighting.
- Another problem is that taking random actions (such as trades) just to learn a good strategy is not really feasible (you'll end up losing a lot of money!).
- In the next lesson, we will discuss an algorithm that tries to address this second problem by simulating the effect of actions based on historical data.
Resources
- CS7641 Machine Learning, taught by Charles Isbell and Michael Littman
- Watch for free on Udacity (mini-course 3, lessons RL 1 - 4)
- Watch for free on YouTube
- Or take the course as part of the OMSCS program!
- RL course by David Silver (videos, slides)
- A Painless Q-Learning Tutorial
Dyna-Q Big Picture <= invented by Richard Sutton
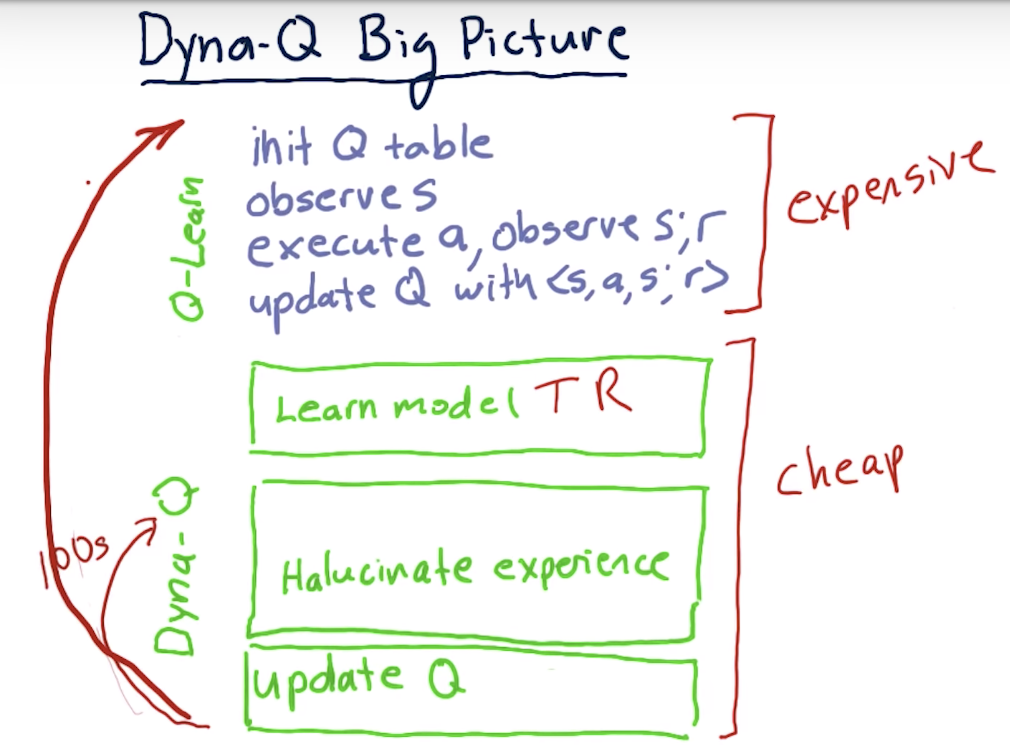

Learning T

How to Evaluate T?

Type in your expression using MathQuill - a WYSIWYG math renderer that understands LaTeX.
E.g.:
- to enter
Tc, type:T_c - to enter
Σ, type:Sigma
For entering a fraction, simply type / and MathQuill will automatically format it. Try it out!
Correction: The expression should be: In the denominator shown in the video,
In the denominator shown in the video, T is missing the subscript c.
Learning R

Dyna Q Recap

Summary
The Dyna architecture consists of a combination of:
- direct reinforcement learning from real experience tuples gathered by acting in an environment,
- updating an internal model of the environment, and,
- using the model to simulate experiences.

Sutton and Barto. Reinforcement Learning: An Introduction. MIT Press, Cambridge, MA, 1998. [web]
Resources
- Richard S. Sutton. Integrated architectures for learning, planning, and reacting based on approximating dynamic programming. In Proceedings of the Seventh International Conference on Machine Learning, Austin, TX, 1990. [pdf]
- Sutton and Barto. Reinforcement Learning: An Introduction. MIT Press, Cambridge, MA, 1998. [web]
- RL course by David Silver (videos, slides)
- Lecture 8: Integrating Learning and Planning [pdf]
Interview with Tammer Kamel
Tammer Kamel is the founder and CEO of Quandl - a data platform that makes financial and economic data available through easy-to-use APIs.
Listen to this two-part interview with him.
Note: The interview is audio-only; closed captioning is available (CC button in the player).