题目描述

输入输出格式
输入格式: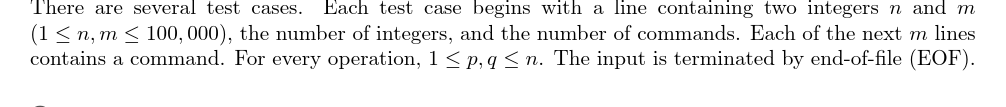
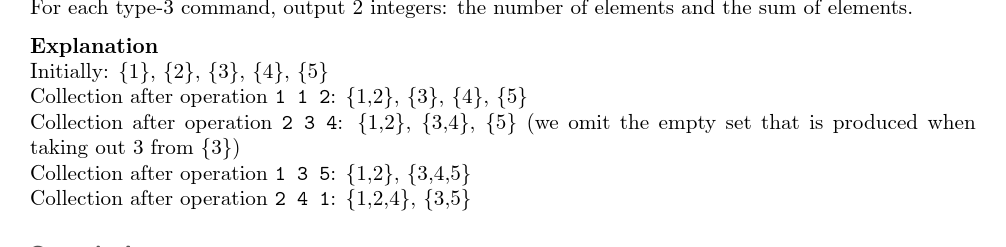
输入输出样例
输入样例#1:
5 7
1 1 2
2 3 4
1 3 5
3 4
2 4 1
3 4
3 3
输出样例#1:
3 12
3 7
2 8
Solution:
本题平衡树。
考试的时候想到的就是无旋treap了,正解貌似是并查集(我没想出来,太菜了)。
节点维护子树大小和子树和,开始时每个节点就是一棵treap,因为我们并不要保证有序,所以可以直接按中序遍历维护,合并分离就不需要考虑优先级了。
对于操作一,若不在同一棵树中,直接merge两棵树。
对于操作二,因为随机键值树高为$log n$,所以直接暴力往上跳到$x$所在树的根,跳的同时求出$x$在该树中的排名,若$x,y$不在同一棵树中,按排名将$x$分离出来,与$y$所在树合并。
对于操作三,直接找到$x$所在树根输出子树大小和子树和就好了。
代码:
/*Code by 520 -- 10.24*/ #include<bits/stdc++.h> #pragma GCC optimize(2) #define il inline #define ll long long #define RE register #define For(i,a,b) for(RE int (i)=(a);(i)<=(b);(i)++) #define Bor(i,a,b) for(RE int (i)=(b);(i)>=(a);(i)--) using namespace std; const int N=100005; int n,m,ch[N][2],rnd[N],siz[N],date[N],cnt,fa[N],sum[N]; int gi(){ int a=0;char x=getchar(); while(x<'0'||x>'9') x=getchar(); while(x>='0'&&x<='9') a=(a<<3)+(a<<1)+(x^48),x=getchar(); return a; } il void newnode(int v){ ++cnt; ch[cnt][0]=ch[cnt][1]=0,sum[cnt]=v; siz[cnt]=1,date[cnt]=v,rnd[cnt]=rand(),fa[cnt]=0; } il void up(int rt){ if(ch[rt][0]) fa[ch[rt][0]]=rt; if(ch[rt][1]) fa[ch[rt][1]]=rt; siz[rt]=siz[ch[rt][0]]+siz[ch[rt][1]]+1; sum[rt]=sum[ch[rt][0]]+sum[ch[rt][1]]+date[rt]; } int merge(int x,int y){ if(!x||!y) return x+y; if(rnd[x]<rnd[y]) {ch[x][1]=merge(ch[x][1],y),up(x);return x;} else {ch[y][0]=merge(x,ch[y][0]),up(y);return y;} } void split(int rt,int v,int &x,int &y){ if(!rt) {x=y=0;return;} if(siz[ch[rt][0]]>=v) y=rt,split(ch[rt][0],v,x,ch[y][0]),up(y); else x=rt,split(ch[rt][1],v-siz[ch[rt][0]]-1,ch[x][1],y),up(x); } int find(int x,int &tot){ if(!fa[x])return x; if(ch[fa[x]][1]==x) tot+=siz[ch[fa[x]][0]]+1; return find(fa[x],tot); } int main(){ srand(time(0)); while(scanf("%d%d",&n,&m)!=EOF){ cnt=0; int opt,a,b,c,x,y,z; For(i,1,n) newnode(i); while(m--){ opt=gi(),a=gi(); if(opt==1){ b=gi(); a=find(a,x=0),b=find(b,x=0); if(a!=b) merge(a,b); } else if(opt==2){ int k=siz[ch[a][0]]+1; b=gi();c=find(a,k),b=find(b,opt); if(c!=b){ x=y=z=0; split(c,k,x,y),split(x,k-1,x,z),x=merge(x,y),b=merge(b,z); fa[x]=0,fa[b]=0; } } else { a=find(a,x=0); printf("%d %d ",siz[a],sum[a]); } } } return 0; }