PKU 2352 Stars(裸一维树状数组)

题目大意：原题链接

就是求每个小星星左小角的星星的个数。坐标按照Y升序，Y相同X升序的顺序给出
由于y轴已经排好序，可以按照x坐标建立一维树状数组

关键是要理解树状数组中的c[maxn]数组的构成方式，例如c1=a1,c2=c1+a2,c3=a3,c4=c2+c3+a4,c5=a5,

c6=c5+a6,c7=a7,c8=c4+c6+c7+a8......

(可以发现当c[maxn]数组的下标为2的幂次方时,c[n]则为数组a[maxn]的前n项和)

具体请看树状数组的构成图

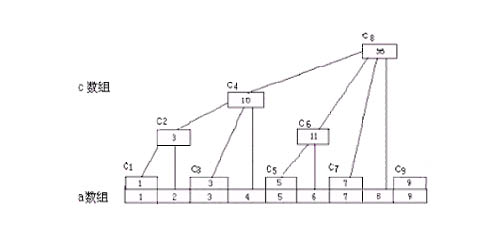
Sum(int i)表示对a[maxn]数组元素的求前i项和

#include<cstdio>
#include<cstring>
using namespace std;
int c[32010];
int cnt[15010];
int lowbit(int x)
{
    return x&(-x);
}
void Add(int i,int val)
{
    while(i<=32010){
        c[i]+=val;
        i+=lowbit(i); 
    }//i为下一个管辖i在内且即将要修改的c[maxn]数组元素下标
}
//返回s为横坐标为i的左下方的星星个数之和(同时也是该星星级数)
int Sum(int i) 
{
    int s=0;
    while(i>0){
        s+=c[i]; 
        i-=lowbit(i);//i减掉自己管辖在内的星星数 
    }//i为下一个虽不被i管辖却即将要加和的c[maxn]数组元素下标
    return s;
}
int main()
{
    int n,x,y;
    while(scanf("%d",&n)!=EOF){
        memset(c,0,sizeof(c));
        memset(cnt,0,sizeof(cnt));
        for(int i=0;i<n;i++){
            scanf("%d%d",&x,&y);
            int t=Sum(x);//+1是为了避免x=0,t为级数 
            cnt[t]++;
            Add(x,1);
        }
        for(int i=0;i<n;i++)
             printf("%d
",cnt[i]);
    }
    return 0;
}