广度优先算法描述
(1)给定图G=<V,E>和一个可以识别的源结点s,广度优先搜索对图G中的边进行系统性的探索来发现可以从源结点到达所有节点的路径。该算法能够计算出从源结点s到每个可到达的结点的距离,同时生成一颗广度优先搜索树。该数已源结点s为根节点,包含所有的可能从s到达的点。对于每一个从源结点s可以达到的jiedianv,在广度优先搜索树里面从结点s到达结点v的简单路径对应的就是s到v的最短路径。
(2)下面结合例子看一下广度优先搜索的具体流程。例子中,每一个结点可能被置为白色、灰色或者黑色。最开始的时候,所有的结点都被置为白色。在算法一步步执行过程中,这些结点可能变为灰色或者黑色。搜索过程中,结点第一次被遇到就称结点被发现,此时结点的颜色将发生改变。因此,凡是灰色或者黑色的结点都是一被发现的结点。除此之外,广度优先搜索将灰色和黑色结点加以区别,以此确保搜索按照广度优先进行。(如果变<u,v>∈E且结点u是黑色,那么与结点u相连的结点v可能是灰色,也可能是黑色。也就是说,所有与黑色结点相连的结点可能是黑色或者灰色,都已被发现。所有与灰色结点相连的结点可能是白色,换而言之,灰色结点代表的就是已知和未知两个集合的边界)。
(3)广度优先搜索的算法描述
1 BFS(G,s)
2 for each vertex u∈G.V-{s}
3 u.color = WHITE
4 u.d = ∞
5 u.π = NIL
6 s.color = GRAY
7 s.d = 0
8 s.π = NIL
9 Q = ∅
10 ENQUEUE(Q,s)
11 while(Q ≠ ∅)
12 u = DEQUEUE(Q)
13 for each v ∈ G.Adj[u]
14 if v.color == WHITE
15 v.color = GRAY
16 v.d = u.d + 1
17 v.π = u
18 ENQUEUE(Q,v)
19 u.color = BLACK
(4)如图所示是一个BFS的过程
①初始时候,将源结点s置为灰色,并且加入集合Q中,Q是一个先进先出的队列,如图所示
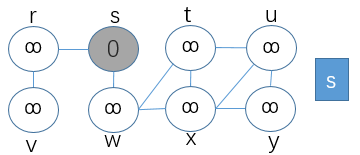
②第二步,将s结点置为黑色,并出队列,同时与之相连的r和w结点置为灰色,并加入队列中,更新r、w结点的路径距离
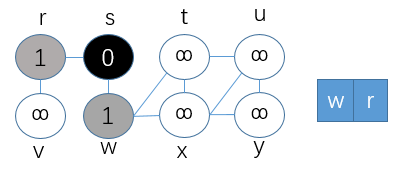
③第三步,将w置为黑色,并出队列,同时将与之相连的t和x结点置为灰色,加入队列中,更新t、x结点的路径距离
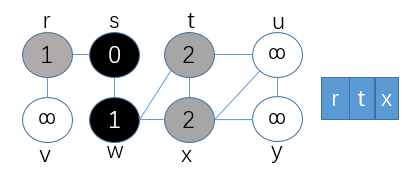
④第四步,将r结点置为黑色,并出队列,同时将与之相连的v结点置为灰色,加入队列中,跟新结点v的路径距离
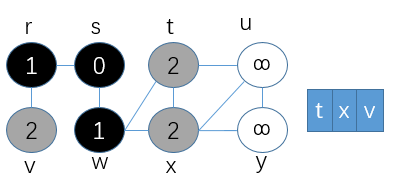
⑤第五步,将t结点置为黑色,并出队列,同时将与其相连的结点u置为灰色,加入队列中,更新结点u的路径距离
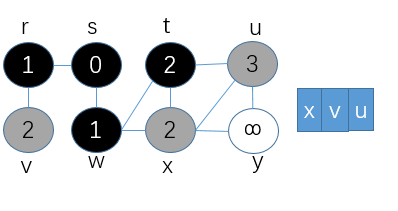
⑥第六步,将x结点置为黑色,并出队列,同时将与之相连的结点y置为灰色,加入队列中,更新结点y的路径距离

⑦第七步,将结点v置为黑色,出队列

⑧第八步,将结点u置为黑色,出队列

⑨将最后一个结点y置为黑色,出队列,此时队列为空Q=∅
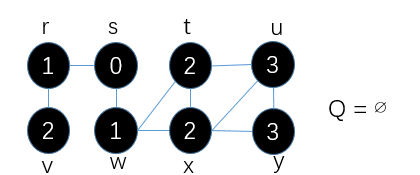
(5)下面分析一下伪代码
除了源结点之外,算法的2~5行是将所有结点在初始情况下涂为白色,将每个结点值距离属性置为∞,将每个结点的父节点设置为NIL。第6行将源结点s置为灰色,这是默认的初始情况,表示从源结点开始搜索。第9~10行对队列Q进行初始化,因为在初始时刻,队列中只有源结点s。
算法第11~19行的while循环一直执行,知道图中不再有灰色结点为止。即Q=∅
最短距离
(1)给定G=<V,E>,G为一个有向图或者无向图,设s∈V为任意结点,则对于任意边<u,v>∈E,σ(s,v)≤σ(s,u)+1
简单证明一下:如果结点u是可以从结点s到达的结点,则结点v也是必然可以从s到达的结点。在这种情况下,从源结点s到结点v的最短路径距离不可能比s到u的最短距离加上边(u,v)更长。由此可以得出结论。
(2)设G=<V,E>为一个有向图或者无向图,假定BFS以给定结点s∈V作为源结点在图G上,则在BFS结束的时候,对于每一个结点v∈V,BFS所计算出的v.d满足v.d≥σ(s,v)
简单证明一下:BFS归结出的算法中,通过对算法里面的入队列ENQUEUE操作的次数进行数学归纳来总结这个定理。
归纳假设是:对于所有结点v∈V,v.d≥σ(s,v)
归纳的基础是BFS在将源结点加入Q之后开始。这时候,s.d=0 == σ(s,s),并且此时对于其他节点的d=∞显然大于σ(s,v),所以归纳假设成立
对于归纳步,表示为从结点u进行邻接链表搜索时发现的白色结点v。有归纳假设得到u.d≥σ(s,u)。由算法v.d = u.d + 1和上面(1)可知,v.d = u.d + 1≥σ(s,u)+1≥σ(s,v)。除此之外,因为结点v被加入到队列之后会被置为灰色,不会再一次入队列,所以此时得到的v.d不会变化