二维的NS-方程:
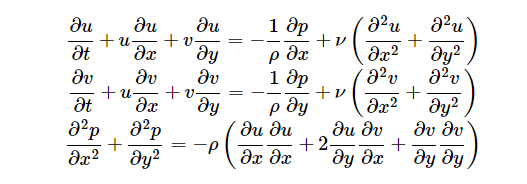
这个方程一定要拆分成部分才能解出来。
这里面我感觉只要把泊松方程解法搞定,基本快出山写最简单的 "计算流体" 完全没问题
以下是做了个初始的source field,用python numpy 先快速撸了一遍算法。

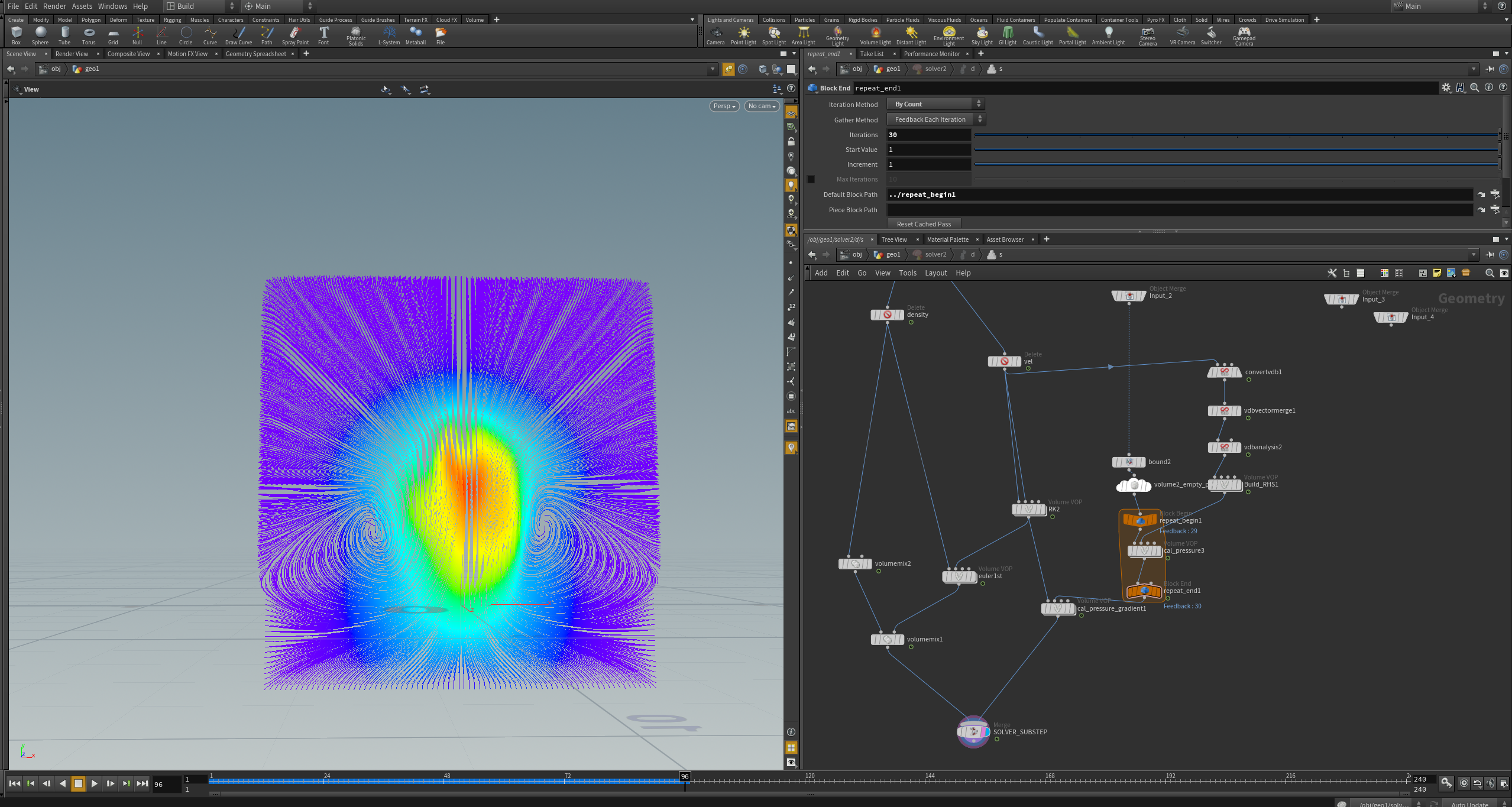
并且重新实现3d版本在Houdini中,houdini有更好的可视化.
velocity advection 是RK2,
density advection 一阶的,
然后发现density field确实跟不上velocity field
从零蛋编写无粘流体最简单的路线:
<0>为什么要使用MAC-GRID:
按照作者的说法,使用这种grid,最大的优势是解决了中心差分法零空间问题。
速度场一定要存在face center.
所以在Houdini看vel field 是一定存在grid face center上的,而不是grid cell center!
而density,temperature....这类场是存在grid cell上的。
总结下一个inviscid fluid(欧拉无粘流体)实现过程:
<1>对流。
最重要的是理解材质导数.为什么这个玩意能等于0? 详见欧拉与拉格朗日的观点。

这个差分法是万万不可取,因为会出现null-space,试着想想如果有3个点,中间的点高一点,两边一样高,那么用中心差分法算出来中间点的斜率将是0.
所以使用无条件稳定的 半拉格朗日,这个其实完全是解ODE问题了。而不是PDE了
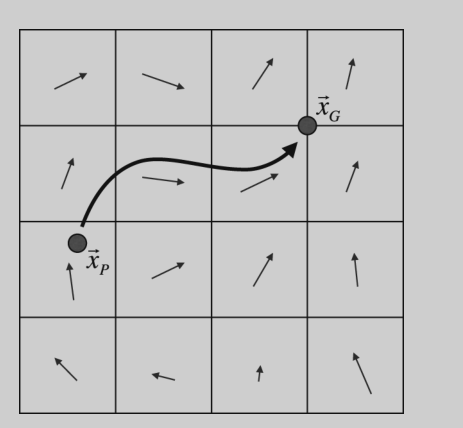
比如要得到xp的值,只需用用 向前euler 向后追踪法。当然这个方法比较废物。作者推荐RK家族的算法比如:RK2:
def RK2(x, y, dt, ugrid, vgrid): nu = neibours_value(ugrid, x, y, "u") nv = neibours_value(vgrid, x, y, "v") xmid = x - 1.0 / 2.0 * dt * nu ymid = y - 1.0 / 2.0 * dt * nv umid = neibours_value(ugrid, xmid, ymid) vmid = neibours_value(vgrid, xmid, ymid) x -= dt * umid y -= dt * vmid return (x, y)
(你去看houdini上面的gas advect 还有RK5)

得到位置直接用bilerp()插值法求出xp的量。
def bilerp(f00, f10, f01, f11, tx, ty): """ FIGURE : first lerp in top x,then bottom x, then along y axis f00*----------.tx-----------*f10 | | | | | | | .ty | | | | | | | f01*----------.tx-----------*f11 """ return lerp(lerp(f00, f10, tx), lerp(f01, f11, tx), ty)
那么这个量就是作为下一个时间步的量。
测试这个最简单的就是创建一个简单的恒定区域网格速度,然后让自己的初始的density是不是根据semi-lagrangian方法能advection.
<1.1>推出压力方程:
梯度压力方程:

离散,下面有具体的压力梯度离散过程。
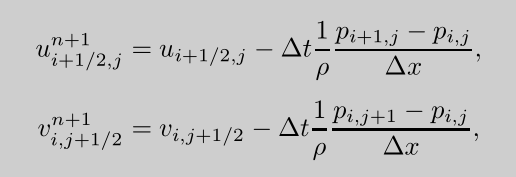
这个为压力梯度方程。只要求出压力p就可以得到无散速度场。
接下来不可压缩流体条件:
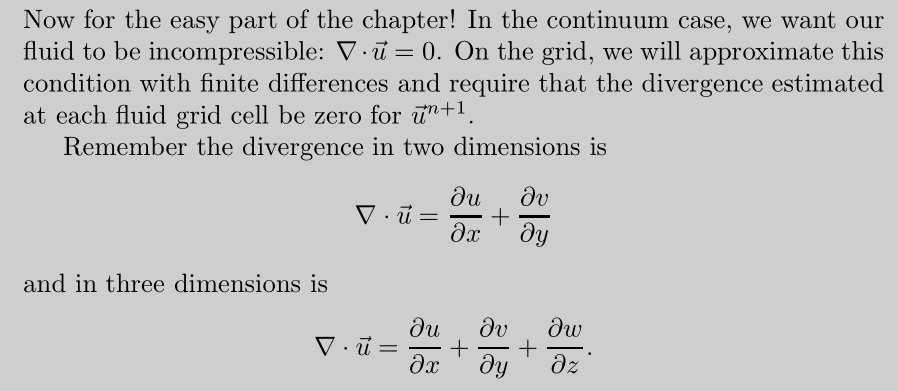
使用中心差分法离散。这样没有null-space,因为速度场特殊的储存方式

接下来推出怎么样得到下一个时间步上的流体速度场是无散度,这里有个技巧,我们不能直接使用5.4式。但是:
首先把速度散度公式写成下一步时间的离散形式:
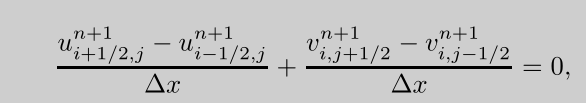
把梯度压力方程带入可以得到:
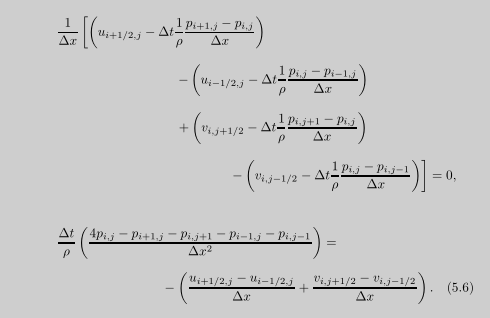
观察此方程,右边就是不可压缩 负的速度梯度, 这部分叫做rhs,右手方程,这个是已知的。
所以方程中只有压力p未知。求出压力p即可。
<2>求压力右手方程。通常就叫做RHS,就是负的速度场的散度。-divergence(u)
这个是简单的。

<3>求解压力.
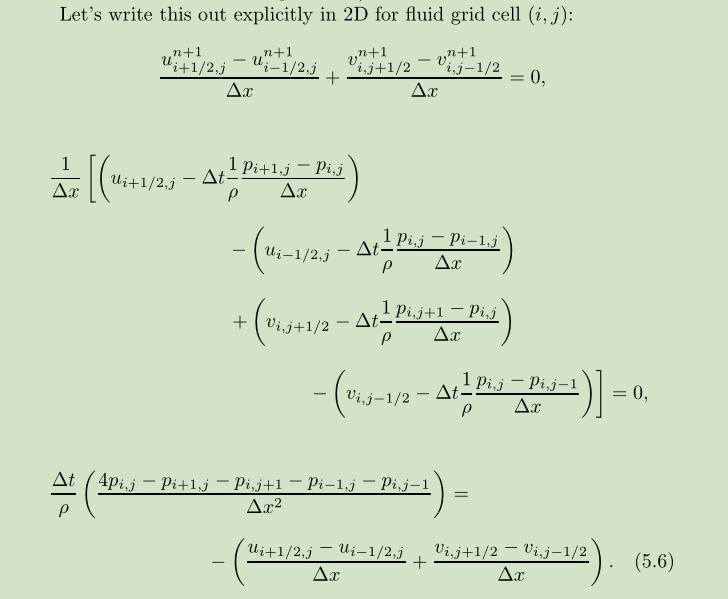

这个有好多方法求,由于是一个AX=b 的形式,大部分文章是以PCG/GAUSS-SEIDEI/GAUSS-SEIDEI SOR/JACOBI方式
由于在numpy方便,我直接把方程用切片法做了。
<4>把求的pressure field 带入压力梯度更新方程,求出无散度的速度。
Pressure gradient 压力梯度方程离散:
这个方程我觉得才是套路中的套路。有了这个压力,直接带入这个公式 ,就可以求出无散的流体。
