牛客小白月赛33全题解

小白月赛33题解(全)

A.字符统计

题目链接：https://ac.nowcoder.com/acm/contest/11210/A

直接读入字符串进行遍历即可。用getline()读一行字符串，注意：cin读入后的回车会留在输入缓冲区，getline()的不会，所以在使用cin后，getline()之前需要清空输入缓冲区

注意行开头空格和空行的特殊处理。

AC代码：

#include <iostream>

using namespace std;

string s;
int r, dc, zf;

int main()
{
    int t;
    cin >> t;
    getline(cin, s);
    
    while(t--)
    {
        r = dc = zf = 0;
        while(getline(cin, s) && s != "=====")
        {
            r++;
            for(int i = 0; i < s.size(); i++)
            {
                if(s[i] == ' ' && i) dc++;
                zf++;
            }
            if(s.size())dc++;
        }
        cout << r << ' ' << dc << ' ' << zf << endl;
    }
    
    return 0;
}

B.连分数

题目链接：https://ac.nowcoder.com/acm/contest/11210/B

对一般的(p/q)，(p / q = a + 1 / m, 其中m = q / (p \% q))，然后令分子 = q, 分母 = p % q，继续上述操作，直到$ p % q == 0$时结束操作。

细节处理：

1. 没输出一个a，如果p、q更新后可以进行操作，则输出“+1/{”，并且记录输出的’{‘的数量
2. 如果p、q更新后不可进行操作，即(p \% q == 0)，则说明到最后一个数了，不用输出大括号，并且下一轮会结束循环
3. 最后输出等量的’}‘。

AC代码：

#include <iostream>
#include <cstdio>

using namespace std;

int t, p, q;

int main()
{
    cin >> t;
    
    while(t--)
    {
        scanf("%d%d", &p, &q);
        printf("%d/%d = ", p, q);
        int kh = 0;
        while(q)
        {
            printf("%d", p / q);
            int t = p % q;
            p = q, q = t;
            if(q)
            {
                if(p % q != 0)
                {
                    printf("+1/{");
                    kh++;
                }
                else printf("+1/");
            }
        }
        while(kh--) printf("}");
        puts("");
    }
    return 0;
}

C.挪酒瓶

题目链接：https://ac.nowcoder.com/acm/contest/11210/C

参考题解：https://www.nowcoder.com/discuss/643079、https://blog.nowcoder.net/n/efd1e10b345a42e1ae0231fc4ae9e7b4

对于一个有 n 个元素的置换群p，从最后一个 a往前开始换，则费用为 ((w_a+w_b)+(w_a+w_c)+...=(n−2)w_a+sum_{iin p}w_i)

最优的策略则是选择较小的 (w_a) 开始换。

对于多个置换群而言，单独内部交换并不是最优解，可以把目前最轻的酒瓶拿进来替换，最后再换回去。令置换群 p 内最轻重量为 (m_p=min_{iin p}wi)，令全部的酒里面最轻重量为 (m_{all})。这个策略的花费为 (2(m_{all}+m_p)+(n−2)m_{all}+sum_{iin p}w_i - m_p + m_{all})(交换两次最小值花费：(2(m_{all}+m_p))，交换后的所有费用和为：(sum_{iin p}w_i - m_p + m_{all}))

最后对于每一个置换群，考虑两个 Case 如下，都选择最优即可：

• ((n−2)w_p+sum_{iin p}w_i)
• (2(m_{all}+m_p)+(n−2)m_{all}+∑_{iεp}w_i - m_p + m_{all}) = ((n + 1)*m_{all} + m_p + sum_{iin p}w_i)

AC代码：

#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;

const int N = 1e5+10;

int a[N], w[N];
bool st[N];

int main()
{
    int t;
    cin >> t;
    while(t--)
    {
        memset(st, 0, sizeof st);
        int n, ans = 0, min_all = 1e9;
        cin >> n;
        for(int i = 1; i <= n; i++) scanf("%d", &a[i]);
        for(int i = 1; i <= n; i++)
        {
            scanf("%d", &w[i]);
            //找出全局最小值
            min_all = min(min_all, w[i]);
        }
        
        for(int i = 1; i <= n; i++)
            if(!st[i])
            {
                int cnt = 0, minv = 1e9;
                //求一个置换群
                for(int j = i; !st[j]; j = a[j])
                {
                    cnt++;
                    ans += w[j];
                    minv = min(minv, w[j]);
                    st[j] = true;
                }
                //最优解更新
                ans += min((cnt - 2) * minv, (cnt + 1) * min_all + minv);
            }
        cout << ans << endl;
    }
    
    return 0;
}

D.购物

题目链接：https://ac.nowcoder.com/acm/contest/11210/D

将物品名称映射到数字，用数组记录每一个物品的数量，然后遍历每个人，将其没有的物品的数量-1，最后遍历计算物品数量大于0的个数。

AC代码：

#include <iostream>
#include <algorithm>
#include <unordered_map>
#include <cstring>

using namespace std;

const int N = 110;

int t, s, n;
int a[N];

int main()
{
    cin >> t;
    
    while(t--)
    {
        memset(a, 0, sizeof a);
        unordered_map<string, int> goods;
        string str;
        int x, idx = 0;
        scanf("%d%d", &s, &n);
        for(int i = 0; i < s; i++)
        {
            cin >> str >> x;
            goods.insert({str, idx++});
            a[goods[str]] = x;
        }
        //for(int i = 0; i < idx; i++) cout << a[i] << ' ';
        //puts("");
        for(int i = 0; i < n; i++)
        {
            bool has[N];
            memset(has, false, sizeof has);
            cin >> x;
            for(int j = 0; j < x; j++)
            {
                cin >> str;
                has[goods[str]] = true;
            }
            for(int i = 0; i < idx; i++)
                if(!has[i]) a[i]--;
        }
        int ans = 0;
        for(int i = 0; i < idx; i++)
            if(a[i] > 0) ans++;
        if(ans) cout << ans << endl;
        else puts("Need to be lucky");
    }
    return 0;
}

E.喝可乐

题目链接：https://ac.nowcoder.com/acm/contest/11210/E

直接枚举每种可乐买多少瓶的所有情况，对每种情况计算能喝到的瓶数，记录最大值即可。

AC代码：

#include <iostream>
#include <algorithm>

using namespace std;

int t, n, a, b;

int main()
{
    cin >> t;
    while(t--)
    {
        int ans = 0;
        cin >> n >> a >> b;
        for(int i = 0; i <= n; i++)
        {
            int Max = n, an = i, bn = n - i;
            while(an >= a || bn >= b)
            {
                if(an >= a)
                {
                    Max += an / a;
                    bn += an / a;
                    an = an % a;
                }
                if(bn >= b)
                {
                    Max += bn / b;
                    an += bn / b;
                    bn = bn % b;
                }
            }
            ans = max(Max, ans);
        }
        cout << ans << endl;
    }
    return 0;
}

F.天旋地转

题目链接：https://ac.nowcoder.com/acm/contest/11210/F

模拟，把坐标系的四种不同情况下的移动偏移量存下来，然后按步骤一步一步操作即可。

注意在计算逆时针旋转时，标记坐标轴方向的数字fx需要变为非负数

AC代码：

#include <iostream>
#include <algorithm>
#include <unordered_map>

#define x first
#define y second;

using namespace std;

typedef long long LL;
typedef pair<int, int> PII;

int t, n;
PII Move[4][4] = {{{0, 1}, {-1, 0}, {1, 0}, {0, -1}},
{{-1, 0}, {0, -1}, {0, 1}, {1, 0}},
{{0, -1}, {1, 0}, {-1, 0}, {0, 1}},
{{1, 0}, {0, 1}, {0, -1}, {-1, 0}}};
unordered_map<char, int> f {{'w', 0}, {'a', 1}, {'d', 2}, {'s', 3}};

int main()
{
    cin >> t;
    while(t--)
    {
        LL xx = 0, yy = 0, fx = 0, k;
        cin >> n;
        while(n--)
        {
            char c;
            cin >> c >> k;
            if(c == 'r') fx = (fx + k) % 4;
            else if(c == 'l') fx = ((fx - k) % 4 + 4) % 4;
            else xx += k * Move[fx][f[c]].x, yy += k * Move[fx][f[c]].y;
            //cout << fx << ' ' << xx << ',' << yy << endl;
        }
        cout << xx << ' ' << yy << endl;
    }
    return 0;
}

G.切圈圈

题目链接：https://ac.nowcoder.com/acm/contest/11210/G

首先预处理出前缀和数组。可以知道性质：前缀和数组中相等的两点，之间的区间和一定是0。题目已经给出整个数组的和为0，那么只要确定数组中的一段和为0的区间，则另外一段（包含首尾的那一段）也就一定区间和为0了。所以可以直接在一维线性结构上进行求解。

当已经确定了一个区间和为0的区间时，这区间的端点前缀和数组的值一定相等。如果该区间内可以再分，由性质可得，区间内的切分点的前缀和数组值一定和两个端点的值相等。（环的另外一段也是如此）

由此可以进一步推出：最后分割出来的区间，所有端点的前缀和数组值一定相等。

所以，只要求出前缀和数组值相等的最大数量，即为答案。

AC代码：

#include <iostream>
#include <algorithm>
#include <map>

using namespace std;

const int N = 10010;

int t, n;
int a[N];

int main()
{
    cin >> t;
    while(t--)
    {
        cin >> n;
        int ans = 0;
        map<int, int> m;
        for(int i = 1; i <= n; i++)
        {
            scanf("%d", &a[i]);
            //预处理前缀和数组
            a[i] += a[i - 1];
            //记录值为a[i]的点有多少个
            m[a[i]]++;
            ans = max(ans, m[a[i]]);
        }
        cout << ans << endl;
    }
    return 0;
}

H.货物运输

题目链接：https://ac.nowcoder.com/acm/contest/11210/H

根据题目建有向图，然后直接套最短路模板即可。

关于建图，难点在处理好边权：

边权：w[i] = c * min(f, d) + max(0, f - d) * cc

AC代码：

#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;

typedef long long LL;

const int N = 110;

int t, n, m, s, ee, f;
int a, b, c, d, cc;
int h[N], e[N * N], ne[N * N], idx;
LL w[N * N], dist[N];
bool st[N];

void add(int a, int b, LL c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}

void dij(int u)
{
    dist[u] = 0;
    
    for(int i = 0; i < n; i++)
    {
        int k = -1;
        for(int j = 1; j <= n; j++)
            if(!st[j] && (k == -1 || dist[k] > dist[j]))
                k = j;
        
        for(int j = h[k]; j != -1; j = ne[j])
        {
            dist[e[j]] = min(dist[e[j]], dist[k] + w[j]);
        }
        
        st[k] = true;
    }
}

int main()
{
    cin >> t;
    while(t--)
    {
        idx = 0;
        memset(h, -1, sizeof h);
        memset(dist, 0x3f, sizeof dist);
        memset(st, false, sizeof st);
        scanf("%d%d%d%d%d", &n, &m, &s, &ee, &f);
        for(int i = 0; i < m; i++)
        {
            scanf("%d%d%d%d%d", &a, &b, &c, &d, &cc);
            //注意d、f的大小
            add(a, b, (LL)c * min(d, f) + (LL)max(0, f - d) * cc);
        }
        dij(s);
        //for(int i = 1; i <= n; i++)
        //    cout << i << ':' << dist[i] << endl;
        printf("%lld
", dist[ee]);
    }
    
    return 0;
}

I.三角尼姆

题目链接：https://ac.nowcoder.com/acm/contest/11210/I

首先手动模拟发现：N = 1时Alice必赢，此时一共有1个空位；N = 2时Alice必赢，此时一共有3个空位；N = 3时Bob必赢，此时一共有6个空位；N = 4时Bob必赢，此时一共有10个空位。。。。。。

大胆猜测出：当空位总数为偶数个是，先手必赢，否则先手必输

经代码检验猜测正确。

证明：最后输的条件一定是只剩1个空位，往前推一下就是倒数第二次放棋子一定是3个空位，即最后面对的必输局面是剩下奇数个空位。

由：奇数 - 奇数 = 偶数，偶数 - 奇数 = 奇数，且每次减少空位一定是1或者3（奇数）

可得：剩余空位数一定是以“奇偶奇偶...”或者“偶奇偶奇...”的顺序出现的

进一步可得：如果玩家第一次面对的是偶数个空位，则一直是面对偶数个空位，则一定不会碰到奇数的情况，就一定不会输

AC代码：

#include <iostream>
#include <algorithm>

using namespace std;

int t, n;

int main()
{
    cin >> t;
    while(t--)
    {
        cin >> n;
        n = (1 + n) * n / 2;
        if(n & 1) puts("Alice");
        else puts("Bob");
    }
    return 0;
}

J.线段的交

题目链接：https://ac.nowcoder.com/acm/contest/11210/J

分两步：判断线段是否相交、求面积。

解法一：利用向量叉积判断线段相交及求四边形面积。

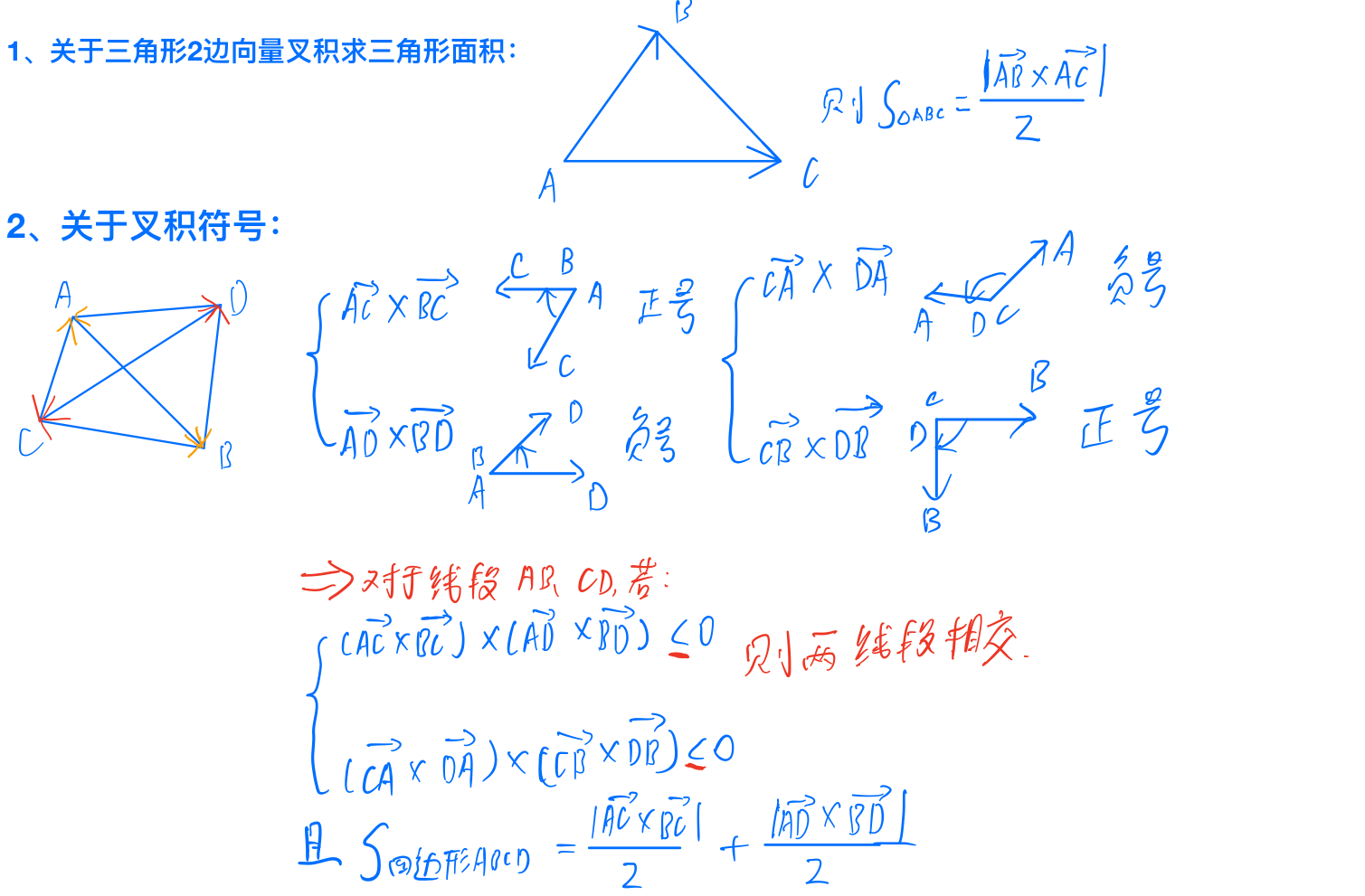
AC代码：

#include <iostream>
#include <algorithm>
#include <cmath>

using namespace std;

double x1, yy1, x2, y2, x3, y3, x4, y4;

struct Point
{
    double x, y;
}p1, p2, q1, q2;

double cj(Point p, Point q)
{
    return p.x * q.y - q.x * p.y;
}

double area(Point p1, Point p2, Point q1)
{
    Point xl1 = {p2.x - p1.x, p2.y - p1.y};
    Point xl2 = {q1.x - p1.x, q1.y - p1.y};
    return cj(xl1, xl2);
}

int main()
{
    scanf("%lf%lf%lf%lf%lf%lf%lf%lf", &x1, &yy1, &x2, &y2, &x3, &y3, &x4, &y4);
    p1 = {x1, yy1}, p2 = {x2, y2}, q1 = {x3, y3}, q2 = {x4, y4};
    
    double s1 = area(p1, p2, q1);
    double s2 = area(p1, p2, q2);
    double s3 = area(q1, q2, p1);
    double s4 = area(q1, q2, p2);
    if(s1 * s2 <= 0 && s3 * s4 <= 0) printf("%.8f
", (fabs(s1) + fabs(s2)) / 2);
    else cout << 0 << endl;
    
    return 0;
}

解法二：利用快速排斥实验和跨立实验判断直线相交，在用向量叉积求四边形面积

WA代码（case通过率92%，bug未知）：

#include <iostream>
#include <algorithm>
#include <cmath>

using namespace std;

double x1, yy1, x2, y2, x3, y3, x4, y4;

struct Point
{
    double x, y;
}p1, p2, q1, q2;
//快速排斥实验
bool kspc(Point p1, Point p2, Point q1, Point q2)
{
    double minRx = min(p1.x, p2.x), minRy = min(p1.y, p1.y);
    double maxRx = max(p1.x, p2.x), maxRy = max(p1.y, p2.y);
    double minTx = min(q1.x, q2.x), minTy = min(q1.y, q2.y);
    double maxTx = max(q1.x, q2.x), maxTy = max(q1.y, q2.y);
    double minFx = max(minRx, minTx), minFy = max(minRy, minTy);
    double maxFx = min(maxRx, maxTx), maxFy = min(maxRy, maxTy);
    return (minFx <= maxFx && minFy <= maxFy);
}
//求向量叉积
double cj(Point p, Point q)
{
    return p.x * q.y - q.x * p.y;
}
//跨立实验
bool kl(Point p1, Point p2, Point q1, Point q2)
{
    Point xl1 = {p1.x - q1.x, p1.y - q1.y}, xl2 = {q2.x - q1.x, q2.y - q1.y}, xl3 = {p2.x - q1.x, p2.y - q1.y};
    Point xl4 = {q1.x - p1.x, q1.y - p1.y}, xl5 = {p2.x - p1.x, p2.y - p1.y}, xl6 = {q2.x - p1.x, q2.y - p1.y};
    return (cj(xl1, xl2) * cj(xl2, xl3) >= 0 && cj(xl4, xl5) * cj(xl5, xl6) >= 0);
}
//求面积
void area()
{
    /*
    double s1 = fabs(p1.x * p2.y - p2.x * p1.y + p2.x * q1.y - q1.x * p2.y + q1.x * p1.y - p1.x * q1.y) / 2;
    double s2 = fabs(p1.x * p2.y - p2.x * p1.y + p2.x * q2.y - q2.x * p2.y + q2.x * p1.y - p1.x * q2.y) / 2;
    */
    Point xl1 = {p2.x - p1.x, p2.y - p1.y};
    Point xl2 = {q1.x - p1.x, q1.y - p1.y};
    Point xl3 = {q2.x - p1.x, q2.y - p1.y};
    printf("%.8lf
", (fabs(cj(xl1, xl2)) + fabs(cj(xl1, xl3))) / 2);
}

int main()
{
    scanf("%lf%lf%lf%lf%lf%lf%lf%lf", &x1, &yy1, &x2, &y2, &x3, &y3, &x4, &y4);
    p1 = {x1, yy1}, p2 = {x2, y2}, q1 = {x3, y3}, q2 = {x4, y4};
    
    if(kspc(p1, p2, q1, q2) && kl(p1, p2, q1, q2)) area();
    else cout << 0 << endl;
    
    return 0;
}