表达式转换
中缀表达式
我们通常看到的表达式像这样:A*B,很容易知道这是A乘以B,这种操作符介于操作数中间的表示法,称为“中缀”表示法。
但有时候,中缀表示法会引起混淆,如“A+B*C”,是A+B然后再乘以C呢?还是B乘以C再加A呢?
为了解决上面的问题,人们引入了操作符“优先级”的概念来消除混淆,规定高优先级的操作符先计算,相同优先级的操作符从左到右依次计算,这样A+B*C就没有疑义,是A加上B与C的乘积。
同时引入了括号来表示强制优先级,括号的优先级最高,而且在嵌套的括号中,内层的优先级更高。这样(A+B)*C就是A与B的和再乘以C。
虽然人们已经习惯了这种表示法,但计算机处理最好是能明确规定所有的计算顺序,这样无需处理复杂的优先规则。
前缀和后缀表达式
接上面的问题,人们又引入了全括号表达式,即在所有的表达式项两边都加上括号,A+B*C+D,应表示为((A+(B * C))+D)。
那么可否将表达式中操作符的位置稍微移动一下呢?
例如中缀表达式A+B,我们将操作符移到前面,变为“+AB”,或者将操作符移动到最后,变为“AB+”。这样我们就得到了表达式的另外两种表示法:“前缀”和“后缀”表示法。(以操作符相对于操作数的位置来定义)
这样A+BC的前缀表达式为“+ABC”,后缀表达式为“ABC*+”。(为了帮助理解,子表达式加了中划线)。
再来看中缀表达式“(A+B)C”,按照转换的规则,前缀表达式是“ * + ABC”,后缀表达式是“AB+C”。神器的事情发生了,在中缀表达式里必须的括号,在前缀和后缀表达式中消失了?
在前缀和后缀表达式中,操作符的次序完全决定了运算的次序,不再有混淆,所以在很多情况下,表达式的计算机表示都避免用复杂的中缀形式。
目前为止,我们仅手工转换了几个中缀表达式到前缀和后缀的形式,一定得有个算法来转换任意复杂的表达式,为了分解算法的复杂度,我们从“全括号”中缀表达式入手。我们看A+BC,如果写成全括号形式:(A+(B * C)),显示表达了计算次序,我们注意到每一对括号,都包含了一组完整的操作符和操作数,看子表达式(B * C)的右括号,如果把操作符 移动到右括号的位置,替代它,在删除左括号,得到BC*,这个正好把子表达式转换为后缀形式,进一步再把更多的操作符移动到相应的右括号处替代之,再山区左括号,那么整个表达式就完成了后缀表达式的转换。
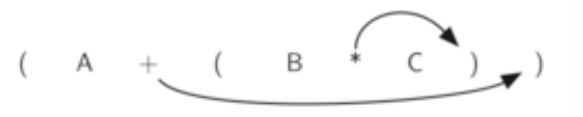
同样的,如果我们把操作符移动到左括号的位置取代之,然后删除所有的右括号,也就得到了前缀表达式。
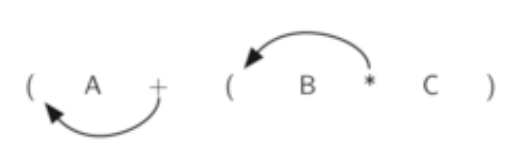
所以说没无论表达式多复杂,需要转换为前缀或者后缀,只需要两步,将中缀表达式转换为全括号形式,将所有的操作符移动到子表达式所在的左括号(前缀)或右括号(后缀)处,再删除所有的括号。
通用的中缀转后缀算法
首先我们来看中缀表达式A+B * C,其对应的后缀表达式是ABC*+,操作数ABC的顺序没有改变,操作符的出现顺序,在后缀表达式中反转了,由于 * 的优先级比 + 高,所以后缀表达式中操作符的出现顺序与运算次序一致。
在中缀表达式转换后缀形式的吹过程中,操作符比操作数要晚输出,所以在扫描到对应的第二个操作数之前,需要把操作符先保存起来,而这些暂存的操作符,由于优先级的规则,还有可能需要反转次序输出,在A + B * C中, + 虽然先出现,但优先级比后面这个* 要低,所以它要等 * 处理完,才能处理。
这种反转特性,我们可以考虑用栈来保存暂时为处理的操作符。
再看看(A + B)* C,对应的后缀形式是 AB + C*,这里+的输出要比 * 要早,主要是因为括号使得 + 的优先级提升,高于括号之外的 *。回顾“全括号”表达式,后缀表达式中操作符应该出现在左括号对应的右括号位置,所以遇到左括号,要标记下来,其后出现的操作符的优先级提升了,一单扫描到对应的右括号,就可以马上输出这个操作符。
总结下,在从左到右扫描逐个字符扫描中缀表达式的过程中,采用一个栈来暂存未处理的操作符。这样,栈顶的操作符就是最近暂存进去的,当遇到一个新的操作符,就需要跟栈顶的操作符比较下优先级,再进行处理。
通用的中缀转后缀算法流程
在后面的算法描述中,约定中缀表达式是由空格隔开的一系列单词(token)构成,操作符单词包括* / + - (),而操作数单词则是单字母标识符A、B、C等。
首先,创建空栈s用于暂存操作符,空表li用于保存后缀表达式,将中缀表达式转换为单词列表,从左到右扫描中缀表达式单词列表。
如果单词是操作符,则直接添加到后缀表达式列表的末尾,如果单词是左括号“(”,则压入s栈顶,如果单词是右括号“)”,则反复弹出s栈顶,操作符加入到输出列表末尾,直到碰到左括号,如果单词是操作符“* / + -”,则压入s栈顶,但是在压入之前,要比较其与栈顶操作符的优先级。
中卓表示单词列表扫描结束后,把s栈中所有剩余操作符依次弹出,添加到输出列表末尾,把输出列表再用join方法合并成后缀表达式字符串,算法结束。
class Stack:
def __init__(self):
self.items = []
def isEmpty(self):
return self.items == []
def push(self, item):
return self.items.append(item)
def pop(self):
return self.items.pop()
def peek(self):
return self.items[len(self.items)-1]
def size(self):
return len(self.items)
def infixToPostfix(infixexpr):
# 记录操作符的优先级
p = {}
p["*"] = 2
p["/"] = 2
p["+"] = 1
p["-"] = 1
p["("] = 0
s = Stack() # 创建栈
li = [] # 用于保存后缀表达式列表
tokenList = infixexpr.split() # 将中缀表达式转换为单词列表
print(tokenList)
for token in tokenList:
if token in "ABCDEFGHIJKMNLOPQRSTUVWXWY" or token in "0123456789":
li.append(token)
elif token == "(":
s.push(token)
elif token == ")":
topToken = s.pop()
while topToken != "(":
li.append(topToken)
topToken = s.pop()
else:
while not s.isEmpty() and p[s.peek()] >= p[token]:
li.append(s.pop())
s.push(token)
while not s.isEmpty():
li.append(s.pop())
return " ".join(li)
后缀表达式求值
作为栈结构的结束,我们来讨论“后缀表达式求值”问题,跟中缀转换为后缀问题不同,在对后缀表达式从左到右扫描过程中,由于操作在操作数的后面,所以要暂存操作数,在碰到操作符的时候,再将暂存的两个操作数进行实际的计算,仍然是栈的特性:操作符只作用于离它最近的两个操作数。
如“4 5 6 * +”,我们先扫描到4,5两个操作数,但还不知道对这两个操作数能做什么计算,需要继续扫描后面的符号才能知道,继续扫描右碰到6,还是不知道如何计算,继续暂存入栈,直到“ * ”,现在知道是栈顶两个操作数5、6做乘法。
我们弹出两个操作数,计算得到结果为30,需要注意,先弹出的是右操作数,后弹出的是做操作数,这个对于-/很重要。
为了继续后续的计算,需要把这个中间结果30压入栈顶,继续扫描后面的符号,当所有操作符都处理完毕,栈中只留下一个操作数,就是表达式的值。
def postfixEval(postfixExpr):
s = Stack()
li = postfixExpr.split()
for l in li:
if l in "0123456789":
s.push(int(l))
else:
op2 = s.pop()
op1 = s.pop()
result = doMath(l, op1,op2)
s.push(result)
return s.pop()
def doMath(op, op1, op2):
if op == "*":
return op1 * op2
elif op == "/":
return op1 / op2
elif op == "+":
return op1 + op2
else:
return op1 -op2