斐波那契的四种求法

首先看一下斐波那契的矩阵表示：

数列的递推公式为：f(1)=1，f(2)=2，f(n)=f(n-1)+f(n-2)(n>=3)

　　 用矩阵表示为：

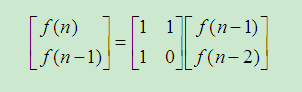
　　进一步，可以得出直接推导公式：

#include<iostream> 
#include<cstring>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<queue> 
#define N 1000
using namespace std;

int f[N]; 
int fibonacci_1(int n){//递归
    if(n==1 || n==0) return 1;
    return fibonacci_1(n-1) + fibonacci_1(n-2);
}

int fibonacci_2(int n){//递推
    f[0] = f[1] = 1;
    for(int i=2; i<=n; ++i)
        f[i] = f[i-1] + f[i-2];
    return f[n];
}

int fibonacci_3(int n){//非递归
    int f1=1, f2=1, f3;
    for(int i=2; i<=n; ++i){
        f3 = f1+f2;
        f2 = f1;
        f1 = f3;
    }
    return f1;
}

struct Fibonacci{
    int a11, a12, a21, a22;
    Fibonacci(){
    }
    Fibonacci(int a1, int a2, int a3, int a4){
        a11 = a1;
        a22 = a2;
        a21 = a3;
        a22 = a4;
    }
    Fibonacci operator *(Fibonacci x){
        Fibonacci* tmp = new Fibonacci();
        tmp->a11 = a11*x.a11 + a21*x.a21;
        tmp->a12 = a11*x.a12 + a21*x.a22;
        tmp->a21 = a21*x.a11 + a22*x.a21;
        tmp->a22 = a21*x.a21 + a22*x.a22;
        return *tmp;
    }
};

int fibonacci_4(int n){//矩阵 + 快速幂方法
    Fibonacci a(1, 1, 1, 0);
    Fibonacci ans(1, 0, 0, 1);
    while(n){//快速幂方法 
        if(n&1) ans = ans*a;
        a=a*a;
        n>>=1;
    }
    return ans.a11;
}
int main(){
    int n;
    cin>>n;
    cout<<"fibonacci_1: "<<fibonacci_1(n)<<endl;
    cout<<"fibonacci_2: "<<fibonacci_2(n)<<endl;
    cout<<"fibonacci_3: "<<fibonacci_3(n)<<endl;
    cout<<"fibonacci_4: "<<fibonacci_4(n)<<endl;
    return 0;
}