深度学习基础系列（六）| 权重初始化的选择

　　深层网络需要一个优良的权重初始化方案，目的是降低发生梯度爆炸和梯度消失的风险。先解释下梯度爆炸和梯度消失的原因，假设我们有如下前向传播路径：

　　a₁ = w₁x + b₁　　

　　z₁ = σ(a₁)

　　a₂ = w₂z₁ + b₂

　　z₂ = σ(a₂)

　　...

　　a_n = w_nz_n-1 + b_n

　　z_n = σ(a_n)

　　简化起见，令所有的b都为0，那么可得:

　　z_n =  σ(w_nσ(W_n-1σ(...σ(w₁x)))，

　　若进一步简化，令z = σ(a) = a，那么可得：

　　z_n = w_n * W_{n-1 *} W_n-1 *...* X

　　而权重w的选择，假定都为1.5，那么可观察到 z_n是呈现指数级递增，深层网络越深，意味着后面的值越大，呈现爆炸趋势；反之，w假定都为0.5，那么可观察到 z_n是呈现指数级递减，深层网络越深，意味着后面的值越小，呈现消失趋势。

　　若令z = σ(a) = sigmoid(a)，且a= ∑_nw_ix_i + b，其中n为输入参数的个数，当输入参数很多时，猜测|a|很大概率会大于1，对于sigmoid函数而言，|a|>1，则意味着曲线越来越平滑，z值会趋近于1或0，从而也会导致梯度消失。

　　那我们在每一层网络进行初始化权重时，若能给w一个合适的值，则能降低这种梯度爆炸或梯度消失的可能性吗？我们看看该如何选择。

一、随机分布权重

　　在keras中，其函数为：K.random_uniform_variable()，我们来直观地看看其数据分布图，先看代码：

import numpy as np
import matplotlib.pyplot as plt
import tensorflow.keras.backend as K

w = K.eval(K.random_uniform_variable(shape=(1, 10000), low=-1, high=1))
w = w.reshape(-1)
print("w:", w)

x = K.eval(K.random_uniform_variable(shape=(1, 10000), low=-1, high=1))
x = x.reshape(-1)
print("x:", x)

a = np.dot(w, x)
print("a:", a)

n, bins, patches = plt.hist(w, 50, density=1, facecolor='g', alpha=0.75)

plt.xlabel('data range')
plt.ylabel('probability')
plt.axis([-2, 2, 0, 1])
plt.grid(True)
plt.show()

　　其图像为：

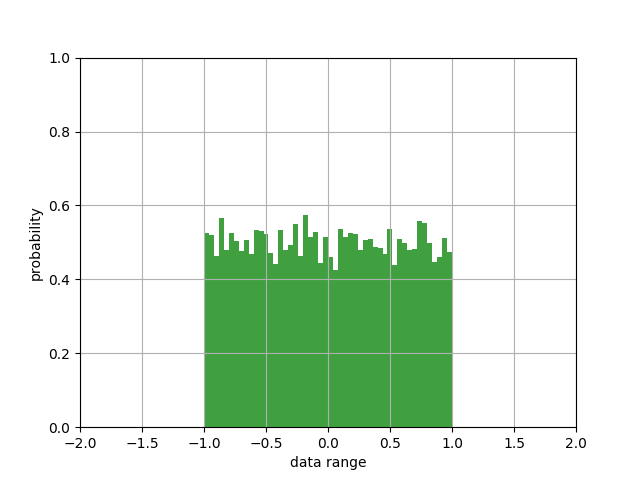
　　观察图像可知，随机函数取了10000个点，值范围被约束在-1~1之间，其概率分布都很均匀。

　　其输出结果为：

w: [-0.3033681   0.95340157  0.76744485 ...  0.24013376  0.5394962
 -0.23630977]
x: [-0.19380212  0.86640644  0.6185038  ... -0.66250014 -0.2095201
  0.23459053]
a: 16.111116

　　从结果可知，若我们的输入是10000个特征点，那么a= ∑₁₀₀₀₀w_ix_i + b，且|a|>1的概率很大（结果为16.111116）。可想而知，不采用激活函数或relu函数，则有梯度爆炸的可能性；若采用sigmoid激活函数的话，则会导致梯度消失。

二、正太分布权重

　　在keras中，其函数为：K.random_normal_variable()和K.truncated_normal()，我们来直观地看看其数据分布图，先看K.random_normal_variable代码：　

import numpy as np
import matplotlib.pyplot as plt
import tensorflow.keras.backend as K

w = K.eval(K.random_normal_variable(shape=(1, 10000), mean=0, scale=1))
w = w.reshape(-1)
print("w:", w)

x = K.eval(K.random_uniform_variable(shape=(1, 10000), low=-1, high=1))
x = x.reshape(-1)
print("x:", x)

a = np.dot(w, x)
print("a:", a)

n, bins, patches = plt.hist(w, 50, density=1, facecolor='g', alpha=0.75)

plt.xlabel('data range')
plt.ylabel('probability')
plt.axis([-5, 5, 0, 0.6])
plt.grid(True)
plt.show()

　　其图像为：

　　其结果为：

w: [-1.8685548   1.501203    1.1083876  ... -0.93544585  0.08100258
  0.4771947 ]
x: [ 0.40333223  0.7284522  -0.40256715 ...  0.79942155 -0.915035
  0.50783443]
a: -46.02679

　　再看看K.truncated_normal()的代码：

import numpy as np
import matplotlib.pyplot as plt
import tensorflow.keras.backend as K

w = K.eval(K.truncated_normal(shape=(1, 10000), mean=0, stddev=1))
w = w.reshape(-1)
print("w:", w)

x = K.eval(K.random_uniform_variable(shape=(1, 10000), low=-1, high=1))
x = x.reshape(-1)
print("x:", x)

a = np.dot(w, x)
print("a:", a)

n, bins, patches = plt.hist(w, 50, density=1, facecolor='g', alpha=0.75)

plt.xlabel('data range')
plt.ylabel('probability')
plt.axis([-5, 5, 0, 0.6])
plt.grid(True)
plt.show()

　　其图像为：

　

　　其结果为：

w: [ 1.0354282  -0.9385183   0.57337016 ... -0.3302136  -0.10443623
  0.9371711 ]
x: [-0.7896631  -0.01105547  0.778579   ...  0.7932384  -0.17074609
  0.60096693]
a: -18.191553

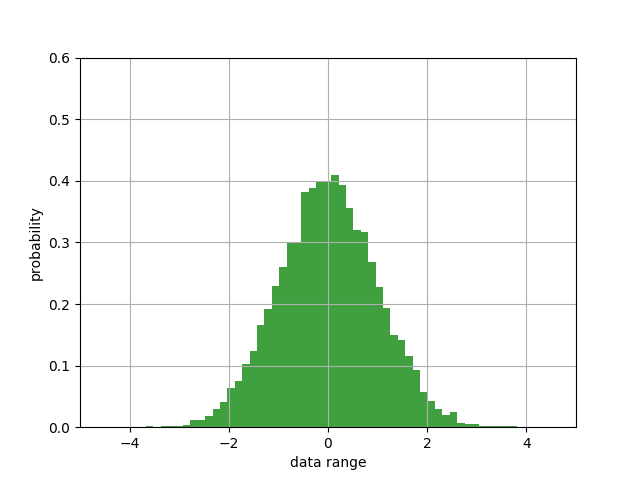
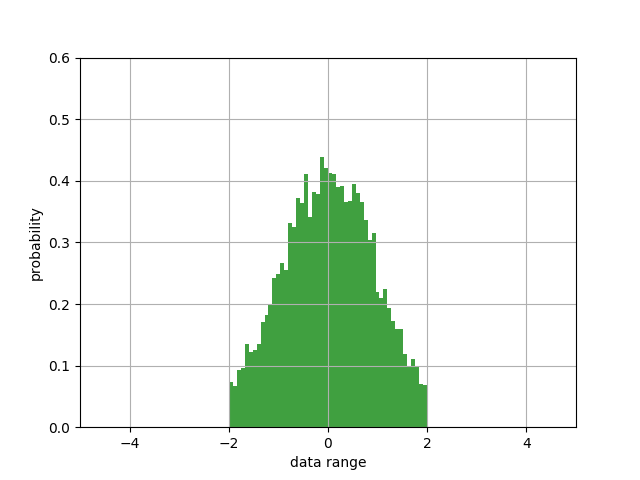
　　观察两个图像可知，两者都是正太分布图像，唯一区别在于K.truncated_normal()把大于2和小于2的数据给截断了，只保留了一部分数据。

　　从结果可知，若我们的输入是10000个特征点，那么a= ∑₁₀₀₀₀w_ix_i + b ，虽然图像具有一定的对称性，总体均值为0，但|a₁|>1依然有很大概率存在（结果为-18.191553），依旧有有梯度消失和爆炸的可能性。　　　　

三、正太收窄权重

　　我们的目标是使得|a₁| < 1，这样无论激活函数是sigmoid还是relu，都可以保证每一层的输出值不会增长太大，也不会增长过小。所以我们可以在正太分布的基础上，让其收窄变尖，可以让w_i=w_i / √n，其中n为该层的输入参数的数量，以10000个输出特征点为例，w_i=w_i / √10000，这样a₁= ∑₁₀₀₀₀w_ix_i + b₁ 就可以确保大致在-1~1范围内。可看代码：

import numpy as np
import matplotlib.pyplot as plt
import tensorflow.keras.backend as K

w = K.eval(K.random_normal_variable(shape=(1, 10000), mean=0, scale=1/np.sqrt(10000)))
w = w.reshape(-1)
print("w:", w)

x = K.eval(K.random_uniform_variable(shape=(1, 10000), low=-1, high=1))
x = x.reshape(-1)
print("x:", x)

a = np.dot(w, x)
print("a:", a)

n, bins, patches = plt.hist(w, 50, density=1, facecolor='g', alpha=0.75)

plt.xlabel('data range')
plt.ylabel('probability')
plt.axis([-0.1, 0.1, 0, 50])
plt.grid(True)
plt.show()

　　其图像为：

　　其结果为：

w: [ 0.00635913 -0.01406644 -0.00843588 ... -0.00573074  0.00345371
 -0.01102492]
x: [ 0.3738377  -0.01633143  0.21199775 ... -0.78332734 -0.96384525
 -0.3478613 ]
a: -0.4904538

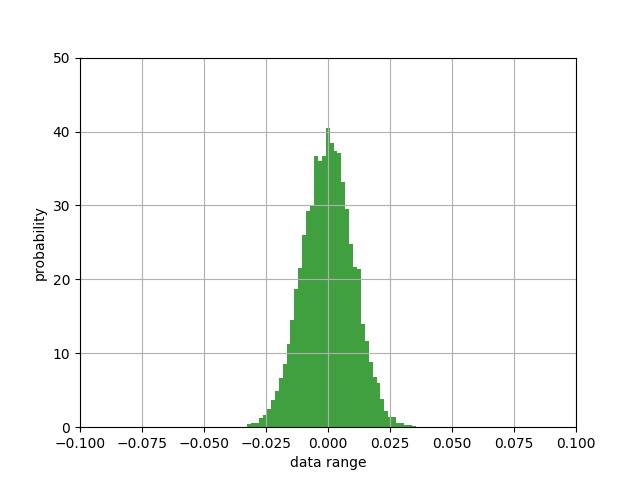
　　观察图像可知，数值范围已经被压缩在-0.025~0.025附近，概率值最高也到了40以上，变得又窄又尖了。

　　从结果也可知，我们成功地把|a|压缩在1范围以内，这个结果无论对sigmoid函数，还是relu函数，都是比较友好的，降低了梯度爆炸和梯度消失的风险，也利于加快训练学习过程。

四、Keras的默认选择

　　在使用Keras的Conv2D、Dense等函数时，会发现权重初始化的默认值为glorot_uniform，其对应网页为：https://www.tensorflow.org/api_docs/python/tf/glorot_uniform_initializer

　　可以看出glorot_uniform使用的是随机分布，不同之处在于其上下限值为[-limit, limit]，其中limit = sqrt(6 / (fan_in + fan_out))，fan_in即为输入特征数，而fa_out为输出特征数。其实和上述正太收紧类似，可以理解其数值范围是非常非常小。

　　在此不再赘述。