拓扑排序
1. 概念及规则
-
对一个有向无环图(
Directed Acyclic Graph简称DAG)G进行拓扑排序,是将G中所有顶点排成一个线性序列,使得图中任意一对顶点u和v,若边∈E(G),则u在线性序列中出现在v之前。通常,这样的线性序列称为满足拓扑次序(Topological Order)的序列,简称拓扑序列。简单的说,由某个集合上的一个偏序得到该集合上的一个全序,这个操作称之为拓扑排序。 -
规则:
-
图中每个顶点只出现一次。
-
A在B前面,则不存在B在A前面的路径。(否则就会形成环) -
顶点的顺序是
保证所有指向它的下个节点在被指节点前面
!
- 例如
A—>B—>C那么A一定在B前面,B一定在C前面。 - 这个核心规则下只要满足即可,所以拓扑排序序列不一定唯一!
- 例如
-
2. 算法及实现
-
Kahn算法-
实现步骤:
- 维护一个入度为
0的顶点的集合(栈、队列、优先队列皆可) - 每次从该集合中取出一个顶点
u(栈顶) - 遍历
u的邻接点v,v的入度rd[v]--,如果rd[v]==0,v进栈 - 队列为空,出栈数小于
n,存在环
- 维护一个入度为
-
时间复杂度:由于每个点入栈出栈一次,每条边扫描一次,时间复杂度为
O(n + e) -
图示:
-
删除
1或2以及对应边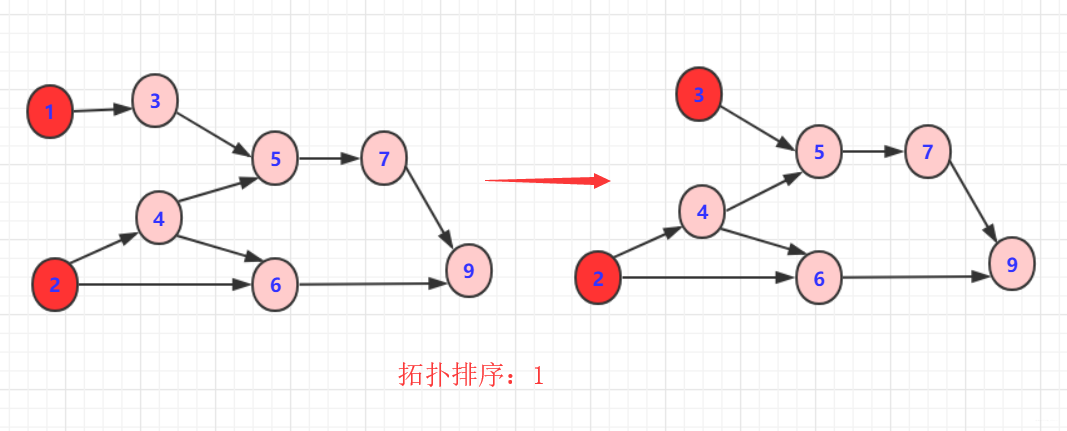
-
删除
2或3以及对应边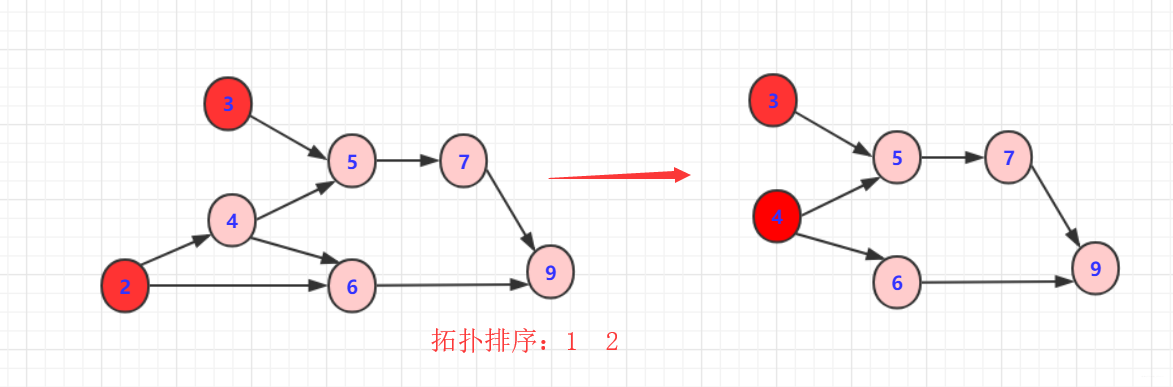
-
删除
3或者4以及对应边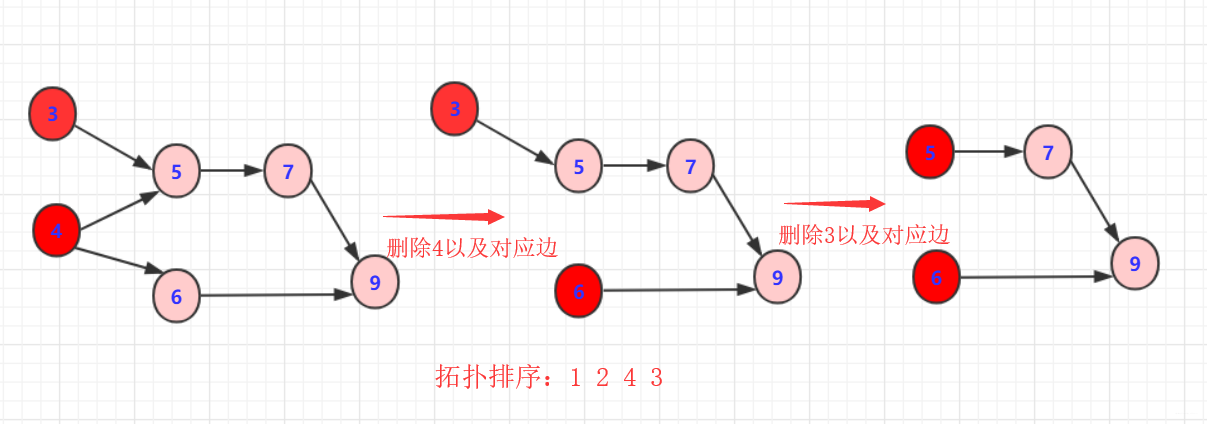
-
重复以上规则步骤
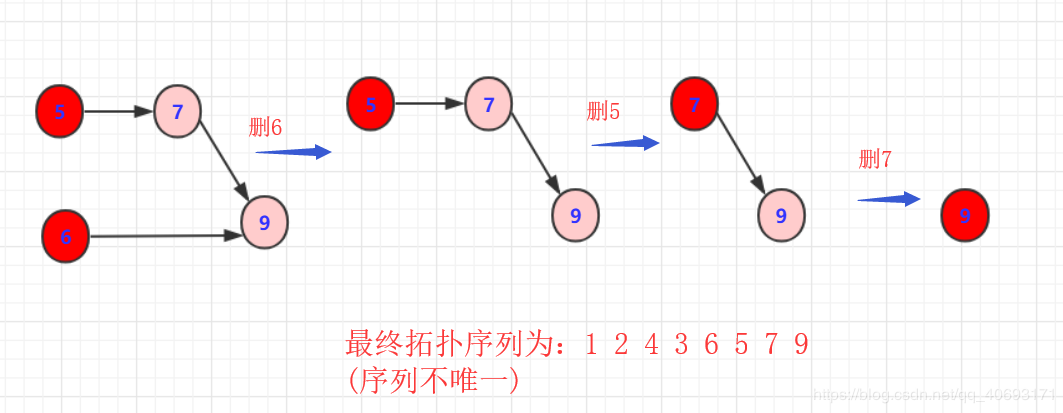
-
-
#include <bits/stdc++.h>
using namespace std;
csont int maxn = 10005;
struct edge{
int to, nx;
}e[maxn];
int n, m, len, head[maxn], rd[maxn], a[maxn];
void insert(int x, int y){//插边
e[++len].to = y;
e[len].nx = head[x];
head[x] = len;
}
void kahn(){
stact<int> stk;//维护入度为0的点
for(int i=1; i<n; i++) if(!rd[i]) stk.push(i);//如果入度为0,进栈
int cnt = 0;//记录出栈次数
while(!stk.empty()){
int u = stk.top();//获取栈顶
stk.pop();
a[++cnt] = u;//记录拓扑序
for(int i=head[u]; i; i=e[i].nx){//遍历邻接点
int v = e[i].to;
rd[v] --;//删边
if(!rd[v]) stk.push(v);//入度为0,进栈
}
}
if(cnt < n){printf("Cycle"); return;}//出栈次数小于n,有环
for(int i=1; i<=cnt; i++) printf("%d ", a[i]);
}
int main(){
scanf("%d%d", &n, &m);
for(int i=1; i<=m; i++){
int x, y; scanf("%d%d", &x, &y);
insert(x, y); rd[y] ++;
}
kahn();
return 0;
}