1、poj 3241 Object Clustering
题意:平面上有n个点,点之间的距离采用曼哈顿距离衡量。求一个最小距离X,使得在把这些点分为k组后,每组中两两点之间的距离不超过X。
思路:首先我们这么想,如果所有点都在1个组中,即k=1时,那么所要求的X即为该n个点的曼哈顿最小生成树的最大边;当k=2时,如果我们将最小生成树的最大边割开,形成2组,答案仍未原最小生成树的第2大的边(不会比之还小)……以此类推,可转换为求解平面上n个点的曼哈顿距离最小生成树的第k大的边的长度。
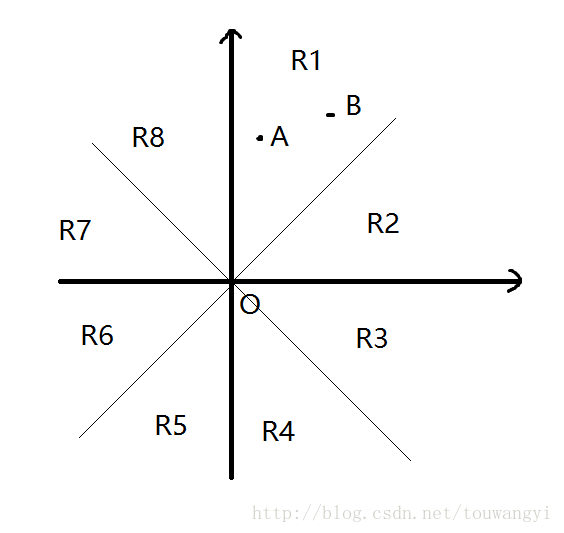
接下来,就是怎么构造曼哈顿最小生成树。如果我们将所有点两两建边再去寻找最小生成树,在n很大的情况下是不合适的,况且其中有一些边也没有必要建。我们把平面坐标分为8个区域:
 (转自:https://blog.csdn.net/touwangyi/article/details/77017360)
(转自:https://blog.csdn.net/touwangyi/article/details/77017360)
我们发现,根据对原点对称,我们分为四组:R1与R5,R2与R6,R3与R7,R4与R8。对于R1和R5内的点,假设当前点为O,我们在其位置上建立直角坐标系,那么对于其R1方向内的点A,B,我们没有必要连接O、B,只需连接O、A。因此,对于所有yi-yo>xi-xo,xi>xo即yi-xi>yo-xo,xi>xo的点i,找到最小的xi+yi那个点,将其与点O相连(记录下边)。这样,我们对点按照x为第一关键字升序、y为第二关键字升序,然后用树状数组维护区间最小值(xi+yi),用yi-xi离散化后的编号作为树状数组的下标,从最后一个点起更新树状数组。
对于其余区域,我们计算完R1与R5后,先让所有点关于y=x对称,则R2、R6内的点转到R1、R5区域,用对待原R1、R5内的点同样对待它们。因此,类似地,我们通过3次旋转、4次更新树状数组和连边,就得到所有有效的边,接下来,利用最小生成树原理,找到第n-1-(k-1)次添加进生成树的边的边权即可。

1 #include<iostream> 2 #include<vector> 3 #include<algorithm> 4 using namespace std; 5 const int maxn = 1e5 + 10; 6 const int INF = 0x3f3f3f3f; 7 int n,k; 8 /*树状数组维护最小值*/ 9 struct node1 10 { 11 int val, id;//val表示ai+bi,id表示对应的点 12 }tree[maxn]; 13 void tree_init() 14 { 15 for (int i = 0; i < maxn; i++) tree[i].val = INF, tree[i].id = -1; 16 } 17 int lowbit(int x) 18 { 19 return x & (-x); 20 } 21 void update(int x, int val, int id) 22 { 23 while (x) 24 { 25 if (tree[x].val > val) tree[x].val = val, tree[x].id = id; 26 x -= lowbit(x); 27 } 28 } 29 int query(int x, int MAX) 30 { 31 int minv = INF, ans = -1; 32 while (x <= MAX) 33 { 34 if (tree[x].val < minv) minv = tree[x].val, ans = tree[x].id; 35 x += lowbit(x); 36 } 37 return ans; 38 } 39 /*树状数组结束*/ 40 struct P 41 { 42 int ai, bi,id; 43 friend bool operator<(const P&p1, const P&p2) 44 { 45 if (p1.ai == p2.ai) return p1.bi < p2.bi; 46 else return p1.ai < p2.ai; 47 } 48 }points[maxn]; 49 struct EDGE 50 { 51 int from, to, dist; 52 EDGE(int ff=0,int uu=0,int dd=0):from(ff),to(uu),dist(dd){} 53 friend bool operator<(const EDGE&e1, const EDGE&e2) 54 { 55 return e1.dist < e2.dist; 56 } 57 }edge[maxn<<1]; 58 int totedge; 59 void addedge(int u, int v,int id1,int id2) 60 { 61 edge[totedge] = EDGE(u, v, abs(points[id1].ai-points[id2].ai)+abs(points[id1].bi-points[id2].bi)); 62 totedge++; 63 } 64 int v1[maxn];//bi-ai 65 vector<int>all; 66 int sz; 67 int get_id(int v) 68 { 69 return lower_bound(all.begin(), all.end(), v) - all.begin()+1; 70 } 71 void R1_addedge() 72 {//对R1、R5内点建边 73 sort(points + 1, points + 1 + n); 74 all.clear(); 75 for (int i = 1; i <= n; i++) v1[i] = points[i].bi - points[i].ai, all.push_back(v1[i]); 76 sort(all.begin(), all.end()); 77 all.erase(unique(all.begin(), all.end()), all.end()); 78 sz = all.size(); 79 tree_init(); 80 for (int i = n; i >= 1; --i) 81 { 82 int pos = get_id(v1[i]); 83 int tans = query(pos, sz); 84 if (tans != -1) 85 { 86 addedge(points[i].id, points[tans].id, i, tans); 87 } 88 update(pos, points[i].ai + points[i].bi, i); 89 } 90 } 91 /*并查集*/ 92 int pre[maxn]; 93 int Find(int x) 94 { 95 if (pre[x] == x) return x; 96 else 97 { 98 int fa = pre[x]; 99 pre[x] = Find(fa); 100 return pre[x]; 101 } 102 } 103 /* 104 连好R1域后,把所有点按直线y = x翻转(此时初始的R2域的到了R1域,初始的R3域的到了R8域,初始的R4域的到了R7域),就可以求R2域了;再把所有点按直线x = 0翻转(此时初始的R3域(之前在R8域)的到了R1域,初始的R4域(之前在R7)的到了R2域),就可以求R3域了;再把所有点按直线y = x翻转(此时初始的R4域(之前在R2域)的到了R1域,就可以求R4域 105 */ 106 void ManHattan_addedge() 107 { 108 for (int dir = 0; dir < 4; dir++) 109 { 110 if (dir == 1 || dir == 3) 111 { 112 for (int i = 1; i <= n; i++) swap(points[i].ai, points[i].bi); 113 } 114 else if (dir == 2) 115 { 116 for (int i = 1; i <= n; i++) points[i].ai = -points[i].ai; 117 } 118 R1_addedge(); 119 } 120 } 121 int k_ans; 122 void solve() 123 { 124 for (int i = 0; i <= n; i++) pre[i] = i; 125 sort(edge, edge + totedge); 126 int cur = 0, remain = n - 1,now=0; 127 while (remain&&now<totedge) 128 { 129 int u = edge[now].from, v = edge[now].to; 130 int fu = Find(u), fv = Find(v); 131 if (fu != fv) 132 { 133 remain--, cur++; 134 if (remain == k - 1) 135 { 136 k_ans = edge[now].dist; 137 return; 138 } 139 pre[fu] = fv; 140 } 141 now++; 142 } 143 } 144 int main() 145 { 146 while (~scanf("%d%d", &n, &k) && n) 147 { 148 totedge = 0; 149 for (int i = 1; i <= n; i++) scanf("%d%d", &points[i].ai, &points[i].bi), points[i].id = i; 150 ManHattan_addedge(); 151 solve(); 152 printf("%d ", k_ans); 153 } 154 155 return 0; 156 }
2、Another Minimum Spanning Tree UVALive - 3662
题意:给出平面图上n个点,求这些点形成的曼哈顿最小生成树的总权值。
思路:曼哈顿最小生成树模板题。

1 #include<iostream> 2 #include<vector> 3 #include<algorithm> 4 using namespace std; 5 const int maxn = 1e5 + 10; 6 const int INF = 0x3f3f3f3f; 7 int n; 8 long long ret; 9 /*树状数组维护最小值*/ 10 struct node1 11 { 12 int val, id;//val表示ai+bi,id表示对应的点 13 }tree[maxn]; 14 void tree_init() 15 { 16 for (int i = 0; i < maxn; i++) tree[i].val = INF, tree[i].id = -1; 17 } 18 int lowbit(int x) 19 { 20 return x & (-x); 21 } 22 void update(int x, int val, int id) 23 { 24 while (x) 25 { 26 if (tree[x].val > val) tree[x].val = val, tree[x].id = id; 27 x -= lowbit(x); 28 } 29 } 30 int query(int x, int MAX) 31 { 32 int minv = INF, ans = -1; 33 while (x <= MAX) 34 { 35 if (tree[x].val < minv) minv = tree[x].val, ans = tree[x].id; 36 x += lowbit(x); 37 } 38 return ans; 39 } 40 /*树状数组结束*/ 41 struct P 42 { 43 int ai, bi,id; 44 friend bool operator<(const P&p1, const P&p2) 45 { 46 if (p1.ai == p2.ai) return p1.bi < p2.bi; 47 else return p1.ai < p2.ai; 48 } 49 }points[maxn]; 50 struct EDGE 51 { 52 int from, to, dist; 53 EDGE(int ff=0,int uu=0,int dd=0):from(ff),to(uu),dist(dd){} 54 friend bool operator<(const EDGE&e1, const EDGE&e2) 55 { 56 return e1.dist < e2.dist; 57 } 58 }edge[maxn*10]; 59 int totedge; 60 int cal_dis(int p1,int p2) 61 { 62 return abs(points[p1].ai-points[p2].ai)+abs(points[p1].bi-points[p2].bi); 63 } 64 void addedge(int u, int v,int id1,int id2) 65 { 66 edge[totedge] = EDGE(u, v,cal_dis(id1,id2)); 67 totedge++; 68 } 69 int v1[maxn];//bi-ai 70 vector<int>all; 71 int sz; 72 int get_id(int v) 73 { 74 return lower_bound(all.begin(), all.end(), v) - all.begin()+1; 75 } 76 void R1_addedge() 77 {//对R1、R5内点建边 78 sort(points + 1, points + 1 + n); 79 all.clear(); 80 for (int i = 1; i <= n; i++) v1[i] = points[i].bi - points[i].ai, all.push_back(v1[i]); 81 sort(all.begin(), all.end()); 82 all.erase(unique(all.begin(), all.end()), all.end()); 83 sz = all.size(); 84 tree_init(); 85 for (int i = n; i >= 1; --i) 86 { 87 int pos = get_id(v1[i]); 88 int tans = query(pos, sz); 89 if (tans != -1) 90 { 91 addedge(points[i].id, points[tans].id, i, tans); 92 } 93 update(pos, points[i].ai + points[i].bi, i); 94 } 95 } 96 /* 97 连好R1域后,把所有点按直线y = x翻转(此时初始的R2域的到了R1域,初始的R3域的到了R8域,初始的R4域的到了R7域), 98 就可以求R2域了;再把所有点按直线x = 0翻转(此时初始的R3域(之前在R8域)的到了R1域,初始的R4域(之前在R7)的到了R2域) 99 ,就可以求R3域了;再把所有点按直线y = x翻转(此时初始的R4域(之前在R2域)的到了R1域,就可以求R4域 100 */ 101 void ManHattan_addedge() 102 { 103 for (int dir = 0; dir < 4; dir++) 104 { 105 if (dir == 1 || dir == 3) 106 { 107 for (int i = 1; i <= n; i++) swap(points[i].ai, points[i].bi); 108 } 109 else if (dir == 2) 110 { 111 for (int i = 1; i <= n; i++) points[i].ai = -points[i].ai; 112 } 113 R1_addedge(); 114 } 115 } 116 /*并查集*/ 117 int pre[maxn]; 118 int Find(int x) 119 { 120 if (pre[x] == x) return x; 121 else 122 { 123 int fa = pre[x]; 124 pre[x] = Find(fa); 125 return pre[x]; 126 } 127 } 128 void solve() 129 { 130 for (int i = 0; i <= n; i++) pre[i] = i; 131 ret=0; 132 sort(edge, edge + totedge); 133 int remain = n - 1,now=0; 134 while (remain&&now<totedge) 135 { 136 int u = edge[now].from, v = edge[now].to; 137 int fu = Find(u), fv = Find(v); 138 if (fu != fv) 139 { 140 remain--; 141 pre[fu] = fv; 142 ret+=edge[now].dist; 143 } 144 now++; 145 } 146 } 147 int main() 148 { 149 int Case=1; 150 while (~scanf("%d", &n) && n) 151 { 152 totedge = 0; 153 for (int i = 1; i <= n; i++) scanf("%d%d", &points[i].ai, &points[i].bi), points[i].id = i; 154 ManHattan_addedge(); 155 solve(); 156 printf("Case %d: Total Weight = %lld ",Case++,ret); 157 } 158 159 return 0; 160 }
