第二章
2.12
(1)拟合模型:
> library(openxlsx) #加载包 openxlsx
> data = read.xlsx("22_data.xlsx",sheet = 2) #read.xlsx 函数读入数据
> x = data[,1]
> y = data[,2]
> res = lm(y~x) #构造线性回归模型函数
> res #结果
Call:
lm(formula = y ~ x)
Coefficients:
(Intercept) x #得出线性回归模型 y = -6.332 + 9.208 x
-6.332 9.208
> summary(res) #打印方差分析,系数的估计值及其检验。
Call:
lm(formula = y ~ x)
Residuals: #残差统计量,残差第一四分位数(1Q)和第三分位数(3Q)有大约相同的幅度,意味着有较对称的钟形分布
Min 1Q Median 3Q Max
-2.5629 -1.2581 -0.2550 0.8681 4.0581
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -6.33209 1.67005 -3.792 0.00353 ** #截距的点估计值及其检验
x 9.20847 0.03382 272.255 < 2e-16 *** #自变量系数的点估计值及其检验
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1.946 on 10 degrees of freedom
Multiple R-squared: 0.9999, Adjusted R-squared: 0.9999 #相关系数与调整的相关系数
F-statistic: 7.412e+04 on 1 and 10 DF, p-value: < 2.2e-16 #模型的显著性检验(F检验)
(2)根据上面程序结果,自变量具有显著性,模型具有显著性。
(3) 不能支持管理员的观点,根据构造的线性回归模型,平均环境温度增加1°F,平均月水蒸气消耗量将增加 9208+lb ,达不到10000lb.
(4) 使用58°F的平均环境温度构造一个月中水蒸气消耗量的99%预测区间:
> library(openxlsx)
> data = read.xlsx("22_data.xlsx",sheet = 2)
> x = data[,1]
> y = data[,2]
> fun = function(x) #计算预测值函数
+ {
+ y = -6.332 + 9.208*x
+ }
> y_pred = fun(x) #计算所有数的预测值
> s_y0_pred = function(x0,x,y,n) #构造计算预测值标准差的函数
+ {
+ n = 12
+ y_pred = fun(x)
+ sse = sum((y_pred - y)*(y_pred - y))
+ se = sqrt(sse/(n-2))
+ se * sqrt(1/n + ((x0-mean(x))^2)/sum((x-rep(mean(x),n))^2))
+ }
> x0 = 58 ; n = 12
> y0_pred = fun(x0) #当环境温度为58°F,对应的因变量预测值
> s = s_y0_pred(x0,x,y,n)
> print(c(y0_pred-qt(0.995,n-2)*s,y0_pred+qt(0.995,n-2)*s)) #输出结果
[1] 525.5666 529.8974
2.13
a.做出散点图
> data = read.xlsx("22_data.xlsx",sheet = 1)
> x = data[,2]
> y = data[,1]
> plot(x,y,main = "散点图",xlab = "index",ylab = "days")
> abline(lm(y~x))
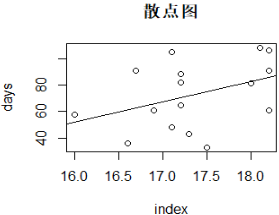
b.估计预测方程
> lm(y~x)
Call:
lm(formula = y ~ x)
Coefficients:
(Intercept) x
-193.0 15.3
预测方程为:y = *-193.0 + 15.3 x
c.进行回归显著性检验
> summary(lm(y~x))
Call:
lm(formula = y ~ x)
Residuals:
Min 1Q Median 3Q Max
-41.70 -21.54 2.12 18.56 36.42
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -192.984 163.503 -1.180 0.258 #p值大于0.05
x 15.296 9.421 1.624 0.127 #p值大于0.05 , 回归变量与响应变量没有显著相关性
Residual standard error: 23.79 on 14 degrees of freedom
Multiple R-squared: 0.1585, Adjusted R-squared: 0.09835
F-statistic: 2.636 on 1 and 14 DF, p-value: 0.1267
根据上述结果,指数与天数并没有显著相关性。
d.计算并画出95%置信带与95%预测带
> sx = sort(x)
> #计算置信区间 > conf = predict(fm,data.frame(x = sx),interval = "confidence") > #计算预测区间 > pred = predict(fm,data.frame(x=sx),interval = "prediction") > plot(x,y,ylim = c(0,150),xlab = "index",ylab = "days",main = "95%预测带、置信带") > abline(fm) > lines(sx,conf[,2],col = "red") > lines(sx,conf[,3],col = "red") > lines(sx,pred[,2],col = "blue") > lines(sx,pred[,3],col = "blue")
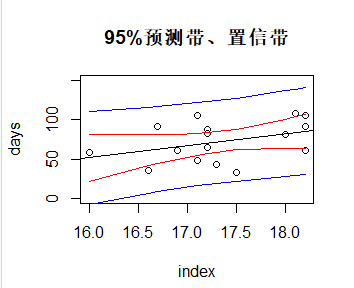
2.14
a.散点图

b.估计预测方程
> fm = lm(y~x)
> fm
Call:
lm(formula = y ~ x)
Coefficients:
(Intercept) x
0.6714 -0.2964
预测方程为:y = 0.6714 - 0.2964 x
c.数据分析
> summary(fm)
Call:
lm(formula = y ~ x)
Residuals:
Min 1Q Median 3Q Max
-0.20464 -0.10634 0.02196 0.08527 0.20643
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.6714 0.1595 4.209 0.00563 **
x -0.2964 0.2314 -1.281 0.24754 #p值大于0.05 ,该自变量没有显著相关
---
Signif. codes:
0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.15 on 6 degrees of freedom
Multiple R-squared: 0.2147, Adjusted R-squared: 0.08382 R^2 = 0.2147
F-statistic: 1.64 on 1 and 6 DF, p-value: 0.2475 #整个模型不具有显著性。
d.计算并画出95%置信带和95%预测带
> plot(x,y,main = "散点图",xlab = "比率",ylab = "黏度",ylim = c(-0.1,1)) > sx = sort(x) > conf = predict(fm,data.frame(sx),interval = "confidence") > pred = predict(fm,data.frame(sx),interval = "prediction") > abline(fm) > lines(sx,conf[,2],col = "red") #绘制置信下限 > lines(sx,conf[,3],col = "red") #绘制置信上限 > lines(sx,pred[,2],col = "blue") #绘制预测下限 > lines(sx,pred[,3],col = "blue") #绘制预测上限

2.15
a.估计预测方程
Call: lm(formula = y ~ x) Coefficients: (Intercept) x 1.281511 -0.008758
预测方程为: y = 1.281511 - 0.008758 x
b.全面分析此模型
> fm = lm(y~x)
> summary(fm)
Call:
lm(formula = y ~ x)
Residuals:
Min 1Q Median 3Q Max
-0.043955 -0.035863 -0.009305 0.019900 0.069559
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.2815107 0.0468683 27.34 1.58e-07 ***
x -0.0087578 0.0007284 -12.02 2.01e-05 *** #根据 p 值,自变量温度极显著
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.04743 on 6 degrees of freedom
Multiple R-squared: 0.9602, Adjusted R-squared: 0.9535
F-statistic: 144.6 on 1 and 6 DF, p-value: 2.007e-05 #根据 p 值,整个回归模型是显著的
c.画95%置信带、预测带
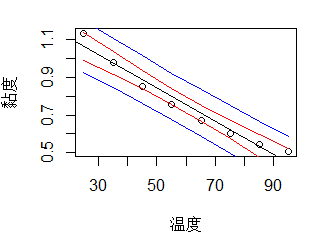
2.16
先画出散点图:
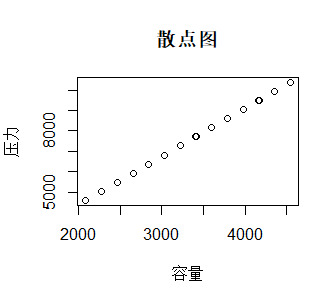
从散点图可以看出容量与压力之间具有明显的线性关系,我们构造一元线性模型:
> fm = lm(y~x) > fm Call: lm(formula = y ~ x) Coefficients: (Intercept) x -290.707 2.346
估计预测模型为: y = -290.707 + 2.346x
再对模型进行检验:
> summary(fm)
Call:
lm(formula = y ~ x)
Residuals:
Min 1Q Median 3Q Max
-4.3276 -0.9227 0.0773 1.2676 2.9577
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -2.907e+02 1.355e+00 -214.6 <2e-16 ***
x 2.346e+00 4.007e-04 5855.4 <2e-16 *** #该自变量极显著
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1.741 on 31 degrees of freedom
Multiple R-squared: 1, Adjusted R-squared: 1
F-statistic: 3.429e+07 on 1 and 31 DF, p-value: < 2.2e-16 #整个回归模型极显著
2.17
> x = data[,2]
> y = data[,1]
> n = length(x)
> plot(x,y)
>
> fm = lm(y~x) #一元回归模型
> abline(fm)
> coef(fm)
(Intercept) x
163.930734 1.579647
> summary(fm)
Call:
lm(formula = y ~ x)
Residuals:
Min 1Q Median 3Q Max
-1.41483 -0.91550 -0.05148 0.76941 2.72840
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 163.9307 2.6551 61.74 < 2e-16 ***
x 1.5796 0.1051 15.04 1.88e-10 ***
---
Signif. codes:
0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1.291 on 15 degrees of freedom
Multiple R-squared: 0.9378, Adjusted R-squared: 0.9336
F-statistic: 226 on 1 and 15 DF, p-value: 1.879e-10
> anova(fm) #方差分析
Analysis of Variance Table
Response: y
Df Sum Sq Mean Sq F value Pr(>F)
x 1 376.92 376.92 226.04 1.879e-10 ***
Residuals 15 25.01 1.67
---
Signif. codes:
0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
>
> rm(list = ls())
2.18
library(openxlsx)
data = read.xlsx("2.18.xlsx",sheet = 1)
x = data[,2]
y = data[,3]
n = length(x)
plot(x,y)
fm = lm(y~x) #一元回归
coef(fm) #输出回归系数
summary(fm)
anova(fm)
#构造此数据的95%置信带与预测带
sx = sort(x)
conf = predict(fm,data.frame(x = sx),interval = "confidence")
pred = predict(fm,data.frame(x = sx),interval = "prediction")
abline(fm)
lines(sx,conf[,2],col = 'red')
lines(sx,conf[,3],col = 'red')
lines(sx,pred[,2],col = 'blue')
lines(sx,pred[,3],col = 'blue')
plot(x,y,main = "%95置信带与95%预测带",xlab = "花费钱数",ylab = "每周挣回的印象",ylim=c(-100,200))
rm(list = ls())
第三章
3.8
#a.拟合co2产量y与总溶剂量x6和氢消耗量x7关系的多元回归模型
library(openxlsx) data = read.xlsx("3.8.xlsx",sheet = 1) data y = data[,1] #响应变量 x = data[,c(7,8)] #回归变量 fm = lm(y~.,x) #多元线性回归 summary(fm) anova(fm) #检验显著性 summary(fm) #d confint(fm) #e x6 = data[,7] fm1 = lm(y~x6) summary(fm1) anova(fm1) confint(fm1,level = 0.95) rm(list = ls())
3.9
library(openxlsx)
data = read.xlsx("3.9.xlsx",sheet = 1)
y = data[,1]
x = data[,c(2,5)]
#a.拟合多元回归模型
fm = lm(y~.,x)
coef(fm)
#b,c 检验回归显著性()
anova(fm)
summary(fm)
#e
#检验是否有潜在的多重共线性
r2 = 0.6367
vif = 1/(1-r2)
rm(list = ls())
3.10
> #3.10
> library(openxlsx)
> data = read.xlsx("3.10.xlsx",sheet = 1)
> #a
> y = data[,6]
> x = data[,c(1:5)]
> fm = lm(y~.,x)
> coef(fm)
(Intercept) Clarity Aroma Body Flavor
3.9968648 2.3394535 0.4825505 0.2731612 1.1683238
Oakiness
-0.6840102
> #b,c
> summary(fm)
Call:
lm(formula = y ~ ., data = x)
Residuals:
Min 1Q Median 3Q Max
-2.85552 -0.57448 -0.07092 0.67275 1.68093
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.9969 2.2318 1.791 0.082775 .
Clarity 2.3395 1.7348 1.349 0.186958
Aroma 0.4826 0.2724 1.771 0.086058 .
Body 0.2732 0.3326 0.821 0.417503
Flavor 1.1683 0.3045 3.837 0.000552 ***
Oakiness -0.6840 0.2712 -2.522 0.016833 *
---
Signif. codes:
0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1.163 on 32 degrees of freedom
Multiple R-squared: 0.7206, Adjusted R-squared: 0.6769
F-statistic: 16.51 on 5 and 32 DF, p-value: 4.703e-08
> #d
> xx = data[,c(2,4)]
> fm1 = lm(y~.,xx)
> summary(fm1)
Call:
lm(formula = y ~ ., data = xx)
Residuals:
Min 1Q Median 3Q Max
-2.19048 -0.60300 -0.03203 0.66039 2.46287
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 4.3462 1.0091 4.307 0.000127 ***
Aroma 0.5180 0.2759 1.877 0.068849 .
Flavor 1.1702 0.2905 4.027 0.000288 ***
---
Signif. codes:
0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1.229 on 35 degrees of freedom
Multiple R-squared: 0.6586, Adjusted R-squared: 0.639
F-statistic: 33.75 on 2 and 35 DF, p-value: 6.811e-09
> AIC(fm) #优先考虑的模型应是AIC值最小的那一个
[1] 126.7552
> AIC(fm1)
[1] 128.3761
> #e
> conf = confint(fm)
> conf1 = confint(fm1)
> conf = as.matrix(conf)
> conf1 = as.matrix(conf1)
>
> conf[5,2]-conf[5,1]
[1] 1.240414
> conf1[3,2]-conf[3,1]
[1] 1.83241
>
> rm(list = ls())
>
3.11
> #3.11
> library(openxlsx)
> data = read.xlsx("3.11.xlsx",sheet = 1)
> y = data[,6]
> x = data[,c(1:5)]
> #a
> fm = lm(y~.,x)
> coef(fm)
(Intercept) x1 x2 x3
5.207905e+01 5.555556e-02 2.821429e-01 1.250000e-01
x4 x5
1.776357e-16 -1.606498e+01
> #b,c
> summary(fm)
Call:
lm(formula = y ~ ., data = x)
Residuals:
Min 1Q Median 3Q Max
-12.250 -4.438 0.125 5.250 9.500
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 5.208e+01 1.889e+01 2.757 0.020218 *
x1 5.556e-02 2.987e-02 1.860 0.092544 .
x2 2.821e-01 5.761e-02 4.897 0.000625 ***
x3 1.250e-01 4.033e-01 0.310 0.762949
x4 1.776e-16 2.016e-01 0.000 1.000000
x5 -1.606e+01 1.456e+00 -11.035 6.4e-07 ***
---
Signif. codes:
0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 8.065 on 10 degrees of freedom
Multiple R-squared: 0.9372, Adjusted R-squared: 0.9058
F-statistic: 29.86 on 5 and 10 DF, p-value: 1.055e-05
> #d
> xx = data[,c(2,5)]
> fm1 = lm(y~.,xx)
> summary(fm1)
Call:
lm(formula = y ~ ., data = xx)
Residuals:
Min 1Q Median 3Q Max
-15.375 -4.188 -0.875 3.438 12.625
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 80.13461 5.69146 14.080 3.01e-09 ***
x2 0.28214 0.05883 4.796 0.000349 ***
x5 -16.06498 1.48659 -10.807 7.26e-08 ***
---
Signif. codes:
0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 8.236 on 13 degrees of freedom
Multiple R-squared: 0.9149, Adjusted R-squared: 0.9018
F-statistic: 69.89 on 2 and 13 DF, p-value: 1.107e-07
> AIC(fm)
[1] 118.6885
> AIC(fm1)
[1] 117.5552
>
> #e
> confint(fm)
2.5 % 97.5 %
(Intercept) 9.99688896 94.1612109
x1 -0.01100273 0.1221138
x2 0.15378045 0.4105053
x3 -0.77353688 1.0235369
x4 -0.44926844 0.4492684
x5 -19.30879739 -12.8211665
> confint(fm1) #温度:x2
2.5 % 97.5 %
(Intercept) 67.8389462 92.4302647
x2 0.1550559 0.4092298
x5 -19.2765650 -12.8533989
>
第四章
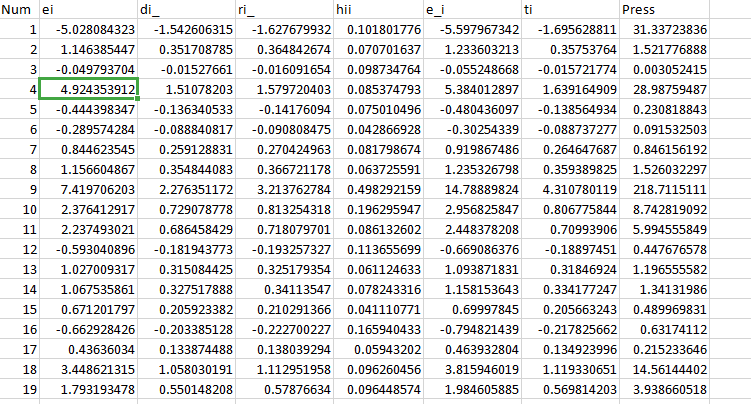
例4.1 根据例3.1数据,输出残差,标准化残差,学生化残差,press残差,外部学生化残差 表格
library(openxlsx)
#例4.1---------------------------------------------------------
#处理数据
data = read.xlsx("3.1.xlsx",sheet = 1)
data = data[,c(2,3,4)]
names(data)=c("time","cases","distance")
y = data$time
x1 = data$cases
x2 = data$distance
#线性回归
fm = lm(y~x1+x2)
#残差
ei = residuals(fm)
View(ei)
#标准化残差(1)
di = rstandard(fm)
View(di)
#计算mse的函数
mse = function(ei,p) #ei是残差向量,p是回归参数个数
{
n = length(ei)
sse = sum(ei**2)
mse = sse/(n-p)
return(mse)
}
di_ = ei/sqrt(mse(ei,3))#标准化残差(2)
View(di_)
#学生化残差(1)
ri = rstudent(fm)
View(ri)
#计算帽子矩阵,并提取对角线元素
H = function(X) #X是回归向量矩阵
{
h = X%*%solve(t(X)%*%X)%*%t(X)
hii = diag(h)
return(hii)
}
X = cbind(1,x1,x2)
hii = H(X) #计算hii
View(hii)
ri_ = ei/sqrt(mse(ei,3)*(1-hii)) #学生化残差(2)
View(ri_)
#计算PRESS统计量
e_i = ei/(1-hii) #计算e(i)
View(e_i)
#外部学生化残差
ti = function(ei,X) #输入残差回归变量矩阵
{
p = ncol(X) #回归参数个数
n = length(ei) #数据个数
hii = H(X) #帽子矩阵主对角线元素
s2_i = ((n-p)*mse(ei,p) -(ei**2)/(1-hii)) / (n-p-1) #计算S(i)^2
ans = ei / sqrt(s2_i*(1-hii))
return(ans)
}
ti = ti(ei,X)
View(ti)
#计算PRESS统计量
press = function(ei,X)
{
hii = H(X)
res = sum((ei/(1-hii))**2)
#View(res)
}
Press = (ei/(1-hii))**2
View(Press)
PRESS = press(ei,X) #输出PRESS统计量
#将所有残差数据写入表格
Num = seq(1,length(ei))
mydata = cbind(Num,ei,di_,ri_,hii,e_i,ti,Press)
class(mydata)
View(mydata)
write.xlsx(mydata,"C:\Users\86130\Desktop\mydata.xlsx")
#例4.2
ti #外部学生化残差
View(ti)
n = length(ti) #数据个数
order = rank(ti) #rank函数返回ti按升序排序之后的序号
Pi = (order-1/2)/n #累积概率
plot(ti,Pi,xlim=c(-3,5)) #画正态概率图
fm_tP = lm(Pi~ti) #线性回归模型
abline(fm_tP) #添加回归线
#例4.3
#画残差与拟合值y_i的残差图
plot(fitted(fm),ti) #fitted(fm)返回模型fm的预测值
abline(h = 0) #添加直线y=0
#例4.4
#画残差与回归变量的残差图
par(mfrow =c(1,2))
plot(x1,ti,xlab = "箱数",ylab = "外部学生化残差")
abline(h=0) #h:y轴 v:x轴
plot(x2,ti,xlab = "距离",ylab = "外部学生化残差")
abline(h=0)
#例4.5
#画偏回归图
#回归变量x1的偏回归图
lm.y_x2 = lm(y~x2)
lm.x1_x2 = lm(x1~x2)
plot(resid(lm.x1_x2),resid(lm.y_x2),xlab = "箱数",ylab = "时间")
#回归变量x2的偏回归图
lm.y_x1 = lm(y~x1)
lm.x2_x1 = lm(x2~x1)
plot(resid(lm.x2_x1),resid(lm.y_x1),xlab = "距离",ylab = "时间",pch = 10)
#例4.6
#计算PRESS的预测R^2
R_pred = function(X,y)
{
hii = H(X)
ei = resid(lm(y~X[,2]+X[,3]))
PRESS = sum((ei/(1-hii))**2)
sst = sum((y-mean(y))**2)
ans = 1-PRESS/sst
return(ans)
}
R_pred(X,y)
#例4.7
data = read.xlsx("2.1.xlsx",sheet = 1)
names(data) = c("order","y","x")
x = data$x
y = data$y
X = cbind(1,x)
fm = lm(y~x)
#绘制正态概率图
plot_ZP = function(ti) #输入外部学生化残差
{
n = length(ti)
order = rank(ti) #按升序排列,t(i)是第order个
Pi = (order-1/2)/n #累积概率
plot(ti,Pi,xlim=c(-3,3),xlab = "学生化残差",ylab = "百分比") #画正态概率图
}
ei = resid(fm)
ti = ti(ei,X) #计算外部学生化残差ti
plot_ZP(ti) #绘制正态概率图
plot(fitted(fm),ti) #绘制残差与所预测y_pred的残差图
abline(h = 0)
#绘制除去5,6两点的正态概率图
data = data[-c(5,6),]
x = data$x
y = data$y
X = cbind(1,x)
fm1 = lm(y~x) #线性模型
ei = resid(fm1)
ti = ti(ei,X) #计算外部学生化残差ti
plot(fitted(fm1),ti) #绘制残差与所预测y_pred的残差图
abline(h = 0)
#例4.8
data = read.xlsx("4.8.xlsx",sheet = 1)
x = data$x
y = data$y
fm = lm(y~x) #线性回归
a = anova(fm) #方差分析
sst = sum(a[2]) #总平方和
ssg = a[1,2] #回归平方和
sse = a[2,2] #残差平方和
level_x = c(table(x)>1) #查看哪些自变量重复
#进行失拟检验
library(rsm) #加载rsm包用于失拟检验
lm.rsm<-rsm(y~FO(x))
loftest(lm.rsm) #调用失拟检验函数loftest
rm(list = ls())
例4.10 通过近邻点估计纯误差
#例4.10
data = read.xlsx("3.1.xlsx",sheet = 1) #导入数据
names(data)=c("order","time","cases","distance")
y = data$time #准备数据
x1 = data$cases
x2 = data$distance
fm = lm(y~x1 + x2) #线性回归
coef(fm)
b_cases = coef(fm)[2] #beta1
b_distance = coef(fm)[3] #beta2
y_pred = predict(fm) #计算预测值
ei = resid(fm) #残差
new_data = cbind(data,y_pred,ei) #构建新数据
new_data = new_data[order(new_data$y_pred),] #按照预测值升序排序
a = anova(fm) #方差分析
sse = a[3,2] #残差平方和
mse = a[3,3] #残差均方和
#计算Dii'
Di_i = function(i,i_,mse,beta1,beta2,new_data) #i第i个点,i_第i_个点,data数据集
{
one = beta1*(new_data$cases[i]-new_data$cases[i_])/sqrt(mse)
two = beta2*(new_data$distance[i]-new_data$distance[i_])/sqrt(mse)
ans = one**2 + two**2
return(ans)
}
#定义一个数据框用来存储结果
σ_ans = data.frame(
i = numeric(0), #观测值i
i_ = numeric(0), #观测值i_
Dii = numeric(0), #Di_i
delta = numeric(0) #E|ei-ei_|
)
#计算相邻k个点的两点的 Di_i,i,i_,Delta残差
for (k in c(1:4))
{
for (i in c(1:24))
{
if (i+k>25)
break
D = Di_i(i,i+k,mse,b_cases,b_distance,new_data) #计算相邻k个点的两点的Di_i
E = abs(new_data$ei[i]-new_data$ei[i+k]) #计算相邻k个点的两点的Delta残差
another = data.frame(
i = new_data$order[i],
i_ = new_data$order[i+k],
Dii = D,
delta = E
)
σ_ans = rbind(σ_ans,another) #合并两个数据框
}
}
names(σ_ans) = c("i","i_","Dii^2","Delta") #重命名最后的数据框
σ_ans = σ_ans[order(σ_ans$Dii^2),] #按照Di_i对数据框进行排序
row.names(σ_ans) = c(1:90) #对每一行进行编号
#计算累计标准差
std = numeric(0) #存储累计标准差
sum_Delta = 0 #存储累计Delta残差
for (i in 1:90)
{
sum_Delta = sum_Delta + σ_ans$Delta[i] #0.886/m*Σ(Delta)
res = 0.886/i*sum_Delta
std[i] = res
}
σ_ans = cbind(std,σ_ans)
4.16
#######################自己编的函数,运行后直接调用#######################
#计算mse的函数
mse = function(ei,p) #ei是残差向量,p是回归参数个数
{
n = length(ei)
sse = sum(ei**2)
mse = sse/(n-p)
return(mse)
}
#计算帽子矩阵,并提取对角线元素
H = function(X) #X是回归向量矩阵
{
h = X%*%solve(t(X)%*%X)%*%t(X)
hii = diag(h)
return(hii)
}
#外部学生化残差
ti = function(ei,X) #输入残差回归变量矩阵
{
p = ncol(X) #回归参数个数
n = length(ei) #数据个数
hii = H(X) #帽子矩阵主对角线元素
s2_i = ((n-p)*mse(ei,p) -(ei**2)/(1-hii)) / (n-p-1) #计算S(i)^2
ans = ei / sqrt(s2_i*(1-hii))
return(ans)
}
#计算PRESS统计量
press = function(ei,X) #X是自变量的设计矩阵
{
hii = H(X)
res = sum((ei/(1-hii))**2)
#View(res)
}
#计算PRESS的预测R^2
R_pred = function(X,y)
{
hii = H(X)
ei = resid(lm(y~X[,2]+X[,3]))
PRESS = sum((ei/(1-hii))**2)
sst = sum((y-mean(y))**2)
ans = 1-PRESS/sst
return(ans)
}
#绘制正态概率图
plot_ZP = function(ti) #输入外部学生化残差
{
n = length(ti)
order = rank(ti) #按升序排列,t(i)是第order个
Pi = (order-1/2)/n #累积概率
plot(ti,Pi,xlim=c(-3,3),xlab = "学生化残差",ylab = "百分比") #画正态概率图
}
#进行失拟检验
library(rsm) #加载rsm包用于失拟检验
lm.rsm<-rsm(y~FO(x))
loftest(lm.rsm) #调用失拟检验函数loftest
#计算Dii'
Di_i = function(i,i_,mse,beta1,beta2,new_data) #i第i个点,i_第i_个点,data数据集
{
one = beta1*(new_data$cases[i]-new_data$cases[i_])/sqrt(mse)
two = beta2*(new_data$distance[i]-new_data$distance[i_])/sqrt(mse)
ans = one**2 + two**2
return(ans)
}
#4.16
#a.残差的正态概率图
data = read.xlsx('3.12.xlsx',sheet = 1) #导入数据
y = data$y
x1 = data$x1
x2 = data$x2
X = cbind(1,x1,x2) #处理数据
fm = lm(y~x1+x2) #线性回归模型
ei = resid(fm) #计算残差
ti = ti(ei,X) #ti()自制求外部学生化残差函数
plot_ZP(ti) #plot_zp()自制绘制正态概率图函数
#为什么要编写函数?
#1.这些题目都是重复的代码操作
#2.如果是想多次重复打代码来熟悉,大可不必,因为会忘的。
#正态概率图有一个异常点,order(ti) 返回第一小的是第28号点
#b.残差与响应变量预测值的残差图
plot(fitted(fm),ti)
#残差图表明残差包含在一条水平带中,模型不存在明显的缺点。
#c.
#模型fm的PRESS统计量
press_fm = press(ei,X)
#新模型fm1的PRESS统计量
fm1 = lm(y~x2)
ei = resid(fm1)
X = cbind(1,x2)
press_fm1 = press(ei,X) #press()自制求press统计量函数
#选择press统计量小的模型