之前我们说单独讲了数组这种数据结构,从底层的存储结构上来说,与数组对应的就是链表这种数据结构了。因为这两者都是非常基础、非常常用的数据结构。所以我想趁着刚总结完数组之后开始总结链表这种数据结构。
第一斧:啥是链表?
维基百科上对链表的描述是这样的:
链表(Linked list)是一种常见的基础数据结构,是一种线性表,但是并不会按线性的顺序存储数据,而是在每一个节点里存到下一个节点的指针(Pointer)。由于不必须按顺序存储,链表在插入的时候可以达到O(1)的复杂度,比另一种线性表顺序表快得多,但是查找一个节点或者访问特定编号的节点则需要O(n)的时间,而顺序表相应的时间复杂度分别是O(logn)和O(1)。
使用链表结构可以克服数组链表需要预先知道数据大小的缺点,链表结构可以充分利用计算机内存空间,实现灵活的内存动态管理。但是链表失去了数组随机读取的优点,同时链表由于增加了结点的指针域,空间开销比较大。
常见的几种链表结构:
- 单向链表
- 双向链表
- 循环链表
我们知道,在进行数组的插入、删除操作时,为了保持内存数据的连续性,需要做大量的数据搬移,所以时间复杂度是 O(n)。而在链表中插入或者删除一个数据,我们并不需要为了保持内存的连续性而搬移结点,因为链表的存储空间本身就不是连续的。所以,在链表中插入和删除一个数据是非常快速的。
但是由于链表的数据在内存中是非连续的,所以它无法做到像数组那样支持随机访问。那么结合我们之前讨论的插入和删除操作我们来想一想,如果我在链表中删除或者在指定位置插入一个节点的时间复杂度真的是O(1)吗?
虽然链表的插入和删除操作不像数组那样需要对数据进行搬移,只需要考虑相邻结点的指针改变,所以对应的时间复杂度是 O(1)。但是,我们删除或者插入操作之前的第一步是先找到这个节点。为了找到这个节点,我们只能对链表进行遍历,而这个遍历操作的时间复杂度是O(n)。所以我们应该说链表单纯的插入或删除操作时间复杂度是O(1),但是查找到需要删除元素或者需要插入的位置的时间复杂度是O(n),根据时间复杂度的加法法则,所以整体时间复杂度为O(n)。
第二斧:画图理解链表
说到这里大家对链表是不是已经有一个初步的印象了,如果没有也不要紧。我们针对常见的三种链表画图表示一下,相信你一下就明白了。
单向链表
链表通过指针将一组零散的内存块串联在一起。其中,我们把内存块称为链表的“结点”。为了将所有的结点串起来,每个链表的结点除了存储数据之外,还需要记录链上的下一个结点的地址。如图所示,我们把这个记录下个结点地址的指针叫作后继指针 next。如图:
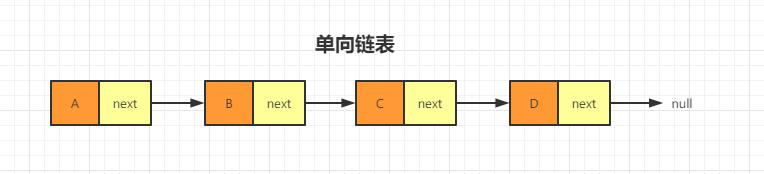
大家看到这个图就会发现有两个节点是比较特殊的分别是A节点和D节点,因为A节点没有节点指向它,D节点的后继指针指向了NULL,而A节点和D节点又分别是这个单向链表中的第一个和最后一个节点。我们习惯性的称第一个节点叫头节点,最后一个节点叫尾节点。
双向链表
单向链表只有一个方向,结点只有一个后继指针 next 指向后面的结点。而双向链表,顾名思义,它支持两个方向,每个结点不止有一个后继指针 next 指向后面的结点,还有一个前驱指针 prev 指向前面的结点。双向链表需要额外的两个空间来存储后继结点和前驱结点的地址。所以,如果存储同样多的数据,双向链表要比单链表占用更多的内存空间。
不要觉得它只是在浪费内存空间哦,这样设计肯定是有意义的。从结构上来看,双向链表可以支持 O(1) 时间复杂度的情况下找到前驱结点,正是这样的特点,也使双向链表在某些情况下的插入、删除等操作都要比单链表简单、高效。
那双向链表的数据结构在图上是怎么表示的呢?
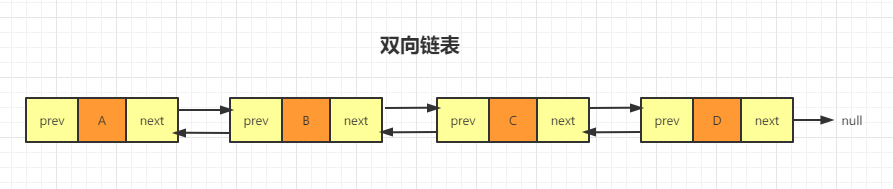
循环链表
还记得刚才我们说链表中存在两个特殊节点:
- 头节点
- 尾节点
但是,我们考虑一下,每一种链表都存在这两个节点吗?大家肯定在神话或者游戏中听说过衔尾蛇这个名词吧。它是一个古代流传下来的符号,形象为一条蛇吞食自己的尾巴,结果形成一个圆环(有时亦会展示成扭纹形,即“∞”)如果我们将链表的首尾相连会发生什么呢?
其实首尾相连(尾节点的后继指针指向头节点)的链表就叫做循环链表了。如图所示:
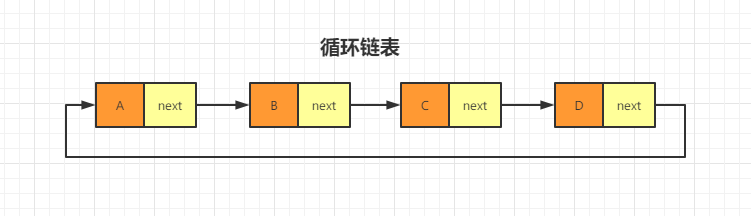
看到这,大家可能已经发现了。这个循环链表就是单向链表的循环链表啊,如果是双向链表可以做循环链表吗?答案当然是可以的,你可以自己画一下试试。
第三斧:show me the code
基本结构
看完前面对单向链表的描述,大家在脑海中肯定对其有一定的了解了,那么我们尝试将脑海中对单向链表的理解翻译成代码试试。
public class Node{
// 节点中存储的值
private int data;
// 节点的后继指针
private Node next;
}
那我们说完单向链表,是不是双向链表的结构也呼之欲出了呢?你可以尝试手写一个然后和我进行比较。
public class Node{
// 节点中存储的值
private int data;
// 节点的前驱指针
private Node prev;
// 节点的后继指针
private Node next;
}
是不是很简单。那我们在逐步加大难度。
插入链表节点
如果我希望你在一个存在链表最后插入一个新的节点,节点的值为10。用代码怎么实现?
解体思路:
-
我们需要先遍历链表node,先找到尾节点
-
将尾节点的后继指针指向值为10的新节点。
public void insert(Node node, int val){
Node tempNode = node;
while(tempNode.next != null){
tempNode = tempNode.next;
}
tempNode.next = new Node(10);
}
刚才我们是在尾节点之后插入了一个新节点,那如果我们希望在链表中第n个节点之后插入一个新的节点怎么办呢?
解题思路:
- 遍历链表node,找到第n个节点
- 将其的后继指针指向的节点进行存储(新建一个Node temp 存储)
- 将其后继指针指向新节点
- 将新节点的后继指针指向temp
- 退出循环
public void insert(Node node, int index, int val){
Node p = node;
int i = 0;
while(p != null){
if(i == index){
Node temp = p.next;
p.next = new Node(val);
p.next.next = temp;
}
p = p.next;
i++;
}
}
删除链表节点
刚才说完了插入,我们再来看一下删除。对于链表来说其实合理的删除只有四种情况:
- 删除头节点
- 删除尾节点
- 删除第N个节点
- 删除值为xxx的节点
现在我们分别看一下,首先是删除头节点和尾节点,这个比较简单,我就一起说了
// 删除头节点
public void deleteHeadNode(Node node){
node = node.next;
}
// 删除尾节点
public void deleteTailNode(Node node){
Node p = node;
Node prev = null;
while(p.next != null){
prev = p;
p = p.next;
}
prev.next = null;
}
然后我们尝试来写一下删除第N个节点
public void deleteByIndex(Node node, int index){
int i = 0;
Node p = node;
Node prev = null;
while(p != null){
if(i == index){
prev.next = p.next == null ? null : p.next.next;
}
i++;
prev = p;
p = p.next;
}
}
最后我们来尝试写一下删除所有值为val的节点
private static Node deleteByVal(Node node, int val){
if (node.val == val) {
node = node.next;
}
Node p = node;
Node prev = node;
while(p != null){
if(p.val == val){
prev.next = p.next;
}
prev = p;
p = p.next;
}
return node;
}
我到现在依然觉得在了解数据结构和算法构想之后,如果你遇到看不明白的代码算法或者算法问题,举例画图是最快理解的办法。所以如果对上面的代码你有任何不太理解的地方都可以通过举例画图的方式来理解。当然也欢迎你留言给我,我看到之后会第一时间回复的。