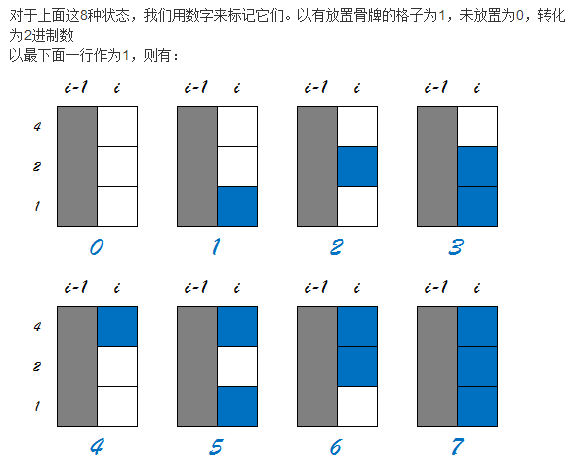
http://hihocoder.com/contest/hiho42/problem/1
给定一个n,问我们3*n的矩阵有多少种覆盖的方法
第41周做的骨牌覆盖是2*n的,状态转移方程是dp[i] = dp[i-1] + dp[i-2],递推数列可以用矩阵快速幂来加速计算
我们可以用状态dp来做这一题,如果某个格子上被铺了骨牌,就标记为1,否则为0
那么每一列一共有8个状态。
两种状态的表示法
第一种:
dp[i][s] 表示填满第i行后,第i+1行的状态为s,
那么s的转移情况如下,
0->1,4,7
1->0,6
2->5
3->4
4->0,3
5->2
6->1
7->0
那么就可以构造出转换的矩阵
1 int mat[8][8] = { 2 { 0, 1, 0, 0, 1, 0, 0, 1 }, 3 { 1, 0, 0, 0, 0, 0, 1, 0 }, 4 { 0, 0, 0, 0, 0, 1, 0, 0 }, 5 { 0, 0, 0, 0, 1, 0, 0, 0 }, 6 { 1, 0, 0, 1, 0, 0, 0, 0 }, 7 { 0, 0, 1, 0, 0, 0, 0, 0 }, 8 { 0, 1, 0, 0, 0, 0, 0, 0 }, 9 { 1, 0, 0, 0, 0, 0, 0, 0 } 10 };
初始时,只有状态0存在,状态1,2,3,4,5,6,7都不存在
所以初始的向量为 A = [1,0,0,0,0,0,0,0,0]
转换n次后为, A*mat^n
转化n次后,获得的是第i+1行的不同状态的个数,我们要的是第i+1行状态为0的个数,即A[0]

1 #include <stdio.h> 2 #include <string.h> 3 #include <stdlib.h> 4 #include <algorithm> 5 #include <iostream> 6 #include <queue> 7 #include <stack> 8 #include <vector> 9 #include <map> 10 #include <set> 11 #include <string> 12 #include <math.h> 13 using namespace std; 14 #pragma warning(disable:4996) 15 typedef long long LL; 16 const int INF = 1 << 30; 17 const int MOD = 12357; 18 /* 19 20 */ 21 int mat[8][8] = { 22 { 0, 1, 0, 0, 1, 0, 0, 1 }, 23 { 1, 0, 0, 0, 0, 0, 1, 0 }, 24 { 0, 0, 0, 0, 0, 1, 0, 0 }, 25 { 0, 0, 0, 0, 1, 0, 0, 0 }, 26 { 1, 0, 0, 1, 0, 0, 0, 0 }, 27 { 0, 0, 1, 0, 0, 0, 0, 0 }, 28 { 0, 1, 0, 0, 0, 0, 0, 0 }, 29 { 1, 0, 0, 0, 0, 0, 0, 0 } 30 }; 31 int mat2[8][8] = { 32 { 1, 0, 0, 0, 0, 0, 0, 0 }, 33 { 0, 1, 0, 0, 0, 0, 0, 0 }, 34 { 0, 0, 1, 0, 0, 0, 0, 0 }, 35 { 0, 0, 0, 1, 0, 0, 0, 0 }, 36 { 0, 0, 0, 0, 1, 0, 0, 0 }, 37 { 0, 0, 0, 0, 0, 1, 0, 0 }, 38 { 0, 0, 0, 0, 0, 0, 1, 0 }, 39 { 0, 0, 0, 0, 0, 0, 0, 1 }, 40 }; 41 struct Matrix 42 { 43 int mat[8][8]; 44 Matrix() 45 { 46 memset(mat, 0, sizeof(mat)); 47 } 48 }; 49 Matrix operator*(const Matrix &lhs, const Matrix &rhs) 50 { 51 Matrix ret;//零矩阵 52 for (int i = 0; i < 8; ++i) 53 { 54 for (int j = 0; j < 8; ++j) 55 { 56 for (int k = 0; k < 8; ++k) 57 { 58 ret.mat[i][j] = (ret.mat[i][j] + lhs.mat[i][k] * rhs.mat[k][j]) % MOD; 59 } 60 } 61 } 62 63 return ret; 64 } 65 Matrix operator^(Matrix a, int n) 66 { 67 Matrix ret;//单位矩阵 68 for (int i = 0; i < 8; ++i) 69 { 70 for (int j = 0; j < 8; ++j) 71 ret.mat[i][j] = mat2[i][j]; 72 } 73 while (n) 74 { 75 if (n & 1) 76 { 77 ret = ret * a; 78 } 79 n >>= 1; 80 a = a * a; 81 } 82 return ret; 83 } 84 85 int main() 86 { 87 int n; 88 while (scanf("%d", &n) != EOF) 89 { 90 91 Matrix a; 92 for (int i = 0; i < 8; ++i) 93 { 94 for (int j = 0; j < 8; ++j) 95 a.mat[i][j] = mat[i][j]; 96 } 97 a = a^n; 98 cout << a.mat[0][0] << endl; 99 100 } 101 return 0; 102 }
第二种转换方法为:
dp[i][s]表示填满第i-1行时,第i行的状态为s
同样的,可以得到转化的矩阵, 其实,两种转化的方法就是转化矩阵的不同

1 #include <stdio.h> 2 #include <string.h> 3 #include <stdlib.h> 4 #include <algorithm> 5 #include <iostream> 6 #include <queue> 7 #include <stack> 8 #include <vector> 9 #include <map> 10 #include <set> 11 #include <string> 12 #include <math.h> 13 using namespace std; 14 #pragma warning(disable:4996) 15 typedef long long LL; 16 const int INF = 1<<30; 17 const int MOD = 12357; 18 /* 19 20 */ 21 int mat[8][8] = { 22 { 0, 0, 0, 0, 0, 0, 0, 1 }, 23 { 0, 0, 0, 0, 0, 0, 1, 0 }, 24 { 0, 0, 0, 0, 0, 1, 0, 0 }, 25 { 0, 0, 0, 0, 1, 0, 0, 1 }, 26 { 0, 0, 0, 1, 0, 0, 0, 0 }, 27 { 0, 0, 1, 0, 0, 0, 0, 0 }, 28 { 0, 1, 0, 0, 0, 0, 0, 1 }, 29 { 1, 0, 0, 1, 0, 0, 1, 0 } 30 }; 31 int mat2[8][8] = { 32 { 1, 0, 0, 0, 0, 0, 0, 0 }, 33 { 0, 1, 0, 0, 0, 0, 0, 0 }, 34 { 0, 0, 1, 0, 0, 0, 0, 0 }, 35 { 0, 0, 0, 1, 0, 0, 0, 0 }, 36 { 0, 0, 0, 0, 1, 0, 0, 0 }, 37 { 0, 0, 0, 0, 0, 1, 0, 0 }, 38 { 0, 0, 0, 0, 0, 0, 1, 0 }, 39 { 0, 0, 0, 0, 0, 0, 0, 1 }, 40 }; 41 struct Matrix 42 { 43 int mat[8][8]; 44 Matrix() 45 { 46 memset(mat, 0, sizeof(mat)); 47 } 48 }; 49 Matrix operator*(const Matrix &lhs, const Matrix &rhs) 50 { 51 Matrix ret;//零矩阵 52 for (int i = 0; i < 8; ++i) 53 { 54 for (int j = 0; j < 8; ++j) 55 { 56 for (int k = 0; k < 8; ++k) 57 { 58 ret.mat[i][j] = (ret.mat[i][j] + lhs.mat[i][k] * rhs.mat[k][j]) % MOD; 59 } 60 } 61 } 62 63 return ret; 64 } 65 Matrix operator^(Matrix a, int n) 66 { 67 Matrix ret;//单位矩阵 68 for (int i = 0; i < 8; ++i) 69 { 70 for (int j = 0; j < 8; ++j) 71 ret.mat[i][j] = mat2[i][j]; 72 } 73 while (n) 74 { 75 if (n & 1) 76 { 77 ret = ret * a; 78 } 79 n >>= 1; 80 a = a * a; 81 } 82 return ret; 83 } 84 85 int main() 86 { 87 int n; 88 while (scanf("%d", &n) != EOF) 89 { 90 n += 2; 91 Matrix a; 92 for (int i = 0; i < 8; ++i) 93 { 94 for (int j = 0; j < 8; ++j) 95 a.mat[i][j] = mat[i][j]; 96 } 97 a = a^n; 98 cout << a.mat[7][7] << endl; 99 100 } 101 return 0; 102 }
