这是一个连续更新的系列。。。。。。。。。。。
冒泡排序
冒泡排序:依次比较数组中相邻的两个元素,如果左边比右边大则进行调换,以此类推,这样第一次排序就把最大的元素放在最底下
伪代码:
1 do 2 swapped = false 3 for i = 1 to indexOfLastUnsortedElement-1 4 if leftElement > rightElement 5 swap(leftElement, rightElement) 6 swapped = true; swapCounter++ 7 while swapped
详细过程:

选择排序
选择排序:每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完。
选择排序是不稳定的排序方法(比如序列[5, 5, 3]第一次就将第一个[5]与[3]交换,导致第一个5挪动到第二个5后面)。

插入排序
插入排序:每步将一个待排序的纪录,按其关键码值的大小插入前面已经排序的文件中适当位置上,直到全部插入完为止

归并排序
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
归并过程为:比较a[i]和b[j]的大小,若a[i]≤b[j],则将第一个有序表中的元素a[i]复制到r[k]中,并令i和k分别加上1;否则将第二个有序表中的元素b[j]复制到r[k]中,并令j和k分别加上1,如此循环下去,直到其中一个有序表取完,然后再将另一个有序表中剩余的元素复制到r中从下标k到下标t的单元。归并排序的算法我们通常用递归实现,先把待排序区间[s,t]以中点二分,接着把左边子区间排序,再把右边子区间排序,最后把左区间和右区间用一次归并操作合并成有序的区间[s,t]。

快速排序
快速排序:通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
随机快速排序
随机快速排序:是快速排序的一种优化,即使用随机的位置作为快速排序的主元(快速排序是使用第一个数作为主元)
计数排序
计数排序是一个非基于比较的排序算法,该算法于1954年由 Harold H. Seward 提出。它的优势在于在对一定范围内的整数排序时,它的复杂度为Ο(n+k)(其中k是整数的范围),快于任何比较排序算法。
当然这是一种牺牲空间换取时间的做法,而且当O(k)>O(n*log(n))的时候其效率反而不如基于比较的排序(基于比较的排序的时间复杂度在理论上的下限是O(n*log(n)), 如归并排序,堆排序)
基数排序

排序算法消耗时间
消耗时间参考该文章https://www.cnblogs.com/woider/p/6835466.html,在此表示感谢
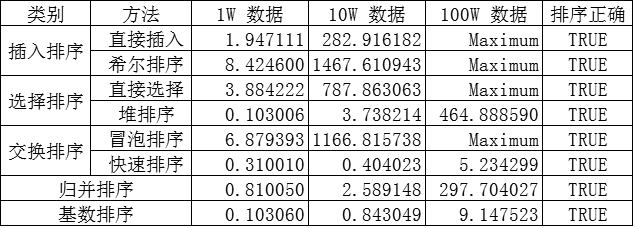
选择
有序的数据结构中插入数据在排序,一般使用插入排序;
取序列中最大最小的几个数时,一般使用选择排序;
要求时间最短时,一般使用快速排序;
内存少的时候,可以进行并行计算的时候,一般使用归并排序;
使用大量数,并且数据的位数很大时,一般使用基数排序;
冒泡一般都不用;