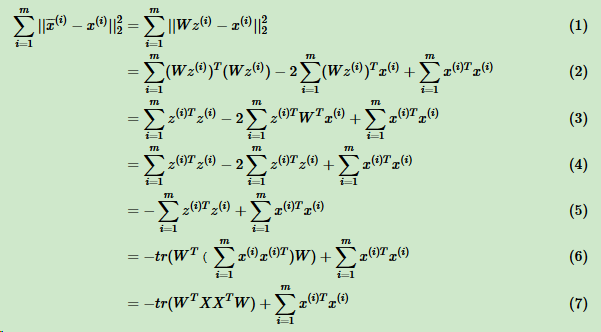来自:刘建平
主成分分析(Principal components analysis,以下简称PCA)是最重要的降维方法之一。
1. PCA的思想
PCA顾名思义,就是找出数据里最主要的方面,用数据里最主要的方面来代替原始数据。
我们降维的标准为:样本点到这个超平面的距离足够近,或者说样本点在这个超平面上的投影能尽可能的分开。
基于上面的两种标准,我们得到PCA的两种等价推导。
2. PCA的推导:基于最小投影距离
第一种:样本点到这个超平面的距离足够近。
假设m个n维数据  都已经进行了中心化,即
都已经进行了中心化,即 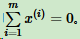 经过投影变换得到新坐标系为
经过投影变换得到新坐标系为  ,其中w为标准正交基,即
,其中w为标准正交基,即 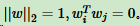
如果我们将数据从n维降到n'维,即丢弃新坐标系中的部分坐标,则新的坐标系为  ,样本点 x(i) 在 n' 维坐标系中的投影为:
,样本点 x(i) 在 n' 维坐标系中的投影为: 其中,
其中,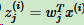 是x(i)在低维坐标系里第 j 维的坐标。
是x(i)在低维坐标系里第 j 维的坐标。
如果我们用 z(i) 来恢复原始数据 x(i) ,则得到的恢复数据 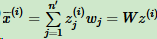 ,其中,w为标准正交基组成的矩阵。
,其中,w为标准正交基组成的矩阵。
现在考虑整个样本集,我们希望所有的样本到这个超平面的距离足够近,即最小化式:
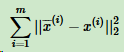
将这个式子整理: