Critical Connections in a Network (H)
题目
There are n servers numbered from 0 to n-1 connected by undirected server-to-server connections forming a network where connections[i] = [a, b] represents a connection between servers a and b. Any server can reach any other server directly or indirectly through the network.
A critical connection is a connection that, if removed, will make some server unable to reach some other server.
Return all critical connections in the network in any order.
Example 1:
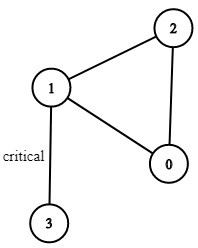
Input: n = 4, connections = [[0,1],[1,2],[2,0],[1,3]]
Output: [[1,3]]
Explanation: [[3,1]] is also accepted.
Constraints:
1 <= n <= 10^5n-1 <= connections.length <= 10^5connections[i][0] != connections[i][1]- There are no repeated connections.
题意
在无向图中找到所有的边,使得删去该边后,存在两结点无法互相到达。
思路
tarjan算法,求所有的"桥"。
代码实现
Java
class Solution {
private Map<Integer, List<Integer>> graph;
private boolean[] visited;
private int[] dfn;
private int[] low;
private int num;
public List<List<Integer>> criticalConnections(int n, List<List<Integer>> connections) {
graph = new HashMap<>();
visited = new boolean[n];
dfn = new int[n];
low = new int[n];
num = 0;
List<List<Integer>> ans = new ArrayList<>();
for (List<Integer> edge : connections) {
int a = edge.get(0);
int b = edge.get(1);
graph.putIfAbsent(a, new ArrayList<>());
graph.putIfAbsent(b, new ArrayList<>());
graph.get(a).add(b);
graph.get(b).add(a);
}
tarjan(0, -1, ans);
return ans;
}
private void tarjan(int cur, int parent, List<List<Integer>> ans) {
visited[cur] = true;
dfn[cur] = num++;
low[cur] = dfn[cur];
for (int next : graph.get(cur)) {
if (!visited[next]) {
tarjan(next, cur, ans);
low[cur] = Math.min(low[cur], low[next]);
// 满足条件时说明删去改变子结点和父结点将不在同一个连通分量中
if (low[next] > dfn[cur]) ans.add(Arrays.asList(cur, next));
} else if (next != parent) { // 必须排除与父结点的边
low[cur] = Math.min(low[cur], dfn[next]);
}
}
}
}