Card Collector

题源

---

题面

 

---

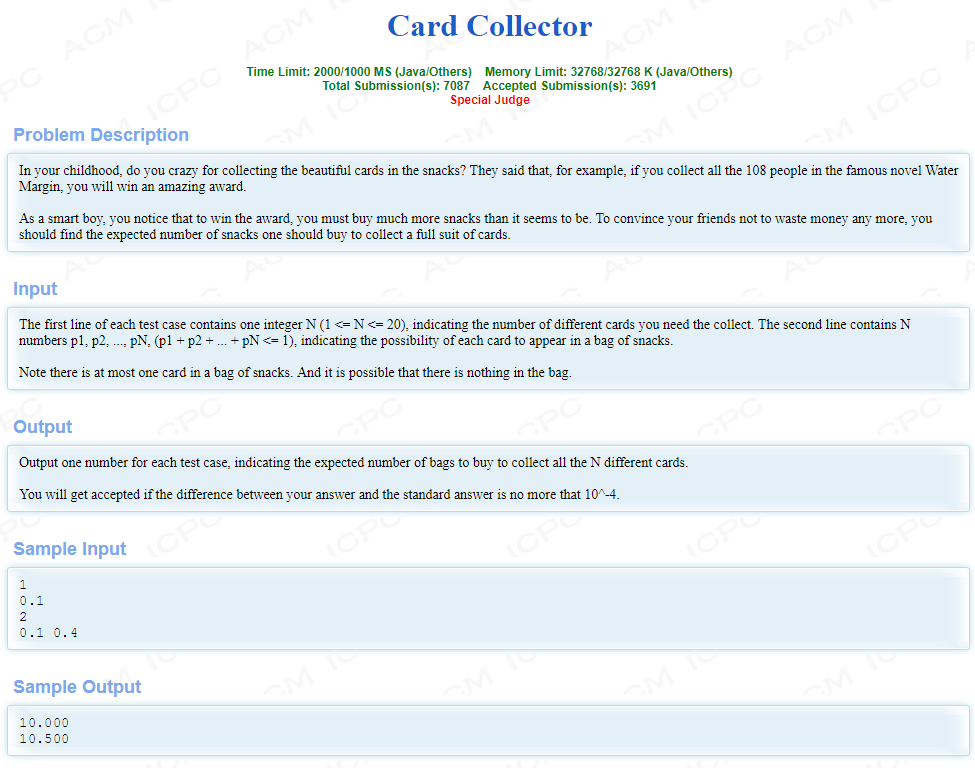
1.状压 O( n* 2^n )

我们记录 f[s]为已经取完 s 时的期望时间

若取到了，加上新取到的概率

不然则加上什么也取不到的概率

Code:

#include<stdio.h>
#include<string.h>
#define For(i,a,b) for(register int i=(a);i<=(b);i++)
using namespace std;
const int maxn=21;
int n;
double f[1<<maxn],p[maxn];
signed main(){
    while(~scanf("%d",&n)){
        For(i,0,n-1){
            scanf("%lf",&p[i]);
        }
        int mx=(1<<n)-1;f[mx]=0;
        for(register int s=mx;~s;s--){
            double tx=0;f[s]=0;
            For(i,0,n-1){
                if(~s&(1<<i)){
                    f[s]+=f[s|(1<<i)]*p[i],tx+=p[i];
                }
            }
            if(tx) f[s]=(f[s]+1)/tx;
        }
        printf("%.4lf
",f[0]);
    }
}

  

---

 Min-Max容斥  O( 2^n )

因为期望有可加性， 所以与普通的Min-Max长得一样

Code:

#include<stdio.h>
#include<string.h>
#define For(i,a,b) for(register int i=(a);i<=(b);i++)
using namespace std;
const int maxn=21;
int n;
double ans,p[maxn];
inline void dfs(int i,double sum,double opt){
    if(i==n){
        if(sum>=1e-9) ans+=opt/sum;
        return ;
    }
    dfs(i+1,sum,opt),dfs(i+1,sum+p[i],-opt);
}
signed main(){
    while(~scanf("%d",&n)){
        For(i,0,n-1){
            scanf("%lf",&p[i]);
        }
        ans=0;dfs(0,0,-1);
        printf("%.4f
",ans);
    }
}