Backpropagation - 走看看

zoukankan html css js c++ java

Backpropagation
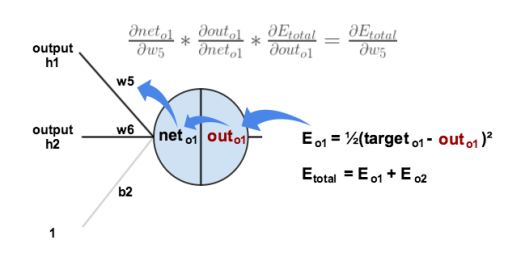
一般都是用链式法则解释
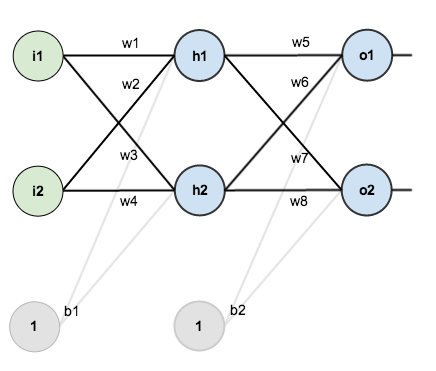
比如如下的神经网络

前向传播

对于节点 $h_1$ 来说， $h_1$ 的净输入 $net_{h_1}$ 如下：
$net_{h_1}=w_1 imes i_1+w_2 imes i_2+b_1 imes 1$
接着对 $net_{h_1}$ 做一个sigmoid函数得到节点 $h_1$ 的输出：
$out_{h_1}=frac{1}{1+e^{-net_{h_1}}}$
类似的，我们能得到节点 $h_2$ 、 $o_1$ 、 $o_2$ 的输出 $out_{h_2}$ 、 $out_{o_1}$ 、 $out_{o_2}$ 。

误差

得到结果后，整个神经网络的输出误差可以表示为：
$E_{total}=sumfrac{1}{2}(target-output)^2$
其中 $output$ 就是刚刚通过前向传播算出来的 $out_{o_1}$ 、 $out_{o_2}$ ； $target$ 是节点 $o_1$ 、 $o_2$ 的目标值。 $E_{total}$ 用来衡量二者的误差。
这个 $E_{total}$ 也可以认为是cost function，不过这里省略了防止overfit的regularization term（ $sum{w_i^2}$ ）
展开得到
$E_{total}=E{o_1}+E{o_2}=frac{1}{2}(target_{o_1}-out_{o_1})^2+frac{1}{2}(target_{o_2}-out_{o_2})^2$

后向传播

对输出层的 $w_5$

通过梯度下降调整 $w_5$ ，需要求 $frac{partial {E_{total}}}{partial {w_5}}$ ，由链式法则：
$frac{partial {E_{total}}}{partial {w_5}}=frac{partial {E_{total}}}{partial {out_{o_1}}}frac{partial {out_{o_1}}}{partial {net_{o_1}}}frac{partial {net_{o_1}}}{partial {w_5}}$ ，
如下图所示：
$frac{partial {E_{total}}}{partial {out_{o_1}}}=frac{partial}{partial {out_{o_1}}}(frac{1}{2}(target_{o_1}-out_{o_1})^2+frac{1}{2}(target_{o_2}-out_{o_2})^2)=-(target_{o_1}-out_{o_1})$
$frac{partial {out_{o_1}}}{partial {net_{o_1}}}=frac{partial }{partial {net_{o_1}}}frac{1}{1+e^{-net_{o_1}}}=out_{o_1}(1-out_{o_1})$
$frac{partial {net_{o_1}}}{partial {w_5}}=frac{partial}{partial {w_5}}(w_5 imes out_{h_1}+w_6 imes out_{h_2}+b_2 imes 1)=out_{h_1}$
以上3个相乘得到梯度 $frac{partial {E_{total}}}{partial {w_5}}$ ，之后就可以用这个梯度训练了：
$w_5^+=w_5-eta frac{partial {E_{total}}}{partial {w_5}}$
很多教材比如Stanford的课程，会把中间结果 $frac{partial {E_{total}}}{partial {net_{o_1}}}=frac{partial {E_{total}}}{partial {out_{o_1}}}frac{partial {out_{o_1}}}{partial {net_{o_1}}}$ 记做 $delta_{o_1}$ ，表示这个节点对最终的误差需要负多少责任。。所以有 $frac{partial {E_{total}}}{partial {w_5}}=delta_{o_1}out_{h_1}$ 。

对隐藏层的 $w_1$

通过梯度下降调整 $w_1$ ，需要求 $frac{partial {E_{total}}}{partial {w_1}}$ ，由链式法则：
$frac{partial {E_{total}}}{partial {w_1}}=frac{partial {E_{total}}}{partial {out_{h_1}}}frac{partial {out_{h_1}}}{partial {net_{h_1}}}frac{partial {net_{h_1}}}{partial {w_1}}$ ，
如下图所示：
参数 $w_1$ 影响了 $net_{h_1}$ ，进而影响了 $out_{h_1}$ ，之后又影响到 $E_{o_1}$ 、 $E_{o_2}$ 。
求解每个部分：
$frac{partial {E_{total}}}{partial {out_{h_1}}}=frac{partial {E_{o_1}}}{partial {out_{h_1}}}+frac{partial {E_{o_2}}}{partial {out_{h_1}}}$ ，
其中 $frac{partial {E_{o_1}}}{partial {out_{h_1}}}=frac{partial {E_{o_1}}}{partial {net_{o_1}}} imes frac{partial {net_{o_1}}}{partial {out_{h_1}}}=delta_{o_1} imes frac{partial {net_{o_1}}}{partial {out_{h_1}}}=delta_{o_1} imes frac{partial}{partial {out_{h_1}}}(w_5 imes out_{h_1}+w_6 imes out_{h_2}+b_2 imes 1)=delta_{o_1}w_5$ ，这里 $delta_{o_1}$ 之前计算过。
$frac{partial {E_{o_2}}}{partial {out_{h_1}}}$ 的计算也类似，所以得到
$frac{partial {E_{total}}}{partial {out_{h_1}}}=delta_{o_1}w_5+delta_{o_2}w_7$ 。
$frac{partial {E_{total}}}{partial {w_1}}$ 的链式中其他两项如下：
$frac{partial {out_{h_1}}}{partial {net_{h_1}}}=out_{h_1}(1-out_{h_1})$ ，
$frac{partial {net_{h_1}}}{partial {w_1}}=frac{partial }{partial {w_1}}(w_1 imes i_1+w_2 imes i_2+b_1 imes 1)=i_1$
相乘得到
$frac{partial {E_{total}}}{partial {w_1}}=frac{partial {E_{total}}}{partial {out_{h_1}}}frac{partial {out_{h_1}}}{partial {net_{h_1}}}frac{partial {net_{h_1}}}{partial {w_1}}=(delta_{o_1}w_5+delta_{o_2}w_7) imes out_{h_1}(1-out_{h_1}) imes i_1$
得到梯度后，就可以对 $w_1$ 迭代了：
$w_1^+=w_1-eta frac{partial{E_{total}}}{partial{w_1}}$ 。
在前一个式子里同样可以对 $delta_{h_1}$ 进行定义， $delta_{h_1}=frac{partial {E_{total}}}{partial {out_{h_1}}}frac{partial {out_{h_1}}}{partial {net_{h_1}}}=(delta_{o_1}w_5+delta_{o_2}w_7) imes out_{h_1}(1-out_{h_1}) =(sum_o delta_ow_{ho}) imes out_{h_1}(1-out_{h_1})$ ，所以整个梯度可以写成 $frac{partial {E_{total}}}{partial {w_1}}=delta_{h_1} imes i_1$

=======================
上述 $delta$ 就是教程Unsupervised Feature Learning and Deep Learning Tutorial 中第三步计算的由来。。

所谓的后向传播，其实就是『将来在宣传传播上出了偏差，你们要负责的！』，每一个节点负责的量用 $delta$ 表示，那么，隐藏节点需要负责的量，就由输出节点负责的量一层层往前传导。
参考：
【1】A Step by Step Backpropagation Example
【2】Unsupervised Feature Learning and Deep Learning Tutorial
查看全文

相关阅读:
分布式编程下的CAS
《码农翻身》读后感
 PHP Socket服务器搭建和测试
 在Java中使用Hibernate，使用不同数据库服务名
 linq的表关系解决办法
 SilverLight中使用WCF Ria出现的问题empty domain service class
cmd中更换用户权限
 Flex中TabBar与ViewStack
使用ApdComPort
拖动控件

原文地址：https://www.cnblogs.com/mrxsc/p/6023083.html

Copyright © 2011-2022 走看看