无向图最短路径问题,是图论中最经典也是最基础的问题之一。本题我们考虑一个有 nn 个结点的无向图 GG。
GG 是简单完全图,也就是说 GG 中没有自环,也没有重边,但任意两个不同的结点之间都有一条带权的双向边。
每一条边的边权是非负实数,但我们并不知道每一条边的具体边权。
好消息是我们知道 GG 中任意两点最短路径的长度d(i,j)d(i,j)。且保证至少有一种边权的分配方案满足得到的带权图中ii与jj的最短路长度恰好是d(i,j)d(i,j)。
下面是留给你的任务:对于任意一对点(i,j)(i,j),希望你能找出来所有合法的边权分配方案中ii和jj之间边权的最大值。
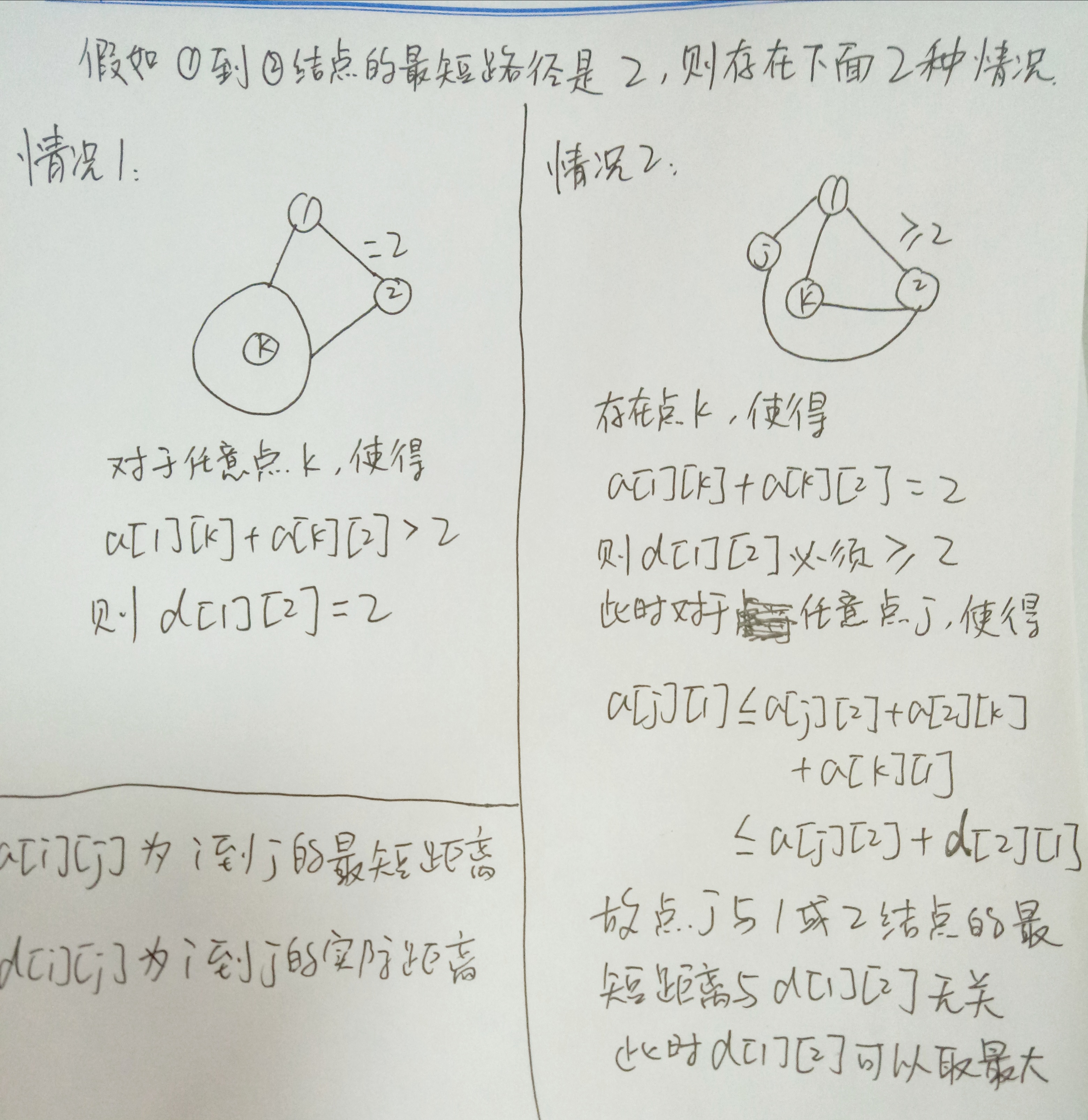
1 #include<iostream> 2 #include<string> 3 using namespace std; 4 5 int n,m; 6 int a[101][101],d[101][101]={0}; 7 8 int main() 9 { 10 cin>>n; 11 while(n--) 12 { 13 cin>>m; 14 for(int i=1;i<=m;++i) 15 for(int j=1;j<=m;++j) 16 cin>>a[i][j]; 17 18 for(int i=1;i<=m;++i) 19 for(int j=1;j<=m;++j) 20 if(i!=j) 21 { 22 int l=1000; 23 for(int k=1;k<=m;++k) 24 if(k!=i&&k!=j&&a[i][k]+a[k][j]<l) 25 l=a[i][k]+a[k][j]; 26 if(l==a[i][j]) d[i][j]=10000; 27 else d[i][j]=a[i][j]; 28 } 29 30 for(int i=1;i<=m;++i) 31 { 32 for(int j=1;j<=m;++j) 33 { 34 if(j!=1) cout<<" "; 35 if(d[i][j]==10000) cout<<"infty"; 36 else cout<<d[i][j]; 37 } 38 39 cout<<endl; 40 } 41 } 42 // system("pause"); 43 44 }