译者:本文为转载翻译自免费英文电子书《Neural Networks and Deep Learning》,将逐步翻译成中文,原文链接:http://neuralnetworksanddeeplearning.com/chap1.html
由于本章节很长,编辑器很卡,翻译时我会分成几个小节,这是第一小节。
人类的视觉系统是很神奇的。考虑一下下面几个手写的数字:
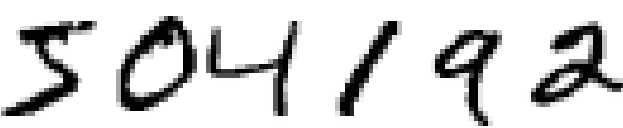
大多数人一眼就认出这些数字是504192。在人的每个大脑半球,人类有一个主要的视觉皮质,被称为 V1,包含 1.4亿个神经元, 有几百亿的神经连接。人类的视觉系统不单只涉及V1,而且涉及到一整个视觉皮质 - V2, V3, V4, 和 V5 - 它们一步步处理着复杂的图像。我们大脑是一个超级计算机,经过几十亿年的演变,逐渐适应这个可视化的世界。识别手写数字不是那么容易的。相反地,人类的处理能力是惊人的,人类善于使我们理解看到的东西。几乎所有工作都是无意识地进行。我们通常不会佩服自己的视觉系统怎样解决怎么困难的问题。视觉模式识别的困难性显而易见,如果你尝试写一个程序来识别类似下面数字。看起来简单的东西实现起来非常困难。简单直观的例子是我们怎么识别形状。 - "数字 9 头顶上有一个圈,右下方是一竖" - 用算法来表达不是那么容易的。当你尝试让这些规则变得很精确,你很快就会在异常、警告和例外的困境中蒙圈。它看起来毫无解决的希望。
神经网络以不同的方式解决这个问题。思路是拿大量的手写数字来作为训练样本,

然后演化为一个可以从样本中学习的系统,从另外的角度来讲,神经网络使用样本来自动推理手写识别的规则。进一步,通过增加训练样本,网络可以学习更多手写文字,改善它识别的准确度。我只是在上面展示了100个用于训练的数字,也许我们可以通过使用几千、几百万、几十亿的训练样本来建一个更好的手写识别器。
在这一节,我们会写一个程序来实现一个学习手写数字的神经网络。这个程序只有74行代码,并且没有用到第三方的神经网络库。但这个小程序的识别精度可以达到96%,而且是在没有人的介入的情况下达到的。然后进一步,在接下来的章节中,我们会改进,使程序的精度达到99%。事实上,最好的商业应用神经网络可以应用在银行的账单处理中,以及邮局的地址识别。
我们专注于讲解手写识别,因为这是一个学习神经网络的非常棒的原型。手写识别作为学习例子有个好处:有挑战性 - 识别手写数字是一个不小的本领 - 但不需要非常复杂的解决方案,也不需要海量计算那么困难。进一步讲,这是一个发展高级计算,例如深度学习的很好的途径。这这本书的整个过程,我们会重复地提到手写识别的问题。这本书的后面,我们会讨论怎样将这些思想应用到计算机视觉方面,人机对话和自然语言处理,以及其他领域。
当然,如果这节的关键在于写一个程序来识别手写数字,那么这节内容会短很多。但在此期间,我们会引出很多关键的神经网络思想,包括两种重要的人工神经网络 (感知网络和 sigmoid 神经网络),以及标准的神经网络学习算法,例如梯度下降算法。在此期间,我会集中讲解为什么神经网络的原理,让你从直观上认识神经网络。 我不止给你简单展示基本的机制,我需要啰嗦一大段。啰嗦是值得的,希望你会理解更加深刻。 从这章节,你可以理解什么是深度学习,为什么它那么重要。
感知器
什么是神经网络?为了开始,我会解释一种叫感知网络的神经网络。感知网络在1950到1960左右被科学家 Frank Rosenblatt提出,它受到 Warren McCulloch 和 Walter Pitts早期研究成果的启发。 今天,这种网络以及被其它种类的神经网络代替了 - 在这本书中,更加先进的主流使用的神经网络是sigmoid 神经网络。 我们很快就介绍到它了。但为了明白为什么会出现 sigmoid 网络,首先要明白什么是感知网络。
那么感知网络是怎样工作的呢? 感知网络有一个或以上的输入 x1,x2,…之有一个二进制输出:
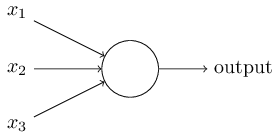
在下面的例子,展示了感知网络有三个输入, x1,x2,x3。通常可能少于或者多于三个输入。 Rosenblatt 提出一个简单地规则来计算输出值。他引入了权重, w1,w2,…用一个真实的数值表达各个输入到输出的重要性。神经元的输出 0 或者 1,取决于是否的权重的和∑jwjxj小于或者大于阈值。就像权重,阈值也是一个数值,它是神经元的一个参数之一。用更加精确的算法术语来表达:
输出=0 如果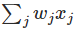 ≤ 阈值
≤ 阈值
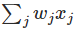 > 阈值
> 阈值这就是感知网络的工作原理!
这是基本的数学模型。你可以这样理解感知网络,它是一个通过衡量各种因素的重要程度来作决定的设备。 我举个例子,不是很现实的例子,但人容易明白,稍后我们会了解到更加现实的例子。假如周末要来了,你听说你所在将举办一个奶酪节 。你很喜欢奶酪,你纠结是否要去这个奶酪节看看。你可能会衡量三个因素来决定是否要去:
- 天气是否下雨
- 你的男朋友或者女朋友会不会陪你去
- 奶酪节现场是否有公共交通工具 (假如你没有私家车)
我们可以通过三个二进制变量来呈现这三个因素 x1,x2, and x3。举例, x1=1 如果天气晴朗, x1=0 表示天气很糟糕。 类似地 x2=1 表示你的男/女朋友想陪你去,x2=0 表示不陪你去。 x3x3 表示公共交通状况以此类推。
现在,假如你非常喜欢奶酪, 你当然乐于去奶酪节现场,即使你男/女朋友对此不感兴趣,或者交通不是特别方便。但可能你非常讨厌下雨天,如果下雨的话你对什么节之类丧失兴趣。你可以用感知网络来作这种决策的建模。其中的一个建模方法是选择一个圈子 w1=6 w1=6用来代表天气的权重, w2=2和 w3=2代表其它条件的权重。最大的权重w1表明天气对你的决定影响很大。它比朋友和交通情况都要重要。最后,假如你选择了一个阈值5。这样感知网络的决策模型的建模就完成了。输出1,当天气好,当天气坏输出0。 无聊朋友是否陪伴还是交通状况都无法影响你最后的决定。
通过不同的权重和阈值,我们可以得到不同的决策模型。例如,假如你的阈值选了3。那么感知网络会认为你应该去,无论天气情况、交通状况、是否有朋友陪伴。换言之,这变成了另外一个决策模型了。减少阈值意味着你更想去奶酪节。
显然,感知网络不是人类完整的决策模型。但至少证明了感知网络可以通过设置不同条件的权重来做决策。而且它看起来可以通过复杂的网络来作出稳定的决策:
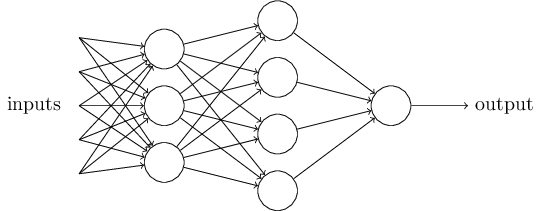
(2016-03-24待续)在这个网络,第一列 - 这里我们称为第一层 - 通过衡量输入条件的权重来作出三个简单的决策。第二层是什么表示什么呢?每一个感知器都是通过衡量第一层作出的决定来作出一个新的决策。在这种情况,第二层网络可以作出比较复杂,比第一层更加抽象的决策,在第三层网络可以作出更加复杂的判断。这样看来,有多层网络的感知机可以作出很复杂决策。
很意外,当我定义感知网络的时候,我说过感知网络只有一个输出。在上面的感知网络看起来好像有很多个输出。事实上,它们依然只有一个输出。多个输出都指向下一个网络作为下一个网络的输入。 画一条想然后分开两条并不难。
我们简化地描述感知器。 ∑jwjxj>阈值这个条件显得很累赘,我们用两个符号变换来简化它。第一个变换是将∑jwjxj用点来表示, w⋅x≡∑jwjxj,w 和x是一个向量,分别表示权重和输入值。第二个变换是将阈值移动到不等式的另一边。用偏移量来代替表示阈值 b≡−threshold。 这样感知器就可以表示为:
你可以将偏移量看成感知器输出1的容易程度。或者用生物学的角度来说,是激活感知器的的容易程度。偏移量越大,越容易输出1,反之很难输出1。(2016-3-25待续)明显,引入了偏移量对于描述感知器是一个很小的变化,但我们会在后面看到这会导致进一步的符号简化。因为这个,这篇文字的余下内容我们不再使用阈值这个概念,取代之的是偏移量。
我将感知器描述为衡量各种因素来做决策的一种方法。感知器也可以用于计算基本的逻辑函数例如 与门AND, 或门 OR, 和 与非门NAND。例如,假如你有一个感知器有两个输入的,每一个输入的权重都是-2,偏移量为3。像下面这样:
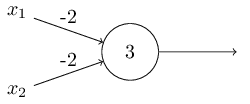
我们可以看到输入0和0时输出1,因为(−2)∗0+(−2)∗0+3=3 输出值为正数。类似的计算输入0和1 输出1,但是输入1和1的时候会输出0,因为 (−2)∗1+(−2)∗1+3=−1 是负数。这样的话感知器就可以实现与非门了!
与非门 NAND的例子表明我们可以使用感知器来计算简单的逻辑功能。事实上,我们可以使用感知器的网络来计算任何的逻辑函数。因为非门在计算机领域是通用的,也就是说我们可以使用非门来实现任意计算。例如我们可以使用非门来建立一个用于两个位相加的回路,x1和x2。这需要计算按位相加x1⊕x2,当x1 和 x2都为1 移位运算后值为1:
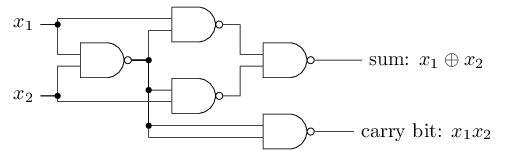
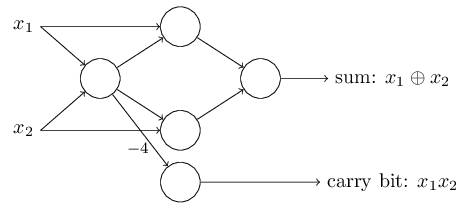
为了得到一个等效于非门逻辑的两个输入的感知器,我们将两个输入的权重都设为-2,偏移量设为3。如下图所示:
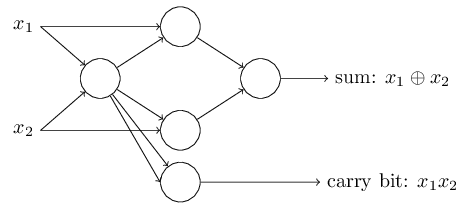
这个感知器要注意的是输出从最左边的感知器被使用了两次作为输入到最底部的感知器。当我定义一个感知器模型,我不会说是否两个输入指向同一个地方的做法是否正确。事实上,没有关系。如果我们不想允许这种做法,那么你简单的合并这两天线就行了,这样就变成了一个权重为-4的连接了,而不是两个各有-2权重的连接。(如果你看不明白,你应该先停一下,慢慢推理证实一下这两者是否等效) 经过这样的变化之后,网络就看起来如下图所示了, 全部都有没有标出的权重 -2,所以偏移量等于3,其中一个的权重是-4, 标记出来是这样的:
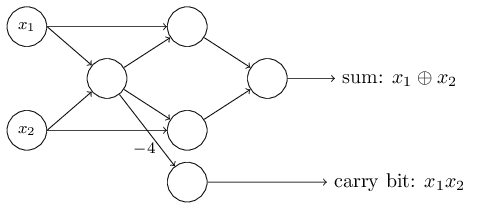
到现在为止,我已经在网络的左边出了输入如x1和x2作为变量。事实上,按照惯例我们会画出一个额外的感知器的层 - 输入层 - 用来编码这些输入:
这个符号用来表示输入感知器,只有输出没有输入,
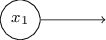
这是一个简写。并不真正意味着感知器没有输入。为了看到这个,假如我们有一个没有输入的感知器。那么权重加起来∑jwjxj 会总是0,如果 b>0感知器会输出1 ,如果 b≤0输出0。感知器会简单地输出一个固定的值,不是想要的值 (x1,在下面的例子中)。 你把输入感知器看错不是真的感知器比较好,但相当特殊的单元,被简单地定义输出想要的值 x1,x2,…。
加法器的例子证明了一个感知器怎样用于模拟一个包含很多个与非门的电路。因为与非门 NAND 对于计算是通用的,所以可以说感知器对计算也是通用的。
感知器的计算通用性同时令人安慰和失望。令人安慰是因为它告诉我们感知器网络可以和其它计算设备那么强大。但令人失望的是,因为它看起来仅仅是一种新的与非门。这几乎不上什么大新闻!
然而,情况比看起来要好。结果是我们可以设计出可以自动调整神经网络权重和偏移量的学习算法。这种调整发生在响应外界的刺激时,没有程序员的直接介入。这个学习算法可以让我们通过一种完全不同与传统逻辑门的方式来使用神经网络。而不是明确的与非门和其它逻辑门的电路层,我们的神经网络可以简单的学会解决问题,特别是对于那些直接设计传统电路很难解决的难题。
S型神经元(Sigmoid neurons )
学习算法听起来很了不起。但是我们怎样给神经网络设计出这样算法呢?假如我们有一个想用来学习解决问题的感知器神经网络。 例如,网络的输入可能是来自扫描机或者手写数字的图片像素数据。我们想让网络学习权重和偏移量,网络的输出可以正确的分类这些数字。为了能看见学习是怎样开展的,我们假设在权重(或者偏移量)上面作一个小的改动,这个小的改动会相应的引起输出的一个变化。我们一会之后就可以看到,这个特性会让学习成为可能。下图就是我们想要的 (明显这个网络对于手写识别过于简单):
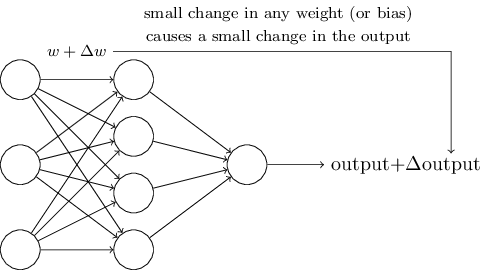
如果这是真的,一个权重或者偏移量的值得一个小的变化只会引起输出的一个小的变化,那么我们可以用这个机制类改变权重和偏移量让升级网络以我们想的方式来表现。例如,假如网络错误地将数字9识别为8。我们可以计算出怎样改变权重和偏移量,让网络的识别结果偏向的正确的9。然后我们会重复这样调整,改变权重和偏移量,让输出原来越正确。这样的话,网络就有学习的能力了。
问题是感知器不能实现这种微调的的效果。事实上,权重或者偏移量的一个微小的变化有时候会导致输出结果意想不到的改变,该输出0的输出了1,改输出1的输出了0。当你调整网络的权重或者偏移量使数字图片 "9" 能正确的被分类,其它图片的分类可能因此被打乱了。这使我们很难通过微调权重和偏移量来让网络接近我们想要的结果。也许会有一些聪明的方法来避免这个问题。
我们可以通过引入一种叫做S型神经元的新的人工神经元来解决这个问题。S型神经元类似于感知器,但是经过了改造,从而能够使得权重和偏移量的小的变化会对输出产生小的影响。这个关键的特性使得是S型神经元具有学习能力。
好,让我妈描述一下S型神经元。 我们会已面试感知器的形式类描述S型神经元:

就像感知器,S型神经元可以有多个输入 x1,x2,…。但是输入不只是0或者1,而是0到1之间的任意值。例如 0.638…是S型神经元的有效的输入。就像感知器,S型神经元每个输入都有对应的权重 w1,w2,…,和全局的偏移量b。输出也不只是0或者1,而是 σ(w⋅x+b),σ 被称为 sigmoid 函数。顺便说一下 σ 有时又被称为 逻辑函数,这种新的神经元叫逻辑神经元。记住这个术语是很有用的,因为这个术语在神经网络界经常被用到。我们会继续介绍sigmoid ,它被定义为
为了更加清晰,它的输入x1,x2,…,权重 w1,w2,…以及偏移量b表示如下:
一眼看去,它和感知器有很大的不同。这个代数公司看起来晦涩难懂,除非你很熟悉它。事实上,它和感知器有很多类似的地方。
为了明白它和感知器的相似性,假如 z≡w⋅x+b是一个很大的正数。 e−z≈0, 那么σ(z)≈1。换言之,当 z=w⋅x+b是一个很大的正数,那么S型神经元输出接近1,就像感知器那样。假如z=w⋅x+b是一个很小的复数。那么 e−z→∞,那么 σ(z)≈0。感知器也有类似的特性。只有当w⋅x+b 是最合适的大小时才会有最大的偏离来自于感知器模型。
代数式σ是什么鬼?怎样理解它?事实上,σ 的准确形式并不重要 - 重要的是它的曲线图。这就是它的曲线图形状:

这个形式就是阶梯函数平滑一点的版本:

如果σ 是一个阶梯函数,那么S型神经元就变成了一个感知器,因为输出只能是1或者0,这取决于是否 w⋅x+b为正或者负数。事实上当w⋅x+b=0 感知器输入为0,而阶梯函数则输出1。严格来说,我们需要改造一下阶梯函数。但你明白这种思想。通过使用真实的σ函数,上面提到的那个,一个平滑的感知器。事实上, σ函数的平滑性是决定性的,不是公式的细节本身。σ的平滑性意味着细微的权重变化Δwj和偏移量变化Δb会引起神经元的一个很小的输出变化 Δoutput。事实上微积分告诉我们
总和是全局的权重wj, ∂output/∂wj和 ∂output/∂b各自贡献输出值的一部分导数。不要惊慌如果你不适应部分导数,上面的表达式看似复杂,全都是部分导数,它事实上是表示了一些很简单的东西(好消息):Δoutput 是权重变化Δwj和偏移量变化Δb的一个线性函数。 线性特质使得权重和偏移量的小变化可以达到想要的输出的微小变化。因此S型神经元和感知器在性质上相似的,它们更容易算出怎样通过改变权重和偏移量来改变输出值。
如果σ 的曲线图真的很重要而不是公式,那么为什么使用使用这个特定的公式呢?事实上,在本书的后面,我们会提一下输出为f(w⋅x+b) 的其它激活函数的神经元。使用其它激活函数的不同点是部分导数的特别地值 在等式(5)改变。 在任何情况下, σ在神经网络领域是通用的,它是我们这本书中最常使用的激活函数。
我们应该怎么诠释S型神经元的输出呢?明显,一个很大不同是S型神经元不只是输出0或者1。它们可以输出0到1之间的任意小数值例如0.173… ,0.689…等是合法的输出。这个很有用,例如,如果我们想使用输出值来代表输入图片的平均像素的灰度。 但有时可能会很烦人。假如我们想表示"输入图片是9" 或者 "输入图片不是9"。明显在感知器中很容易用输出是0或者1来表示。但实践中,我们可以指定规矩来处理,例如,通过决定解释任何输出至少为0.5就表示识别为"9",任意小于0.5的输出表示这个图片不是 9。我会总是明确地表述当我们使用这样的规定,因此不会导致混淆。
练习题
- Sigmoid神经元用来仿真感知器 第一部分
假如我们拿感知器所有的权重和偏移量乘以一个正数c,告诉我网络的行为为什么不变。
- Sigmoid神经元用来仿真感知器 第二部分
假如我们和上面的问题的条件一样 - 一个感知器网络。假如全部输入被选择。我们不需要时间输入的值,我们只是需要输入固定的值。假如对于输入值x,权重和偏移量计算结果 w⋅x+b≠0 。现在用S型神经元替换所以的感知器,权重和偏移量乘以一个正数c。算出极限 c→∞,S神经元网络的行为是否和感知器网络的相同。为什么会失败当 w⋅x+b=0感知器会?
神经网络的架构
在下一节我会介绍一个可以很好地分类手写数字的神经网络。作为预热,我们先熟悉一些术语。假如我们有一个网络:
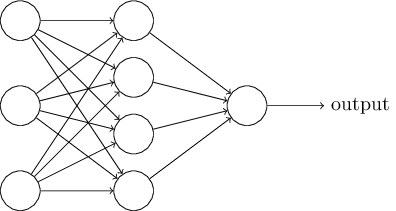
如早些提到的,最左边的叫输入层,其中的神经元叫输入神经元。最右边的输出层包含的是输出神经元。在上图中只有一个输出神经元。两层之间的叫隐藏层, - 我第一次听到这个名词是我我想肯定会有深层的哲学或者数学意思 - 但真的没有什么特别意思,还不如说这是“非输入非输出层”。上图的网络只有一个隐藏层,但某些网络可能有很多个隐藏层。例如,下面的四层网络有两个隐藏层:
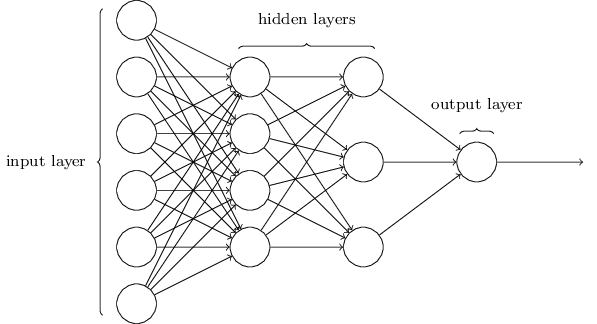
可能会让人迷惑的是,基于历史的原因,一些多层网络有时候被称为多层神经元MLP。 不管是否有sigmoid神经元或者感知器组成, 我不会继续使用MLP这个术语了。我认为他让人搞不懂,但我提醒你一下,有这么一个名词。
输入输出层的设计通常是很直观的。例如,假如我们尝试判断手写数字图片是否是9.一个很自然的方法是实际一个网络将图片的像素的颜色长度转换为数字输入神经网络。如果图片是 64X64的灰度图片,那么我们就有 4,096=64×64个输入神经元,灰度数字在0 和1之间。输出层只有一个神经元,输出小于0.5则表示这个图片不是9,反之这个图片就是9。
我们也可以很有技巧地设计一个隐藏层。尤其,将隐藏层处理结果用简单的规则加起来的比较困难的。神经网络研究者已经发明了很多设计探索法设计隐藏层,帮助人们设计出能获得想要的输出结果的网络。这些方法可以用来帮助决定怎样权衡隐藏层的数量和时间需求。我们会在后面介绍几个这样的方法。
迄今为止,我们邮件讨论输出用于下一层输入的神经网络。这样的网络叫做前馈网络。这意味着网络中没有循环 - 信息总是向前传递,不会往回传递。如果我们有了循环,我们就打破σ函数依赖于输出这个情形。这样很没意义,我们不允许这样的循环。
然而,有很多神经网络模型可以有反馈的循环。这些模型称为递归神经网络。这些模型的思想是让神经元在某个时间段内激活,然后转为非激活状态。激活可以模拟其它迟点激活的神经元。这样导致了级联式的神经元激活。在这个模型中循环不会有问题,因为输出只会在一段时间后影响输入,不是立刻。
递归神经网络比前馈网络的影响力小,某方面原因是递归神经网络的算法(至少到现在)还没显现出巨大威力。但他仍然非常有意思。因为它们比前馈网络更接近大脑的工作原理。而且它可能可以解决对于前馈网络很难解决的问题。然而,基于文本章节限制,我们暂时不讨论这个,我们集中讨论广泛应用的前馈网络。
继续阅读第一章的第二小节: http://www.cnblogs.com/pathrough/p/5322736.html