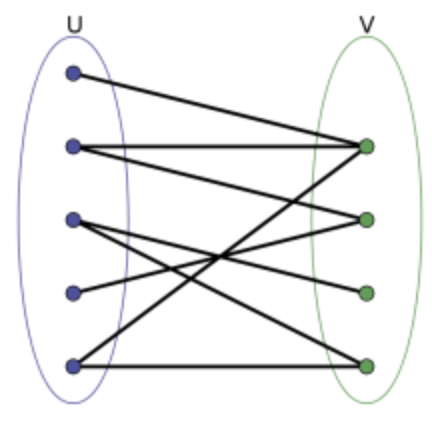
二分图定义
二分图又称作二部图,是图论中的一种特殊模型。 设G=(V,E)是一个无向图,如果顶点V可分割为两个互不相交的子集(A,B),并且图中的每条边(i,j)所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B),则称图G为一个二分图。简而言之,就是顶点集V可分割为两个互不相交的子集,并且图中每条边依附的两个顶点都分属于这两个互不相交的子集,两个子集内的顶点不相邻。(摘自百度百科)
边独立集(即匹配)的定义

截图摘自:MOOC 集合论与图论(下)
二分图(即偶图)的完全匹配和完美匹配
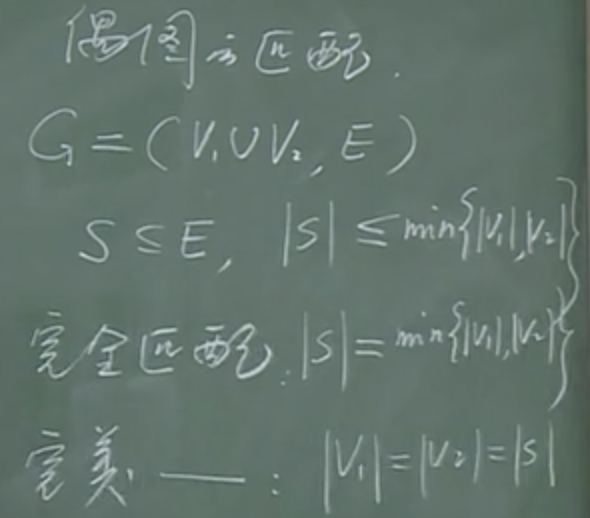
截图摘自:MOOC 集合论与图论(下)
二分图匹配的条件

匈牙利算法
代码:
from scipy.optimize import linear_sum_assignment
import numpy as np
cost = np.array([[4, 1, 3, 6], [2, 0, 5, 1], [3, 2, 2, 8], [4, 3, 2, 9]])
row_ind, col_ind = linear_sum_assignment(cost)
print('row_ind:')
print(row_ind) # 开销矩阵对应的行索引
print('col_ind:')
print(col_ind) # 对应行索引的最优指派的列索引
print('cost:')
print(cost[row_ind, col_ind]) # 提取每个行索引的最优指派列索引所在的元素,形成数组
print('cost_sum:')
print(cost[row_ind, col_ind].sum()) # 最小开销
运行结果:
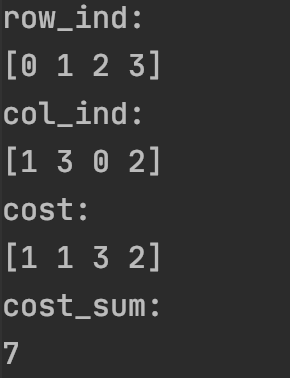
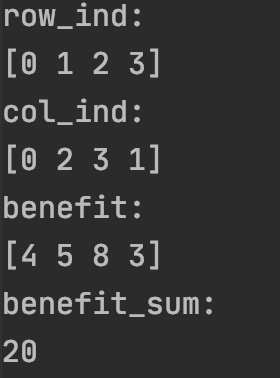
上述代码是把矩阵当做开销矩阵,希望求得最小开销;如果把矩阵当做收益矩阵,则希望得到最大收益,这时可以矩阵前面添加一个负号,以求得最大收益的分配。
from scipy.optimize import linear_sum_assignment
import numpy as np
cost = np.array([[4, 1, 3, 6], [2, 0, 5, 1], [3, 2, 2, 8], [4, 3, 2, 9]])
cost = -cost
row_ind, col_ind = linear_sum_assignment(cost)
print('row_ind:')
print(row_ind) # 收益矩阵对应的行索引
print('col_ind:')
print(col_ind) # 对应行索引的最优指派的列索引
print('benefit:')
print(-cost[row_ind, col_ind]) # 提取每个行索引的最优指派列索引所在的元素,形成数组
print('benefit_sum:')
print(-cost[row_ind, col_ind].sum()) # 最大收益
运行结果: