最小生成树:
求一个有 n 个结点的连通图的生成树是原图的极小连通子图,且包含原图中的所有 n 个结点,并且有保持图连通的最少的边.
1:Prim算法(适合稠密图)
伪代码:
Prim(G){ //G为图
int addnow[maxen];//记录当前有多少点被纳入集合;
int lowcost[maxen]; //记录当前集合中的点到其他点的最小距离的边集合;
init();//初始化点集合与边集合;
addnow[start]=true; //将起点纳入点集合
for(i=1;i<G.vertex;i++){ //还剩下n-1个点需要归并
Min=99999;
for(j=1;j<=G.vertex;j++){
if(!addnow[j]&&lowcost[j]<minn) { //寻找权值最小并且点未被归并的边
minn=addnow[j];
index=j; }
}
addnow[index]=1; //将该点加入集合
updateV();//因为点集合新入点,故需要更新该集合到其他点的距离
}
}
解析: 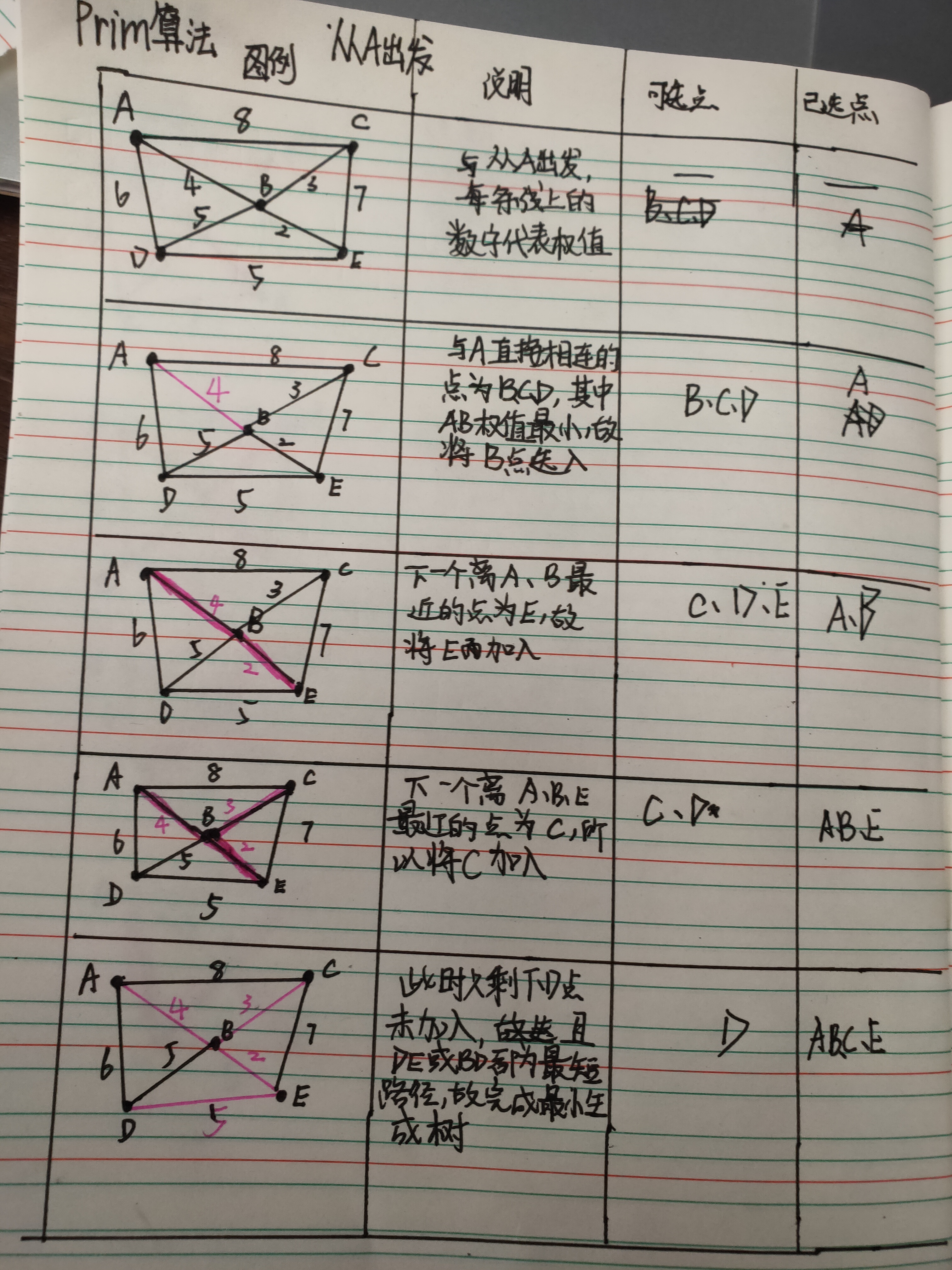
时间复杂度:O(n²)
Kruskal算法(适合稀疏图)
伪代码:(n为顶点数)
Kruskal(G){ for(i->G.edge.num){ if(find([G.edge.start])!=find([G.edge.end])){ //若没形成闭环 find([G.edge.end])=find([G.edge.start]); //将边加入路径 } if(edgeNum==G.vertex.num-1) //若已经找到n-1条边则退出 break; } }
解析:
时间复杂度:o(nlogn)
github源码地址: