回归问题:主要用于预测数值型数据,典型的回归例子:数据拟合曲线,回归算法中算法的最终结果是一个连续的数据值,输入值是一个d维度的属性/数值向量
一.线性回归
线性回归的定义:
线性回归需要一个线性模型,属于监督学习,因此方法和监督学习应该是一样的,先给定一个训练集,根据这个训练集学习出一个线性函数,然后测试这个函数是否足够拟合训练集数据,然后挑选出最好的函数.
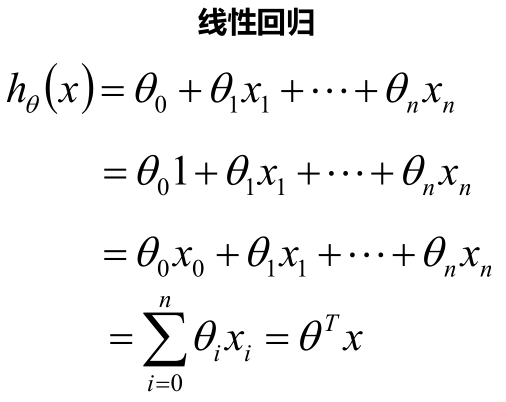
最终要求是计算出θ的值,并选择最优的θ值构成算法公式
怎么样能够看出线性函数拟合的好不好呢?
答案是我们需要使用到Cost Function(代价函数),代价函数越小,说明我们线性回归的越好,和训练数据拟合的越好。
线性回归、最大似然估计及二乘法
似然函数:在英语语境里,likelihood 和 probability 的日常使用是可以互换的,都表示对机会 (chance) 的同义替代。但在数学中,probability 这一指代是有严格的定义的,即符合柯尔莫果洛夫公理 (Kolmogorov axioms) 的一种数学对象(换句话说,不是所有的可以用0到1之间的数所表示的对象都能称为概率)。而 likelihood (function) 这一概念是由Fisher提出,他采用这个词,也是为了凸显他所要表述的数学对象既和 probability 有千丝万缕的联系,但又不完全一样的这一感觉。 中文把它们一个翻译为概率(probability),一个翻译为似然(likelihood)也是独具匠心。
似然函数的定义: L(θ|x) = f(x|θ)
上式中,小x指的是联合样本随机变量X取到的值,即X= x;这里的θ是指未知参数,它属于参数空间;而 是一个密度函数,特别地,它表示(给定)θ下关于联合样本值x的联合密度函数。 从定义上,似然函数和密度函数是完全不同的两个数学对象:前者是关于θ的函数,后者是关于x的函数。所以这里的等号= 理解为函数值形式的相等,而不是两个函数本身是同一函数(根据函数相等的定义,函数相等当且仅当定义域相等并且对应关系相等)。
两者的联系:
如果X是离散随机变量,那么其概率密度函数可改写为:
即代表了在参数为θ下,随机变量X取到x的可能性。并且,如果我们发现:
那么似然函数就反应出这样一个朴素推测:在参数下随机向量X取到值x的可能性大于在参数
下随机向量X取到值x的可能性。换句话说,我们更有理由相信相对于
来说
更有可能是真实值。这里的可能性是由概率来刻画。
综上,概率(密度)表达给定下样本随机向量X = x的可能性,而似然表达了给定样本X = x下参数
(相对于另外的参数
)为真实值的可能性。
最大似然估计:
在已知试验结果(即是样本)的情况下,用来估计满足这些样本分布的参数,把可能性最大的那个参数作为真实的参数估计。最大似然估计,最大似然估计是建立在这样的思想上:已知某个参数能使这个样本出现的概率最大,我们当然不会再去选择其他小概率的样本,所以干脆就把这个参数作为估计的真实值。
求最大似然函数估计值的一般步骤:
(1) 写出似然函数
(2) 对似然函数取对数,并整理
(3) 求导数
(4) 解似然方程
最小二乘法(Least Square )的解析解可以用 Gaussian 分布以及最大似然估计求得
首先假设线性回归模型具有如下形式:
其中:,
,误差
已知:
,
如何求参数W呢?
如果用最小二乘法的话,有误差函数:
我们对W求偏导,然后令个偏导 = 0,联立解方程——这就是最小二乘法求W的过程。
如果用最大似然函数求解的话:
假设误差服从高斯正态分布:
也就是说:
则最大似然估计推导:
对上式求偏导然后令个偏导 = 0,联立解方程。
总结:两者的结果是一样的。