一、JML知识梳理
JML是用于对java程序进行规格化设计的一种表示语言,通过JML及其支持工具,不仅可以基于规格自动构造测试用例,并整合了SMT Solver等工具以静态方式来检查代码实现对规格的满足情况。
-
JML理论基础
1. 注释结构
JML以注释的方式表示规格,每行都以@起头,有两种注释方式:行注释和块注释,如下所示:
1 //@行注释 2 3 /*@块注释 4 @块注释 5 @*/ 6
举例代码如下:
1 //@ public instance model non_null Path[] pList; 2 //@ public instance model non_null int[] pidList; 3 //@ public invariant pList.length == pidList.length; 4 //@ public constraint Math.abs(pList.length - old(pList.length)) <= 1; 5 6 /*@ public normal_behavior 7 @ requires containsPathId(pathId); 8 @ assignable othing; 9 @ ensures (exists int i; 0 <= i && i < pList.length; pidList[i] == pathId && esult == pList[i]); 10 @ also 11 @ public exceptional_behavior 12 @ requires !containsPathId(pathId); 13 @ assignable othing; 14 @ signals_only PathIdNotFoundException; 15 @*/ 16 public /*@pure@*/ Path getPathById(int pathId) throws PathIdNotFoundException;
以上JML规格分为两部分,1-4行是对JML所用变量的定义和限制,6-15行是对方法的JML说明。
第1行实例化了一个非空的Path数组pList,第2行实例化了一个非空的int数组pidList。第3,4行是对规格定义变量的限制,其中invariant不变式是对变量的静态限制,表明变量在静态状态下需要满足的要求,第3行表明pList和pidList的长度应一直保持相等;状态变化约束constraint是对变量的动态限制,第4行表明pList一次只能增加或减少一个元素。
第6-15行是方法getPathById的JML规格,也可分为两部分,第一部分是normal_behavior,正常行为规格;第二部分是exception_behavior,异常行为规格。无论是正常行为规格,还是异常行为规格,其核心内容主要包括三个方面:前置条件、后置条件和副作用约定。
- 前置条件:是对方法输入参数的限制,如果不满足前置条件,方法的执行结果不可预测,使用requires子句来表示:requires P;。例如第7行中只有满足containsPathId(pathId)为真,才能保证方法执行后符合正常行为规格的后置条件。
- 后置条件:是对方法执行结果的限制,如果满足后置条件,则表示方法执行正确,否则执行错误,使用ensures子句表示:ensures P;,例如第9行。
- 副作用范围限定:指方法在执行过程中对输入对象或者this对象进行了修改,常使用关键词assignable,例如第8行。
上述规格中的normal_behavior所指明的正常功能,一般指输入在正常范围内所对应的功能,而exceptional_behavior所定义的规格指明了异常功能,异常功能往往是当输入在正常范围之外时产生异常处理行为。在第10行中出现的also,表明除了正常功能规格之外,还有异常功能规格。
在异常功能规格中,后置条件常常表示为抛出异常,使用signals子句,结构为signals(***Exception e) expr,表明一旦满足表达式expr,就会抛出异常e。此外,还可以使用简化的signals子句,即signals_only子句,这个子句并不强调对象状态是否满足表达式,而是只要满足前置条件就抛出异常,例如第12、14行。
一个方法可以具有不止一个正常规格和异常规格。
此外,第16行中的/* pure */表示这个方法是纯粹查询方法,执行不会有任何副作用。
2. 常用表达式
esult:表示一个非void类型的方法执行所获得的结果,即方法执行后的返回值。 esult表达式的类型就是方法声明中定义的返回值的类型。
old(expr):表示表达式expr在相应方法执行前的取值。注意,如果v是一个对象,old(v)表示在方法执行前v的引用地址,并不包括v本身的内容。
forall:全称量词,可理解为“任意”,表示对于给定范围内的元素,每个元素都满足相应的约束。
exists:存在量词,表示对于给定范围内的元素,存在一个元素满足相应的约束。
sum:返回给定范围内表达式的和,例如:(sum int i; 0<=i && i< 5; i)得到的结果为0+1+2+3+4=10。
max:返回给定范围内表达式的最大值。
min:返回给定范围内表达式的最小值。
othing:表示一个空集,常常在副作用中使用,assignable othing表示这个方法没有副作用。
-
JML工具链
JML提供了许多工具,可以用于检验JML规格书写的正确性,也可以根据JML规格自动生成测试用例,工具大概有:
1. 使用OpenJML检查JML规格的正确性,提供对程序的静态和动态检查。
2, 使用SMT Solver验证代码等价性。
3. 使用JMLUnitNG自动生成测试数据验证代码的正确性。
二、JMLUnitNG使用体验
使用JMLUnitNG之前的文件树如下:

输入的命令行为:
java -jar ./jmlunitng.jar -cp ./lib/specs-homework-2-1.2-raw-jar-with-dependencies.jar ./src/*.java -d ./out/ ./src/MyGraph.java
执行之后的文件树如下,可见,JMLUnitNG工具自动生成了对每个类的测试:
out目录下均为自动构造的测试代码,截取部分如下,形如*_JML_TEST的java文件是对*类的TestNG测试文件:
在IDEA中编译并运行其中的MyGraph_JML_TEST.java文件,得到部分结果截取如下:
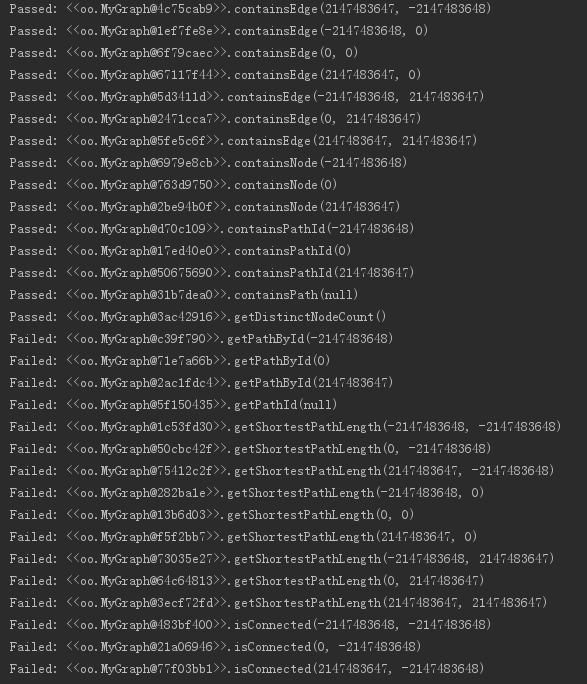
通过观察JMLUnitNG自动生成的测试用例发现,大多是对边界数据的测试,比如:0,2147483647,-2147483648,null。
通过分析输入数据,测试fail掉的原因主要是:
- 当输入中Id是小于等于0的数字时,方法没有给出确定的解决方案。
- 当输入的path是null时,方法没有判断并抛出异常。
三、作业架构分析
1. 第一次作业
第一次作业要求比较简单,比较难处理的方法是MyPathContainer中的getDistinctNodeCount。由于作业的指令数目比较大且有运行时间限制,并且增删路径的操作是有限的,这表明将会有大量的查询操作,又增删路径操作是不可避免的线性复杂度,因此可将对MyPathContainer中路径的维护放到涉及增删路径的方法中,而尽量降低查询操作的时间复杂度到O(1)。为了提高查询的速度,我在MyPathContainer中使用了如下结构维护路径。
private HashMap<Integer,Path> mapPidPath; private HashMap<Path,Integer> mapPathPid; private HashMap<Integer,Integer> mapNodePathNum;
其中,mapPidPath是pathId到path的映射,用于加速getPathByIid方法;mapPathPid是path到pathId的映射,用于加速getPathId方法;mapNodePathNum为结点到所属的路径数目的映射,即指出,“一个结点在几条路径中存在”,用于加速getDistinctNodeCount方法。每次增删路径时,需要维护以上三个结构,其中,mapNodePathNum结构的维护还需要依靠MyPath中的结构。MyPath中结构如下:
private ArrayList<Integer> nodes; private Set<Integer> distinctNodes;
其中,nodes用于按序记录路径中各结点,集合distinctNode用于记录路径中所有不重复的结点。在每次增删路径时,除了维护MyPathContainer中的前两个结构之外(这两个结构是比较好维护的),还需要维护第三个结构,而这个结构的维护需要获得MyPath中的不重复结点集合,并对于结点集合中的每个元素,改变其在mapNodePathNum中对应的路径数目。
第一次作业的类图如下:
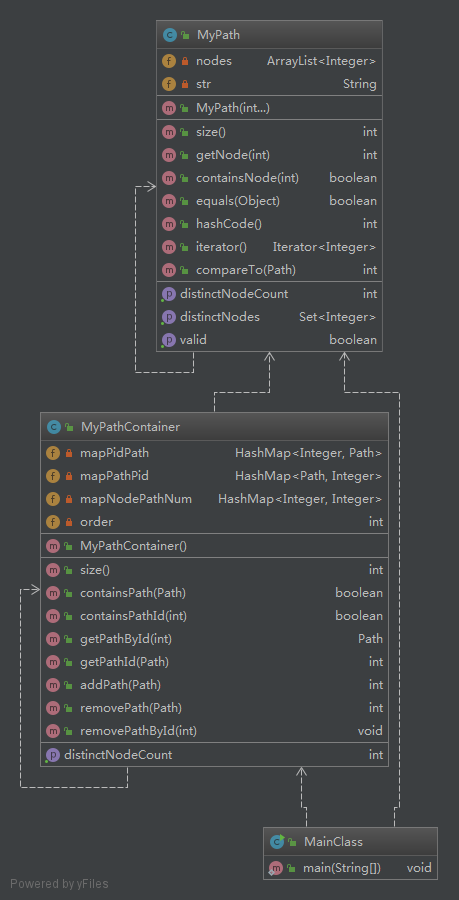
2. 第二次作业
第二次作业要求在第一次作业的基础上维护一个图,由于图的算法比较独立,于是我将图结构和最短路径算法单独封装成类。
第二次作业的类图如下:
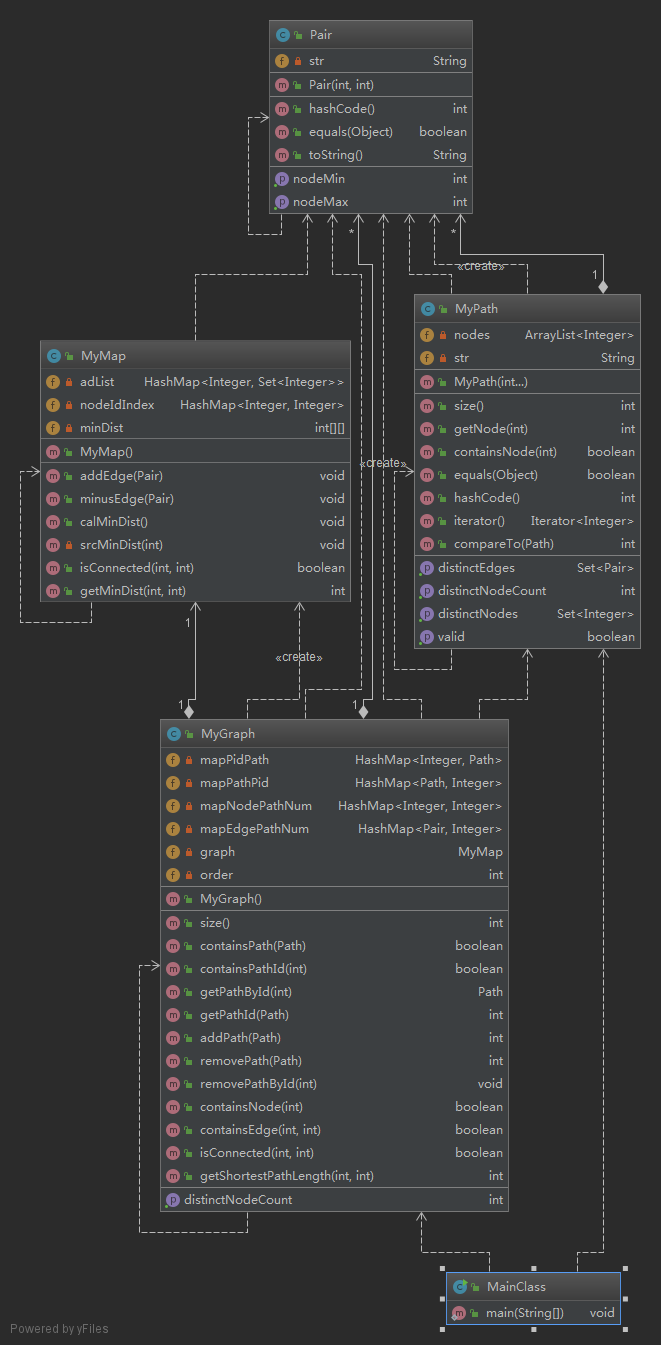
MyMap为所封装的图类,包含一个由HashMap实现的邻接表以及一个距离矩阵,如下所示,此外,为了用矩阵存储距离,需要一个结点Id到矩阵下标的映射。通过缓存距离矩阵,将距离计算得到的结果记录下来,加速对距离查询的操作。距离矩阵除了可以实现查询距离的功能之外,还可以判断结点之间的连通性。
private HashMap<Integer, Set<Integer>> adList; //邻接表,维护无重边、有环、可自环的无向图 private HashMap<Integer,Integer> nodeIdIndex; //结点ID到矩阵下标的映射 private int[][] minDist; //最短距离矩阵,-1:不连通,>=0:最短距离
由于本次作业中改变图结构的指令数目很少,因此,我决定在每次改变图结构之后采用Dijstra算法计算全部点到点的距离,这样之后对于结点间距离和连通性的查询均可通过直接访问矩阵得到,时间复杂度为O(1)。并且,由于每条边的距离权重都是1,因此,Dijstra在这次作业中不需要松弛操作,单源点Dijstra的时间复杂度本质上与广搜相同,时间复杂度为O(V+E)。虽然这种一开始算出来全部距离的方法可以降低查询的时间复杂度,但是却会产生一些额外的时间消耗,比如:某两个结点间的距离始终没有被查询过,一开始将其计算出来相当于白白浪费了时间。
此外,本次作业加入了对图中边的查询,为了充分利用第一次作业中的结构,我将MyPath和MyGraph在原来的基础上进行了扩展,其所维护的结构如下:
MyPath:
private ArrayList<Integer> nodes; private Set<Integer> distinctNodes; private Set<Pair> distinctEdges;
MyGraph:
private HashMap<Integer, Path> mapPidPath; private HashMap<Path,Integer> mapPathPid; private HashMap<Integer,Integer> mapNodePathNum; private HashMap<Pair,Integer> mapEdgePathNum; private MyMap graph;
其中,新增的mapEdgePathNum和distinctEdges与mapNodePathNum和distinctNodes的功能、意义类似。
可见,第二次作业在架构方面仅仅是在第一次作业上的扩充,MyPath中增加了对路径中不重复边集的维护,MyGraph中增加了对边到路径数目对应关系的维护,并没有做太大的重写,重写部分也仅仅涉及MyGraph中增删路径的操作,增加对新增结构的维护,对于原有结构的维护,与第一次作业相同。
3. 第三次作业
第三次作业的难度比前两次大了很多,需要选择合适的算法。我采用拆点的算法实现了对距离、最小换乘次数、最小不满意度、最小票价(以下我们简称为”四个最小“)的求解。拆点算法的重点在于将一个点拆成多个相连通的点,表示换乘,但是拆点之后也存在一个问题,即,如果A被拆成了3个点,B被拆成了2个点,则求得的“四个最小”应该是3*2=6对点中的最小值,这样会增加时间复杂度。因此,为了解决这个问题,将一个点拆成x+1个点,x为经过这个点的路径数目,1表示一个总点,这个总点负责将拆得的一堆点连接起来,使他们相连通,同时,当求两点之间的“四个最小”时,即求两个总点之间的“四个最小”,从而加速算法,降低了时间复杂度。拆点后,图中的边有两种:路径中原有的边(称为”原有边“)和因拆点增加的边(称为“附加边”),附加边仅存在于总点与其他点之间。下图为一个简单换乘的拆点示意图:
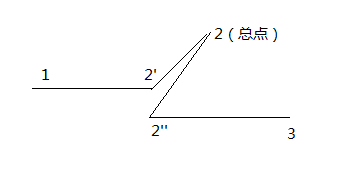
图中,2’和2‘’均为对2拆点得到的点,原有边为(1,2‘)和(2’‘,3),附加边为(2‘,2)和(2’‘,2)。
拆点之后,求”四个最小“依旧采用Dijstra算法,并设置边权如下:
- 最小距离:原有边为1,附加边为0。
- 最小换乘次数:原有边为0,附加边为0.5。
- 最小票价:原有边为1,附加边为1。
- 最小不满意度:原有边为U(E),附加边为16。
可见,附加边的权重为换乘代价的一半,则求得的“四个最小”为(两个总点之间的最小值-单次换乘代价)。
由于拆边使得路径结点的Id无法成为图中结点的唯一标识,因此采用(nodeId,pathId)作为唯一标识,相关的类与方法如下:
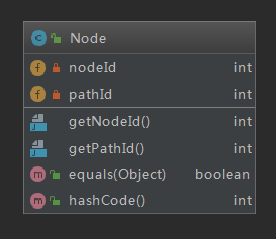
在第二次作业中,我将图的邻接表和距离矩阵封装到了一个类中,并将计算最短距离的算法也封装到了这个类中。经过分析后,第三次作业其实相当于对于四个相同结构、不同边权的图实施Dijstra算法,因此,将最短路径算法和图的邻接表封装到一个类里降低了操作的灵活度,于是我对第二次作业进行了重构,将图的邻接表和矩阵拆成两个不同的类MyMap和Buff,单独进行维护。得到的类图如下:
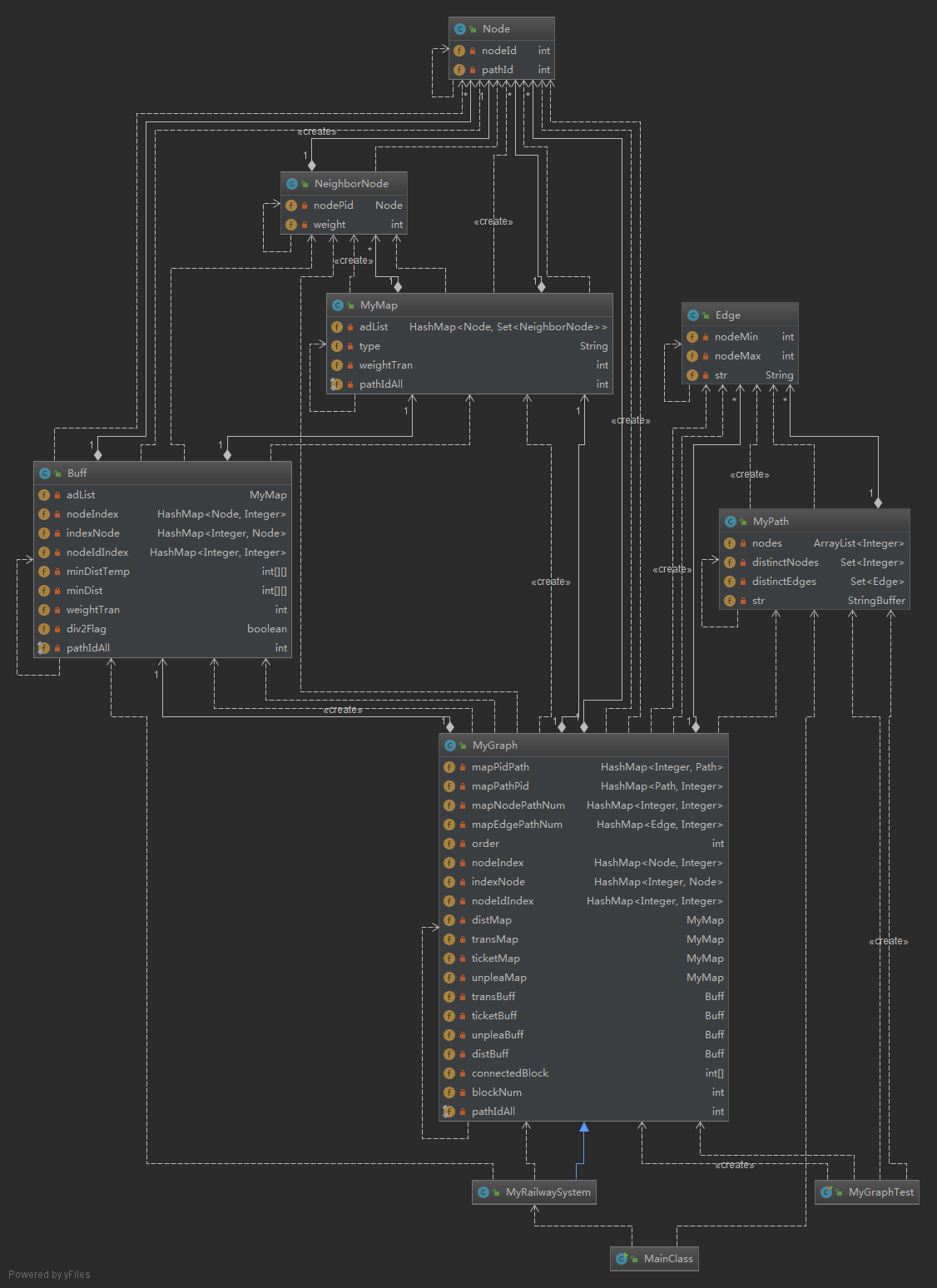
本次作业采用了继承,MyRailwaySystem继承了MyGraph,并对MyGraph进行重构,MyPath类中属性与第二次作业相同。
由于要求“四个最小”,因此需要在MyGraph中实例化四个图,分别记录距离、票价、换乘次数、不满意度,这四个图的结构是相同的,仅仅是边权不同,这意味着在改变图结构时,需要对这四个图统一做相似的改变。采用工厂模式构造,图(MyMap)中维护的结构如下,图类中仅包含改变图结构的相关方法(例如:加边,减边),不涉及最小值的计算。
MyMap:
private HashMap<Node, Set<NeighborNode>> adList; //邻接表 private String type; private int weightTran; //dist:0,transfer:1,ticket:1,unpleasant:16 private static final int pathIdAll = 0;//总点Id
其中,type属性用于表明图的类型(距离、票价、换乘次数或不满意度),weightTran则用于记录相应的换乘代价,由于在图中需要新增“总点”,而总点实际并不存在于任何一条路径中,其仅仅是用于算法优化的,又我们已知pathId一定大于零,因此设置总点的pathId为0,即(nodeId,0)表示结点对应的总点。
此外,在查询“四个最小”时,并没有延用第二次作业的“一改变图结构就全部重新算”的方法,而是采用指导书提出的滚雪球加速法,即,使用矩阵缓存“四个最小”的值,每次查询A到B两点的值时,如果这个值在缓存矩阵中不存在,则对A使用单源点Dijstra算法,并将A到所有点的结果存到矩阵中,方便下次直接查询;如果存在,则直接访问矩阵得到。为了能在查询时快速得到最小值,在Buff类中维护两个矩阵,如下:
private int[][] minDistTemp; //中间结果 private int[][] minDist; //最终结果
其中,中间结果矩阵中存了图中所有点之间的最小值,它的下标以(nodeId,pathId)为唯一标识,最大规模为4000+*4000+,而最终结果矩阵的下标仅以nodeId为标识,最大规模为120*120。因此,最终结果矩阵是用于查询的,而中间结果矩阵是用于计算的。由于缓存类Buff涉及计算最小值,因此,将计算最小值的Dijstra算法封装到这个类中,便于使用。
重写之后,MyGraph中维护的结构如下,增加了四个图和它对应的缓存矩阵用于计算“四个最小”,增加了connectedBlock数组和blockNum用于计算结点间连通性和连通块数目,其他结构与第二次作业相同:
private HashMap<Integer, Path> mapPidPath; private HashMap<Path,Integer> mapPathPid; private HashMap<Integer, Integer> mapNodePathNum; private HashMap<Edge,Integer> mapEdgePathNum; private MyMap distMap; private MyMap transMap; private MyMap ticketMap; private MyMap unpleaMap; private Buff transBuff; private Buff ticketBuff; private Buff unpleaBuff; private Buff distBuff; private int[] connectedBlock; //算连通性 private int blockNum;
连通性的计算也做了一定调整,在第二次作业中,通过查询距离矩阵得到结点的连通性,这是根据“不连通的结点间的最短距离无穷大”。第三次作业中,改用最大染色算法计算连通性,并得到连通块数目,其实质是广搜,当查询两个点的连通性时,在connectedBlock数组中找到对应的值,如果相同,则连通,否则,不连通。
将MyGraph重构之后,增删路径的方法也需要重写,在每次改变图结构时,需要重新算连通性,并初始化所有的缓存矩阵,用于记录新的图的最小值,对其他结构的维护与第二次作业相同。
四、bug及修复情况
在本系列作业中,对规格理解有偏差很容易出现bug,比如在第二次作业中,由于没有及时更新规格,我一度认为,结点自己到自己的边一定存在,导致中测出现问题,后来通过阅读更新后的规格发现:边存在,当且仅当,这条边存在于一条路径中。因此,正确理解规格很重要。
五、心得体会
经过这一单元规格的学习,我已经能够根据规格写出代码实现类的功能,但是在实验课上,由于对规格的运用不够熟练,以至于自己写规格的时候总会遇到这样那样拿不准的问题,而且自己在写的时候常常会出现规格描述不完善的情况,存在逻辑漏洞。
规格在团队合作中很重要,尤其是当对方要求你完成一定任务时,因为规格的描述基于数学知识,可以使用较少的JML规格代码描述一个较为复杂的方法,而且规格不同于自然语言,它的描述是确定的,不会产生歧义,避免了词不达意的问题。
此外,在三次作业中,由于OpenJML不能正确处理forall和exists关键词,运行时一直会产生一些奇怪的报错,我并没有使用JML的工具链测试,而是使用了Junit对代码的每个方法测试。Junit使用起来比较方便,并且能迅速定位错误位置,将bug的查找范围从一个工程缩小到某个具体的方法。在对JMLUnitNG的使用体验中,发现JMLUnitNG比较适用于对边界数据的检测,不太适用于对普通正常数据的检测。