【luogu P1471方差】题解

方差

题目背景

滚粗了的HansBug在收拾旧数学书，然而他发现了什么奇妙的东西。

题目描述

蒟蒻HansBug在一本数学书里面发现了一个神奇的数列，包含N个实数。他想算算这个数列的平均数和方差。

输入格式

第一行包含两个正整数N、M，分别表示数列中实数的个数和操作的个数。

第二行包含N个实数，其中第i个实数表示数列的第i项。

接下来M行，每行为一条操作，格式为以下两种之一：

操作1：1 x y k ，表示将第x到第y项每项加上k，k为一实数。

操作2：2 x y ，表示求出第x到第y项这一子数列的平均数。

操作3：3 x y ，表示求出第x到第y项这一子数列的方差。

输出格式

输出包含若干行，每行为一个实数，即依次为每一次操作2或操作3所得的结果（所有结果四舍五入保留4位小数）。

输入输出样例

输入 #1复制

5 5
1 5 4 2 3
2 1 4
3 1 5
1 1 1 1
1 2 2 -1
3 1 5

输出 #1复制

3.0000
2.0000
0.8000

说明/提示

样例说明：

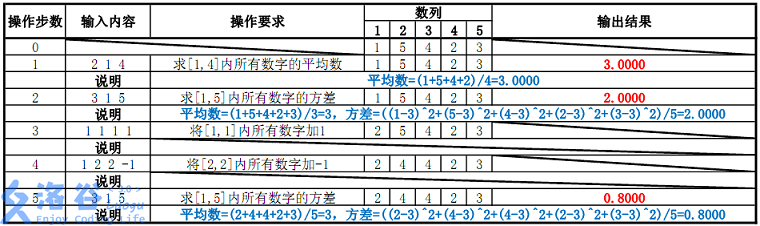
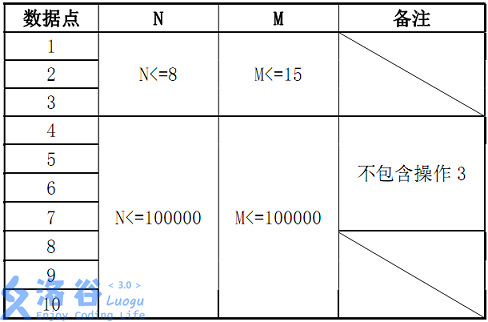
数据规模：

这题其实对方差公式和求平方和公式变形一下就可以简单很多。

以下偷来的推导过程。

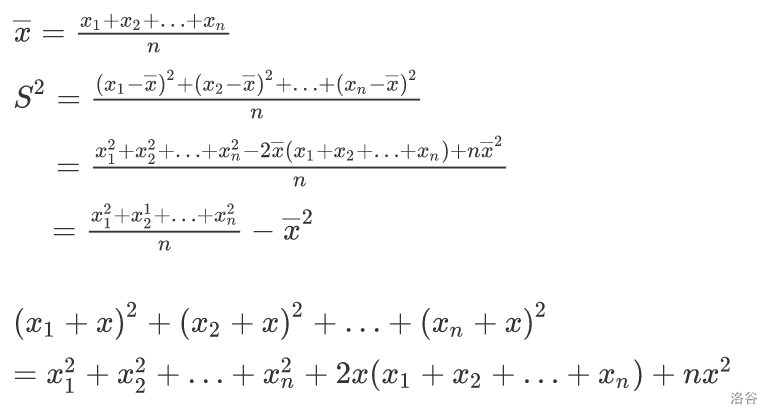
公式变形后，只需要用线段树进行区间修改和区间求和。

这里的区间求和求和需要记录sum1[]平方和，sum2[]普通和。

需要注意的有标记下传中是先更新sum1还是更新sum2？

sum1在更新时，需要加上未更新前的sum2，所以应当先更新sum1再更新sum2。

剩下几乎就是线段树模板了。

具体细节看代码，还有不要忘记开double。

#include<iostream>
#include<cstdio>
#define ls (k<<1)
#define rs (k<<1|1)
#define mid (x+y>>1)
using namespace std;
const int N=110000;
int n,m;
double s1,s2; 
double a[N<<2],sum1[N<<2],sum2[N<<2],lazy[N<<2];
inline void build(int k,int x,int y){//建树过程
    if(x==y){
        sum1[k]=a[x]*a[x];
        sum2[k]=a[x];
        return;
    }
    build(ls,x,mid);
    build(rs,mid+1,y);
    sum1[k]=sum1[ls]+sum1[rs];
    sum2[k]=sum2[ls]+sum2[rs];
}
inline void update(int k,int x,int y){
    sum1[ls]+=2.0*lazy[k]*sum2[ls]+(double)(mid-x+1)*lazy[k]*lazy[k];//需要先更新平方和。
    sum2[ls]+=(double)(mid-x+1)*lazy[k];
    sum1[rs]+=2.0*lazy[k]*sum2[rs]+(double)(y-(mid+1)+1)*lazy[k]*lazy[k];
    sum2[rs]+=(double)(y-(mid+1)+1)*lazy[k];
    lazy[ls]+=lazy[k];
    lazy[rs]+=lazy[k];
    lazy[k]=0;
}
inline void change(int k,int x,int y,int l,int r,double val){//val是double类型的。
    if(x>r||y<l) return;
    if(x>=l&&y<=r){
        lazy[k]+=val;
        sum1[k]+=2.0*val*sum2[k]+(double)(y-x+1)*val*val;
        sum2[k]+=(double)(y-x+1)*val;
        return;
    }
    if(lazy[k]) update(k,x,y);
    change(ls,x,mid,l,r,val);
    change(rs,mid+1,y,l,r,val);
    sum1[k]=sum1[ls]+sum1[rs];
    sum2[k]=sum2[ls]+sum2[rs];
}
inline void query(int k,int x,int y,int l,int r){
    if(x>r||y<l) return;
    if(x>=l&&y<=r){
        s1+=sum1[k];//s1记录查询区间的平方和
        s2+=sum2[k];//s2记录查询区间的和
        return;
    }
    if(lazy[k]) update(k,x,y);
    query(ls,x,mid,l,r);
    query(rs,mid+1,y,l,r);
}
int main()
{
    int i,j,op,x,y;
    double val,t;
    scanf("%d%d",&n,&m);
    for(i=1;i<=n;i++) 
    scanf("%lf",&a[i]);
    build(1,1,n);
    for(i=1;i<=m;i++){
        scanf("%d",&op);
        switch(op){
            case 1:{
                scanf("%d%d%lf",&x,&y,&val);
                change(1,1,n,x,y,val);
                break;
            }
            case 2:{
                scanf("%d%d",&x,&y);
                s1=s2=0;
                query(1,1,n,x,y);
                printf("%.4lf
",s2/(double)(y-x+1));
                break;
            }
            case 3:{
                scanf("%d%d",&x,&y);
                s1=s2=0;
                query(1,1,n,x,y);
                printf("%.4lf
",((s1/(double)(y-x+1)))-((s2/(double)(y-x+1)))*((s2)/(double)(y-x+1)));//方差公式的转化
                break;
            }
        }
    }
}