高斯分布的乘积

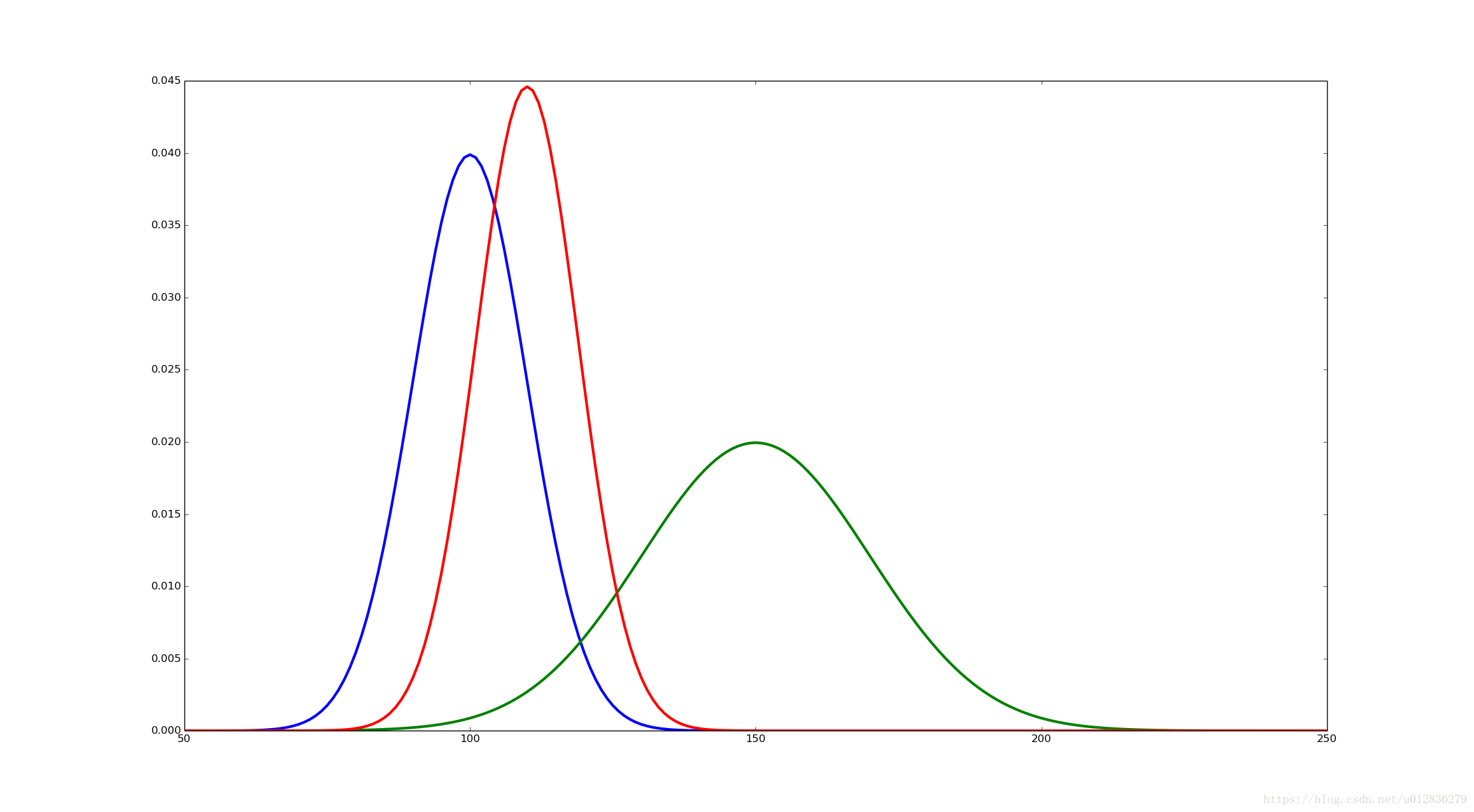
import matplotlib.pyplot as plt
from math import *

class Distribution:
    def __init__(self,mu,sigma,x,values,start,end):
        self.mu = mu
        self.sigma = sigma
        self.values = values
        self.x = x
        self.start = start
        self.end =end

    def normalize(self):
        s = float(sum(self.values))
        if s != 0.0:
            self.values = [i/s for i in self.values]

    def value(self, index):
        index -= self.start
        if index<0 or index >= len(self.values):
            return 0.0
        else:
            return self.values[index]

    @staticmethod
    def gaussian(mu,sigma,cut = 5.0):
        sigma2 = sigma*sigma
        extent = int(ceil(cut*sigma))
        values = []
        x_lim=[]
        for x in xrange(mu-extent,mu+extent+1):
            x_lim.append(x)
            values.append(exp((-0.5*(x-mu)*(x-mu))/sigma2))
        p1=Distribution(mu,sigma,x_lim,values,mu-extent,mu-extent+len(values))
        p1.normalize()
        return p1

if __name__=='__main__':
    p1 = Distribution.gaussian(100,10)
    plt.plot(p1.x,p1.values,"b-",linewidth=3)

    p2 = Distribution.gaussian(150,20)
    plt.plot(p2.x,p2.values,"g-",linewidth=3)

    start = min(p1.start,p2.start)
    end = max(p1.end,p2.end)
    mul_dist = []
    x_lim = []

    for index in range(start,end):
        x_lim.append(index)
        mul_dist.append(p1.value(index)*p2.value(index))
    #normalize the distribution
    s= float(sum(mul_dist))
    if s!=0.0:
        mul_dist=[i/s for i in mul_dist]

    plt.plot(x_lim,mul_dist,"r-",linewidth=3)
    plt.show()

参考链接：高斯分布的乘积