《数据结构》学习笔记 第7章 二叉搜索树 (BBST, AVL）

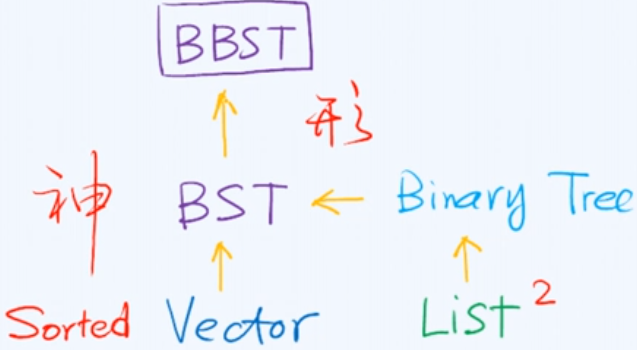
1， 二叉搜索树概述

• 

  • 对于Sorted Vector的借鉴尤为关键；

  • 平衡二叉搜索树（BBST）最能体现其强大功能！

• 定义： 结点含键值，且所有结点都满足“左孩子比父节点小，右孩子比父节点大”的二叉树。

• 性质：
  • 若任意节点的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
  • 任意节点的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
  • 任意节点的左、右子树也分别为二叉查找树；
  • 没有键值相等的节点。

2，BST的寻秩访问

• 各数据项之间，依照关键码的不同，彼此区分 （call-by-key）；
• 关键码需要支持的操作；比较与比对。
• 数据项，表现为词条的形式：
  • 

3，BST的顺序性与ADT

• 顺序性：只是对局部特征的刻画，却可以导出BST的整体特征；
• BST等价于中序遍历单调非降；
• ADT
  • 

  • 

4，BST的search操作

• 减而治之策略，实现：
•  
• 接口语义：成功时，指向该节点；失败时，指向试图转向的空节点。
• 算法复杂度：O(h).

5，BST的insert操作

• 算法（借助于search操作）：
  • 
  • 
• 复杂度：O(h).

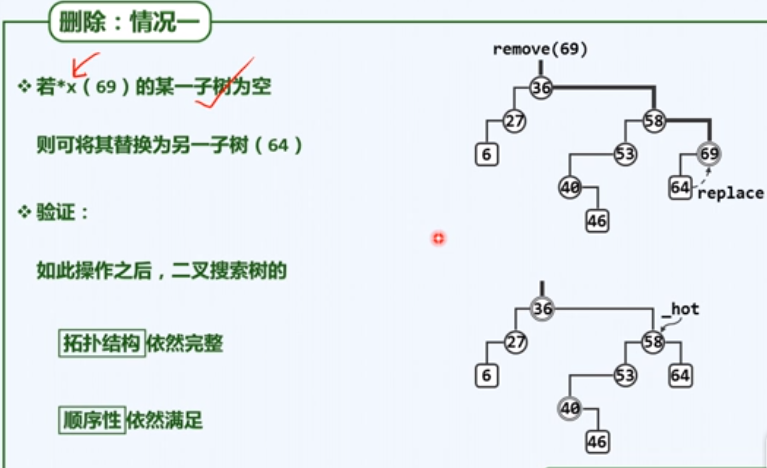
6，BST的remove操作

• 算法实现：
  • 
• 接下来，分：单分支和双分支两种情况处理。
  • 单分支算法及实现
    • 
    • 
  双分支算法：
  •  
  • 描述：如果待删除节点x有两棵子树，则要找到x在右子树中的后驱节点y，然后将y的右子树成为y的父结点的左子树，再用y替换掉x。
• 算法复杂度：O(h).

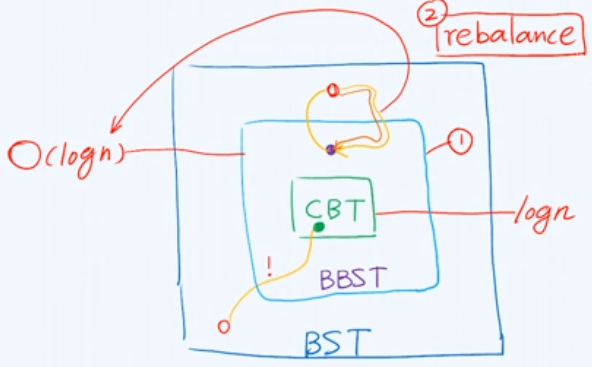
7，平衡二叉搜索树 （BBST）

• 包括AVL Tree，Red-Black Tree；目的：限制树高；
  • 随机生成与随机组成：平均意义上的树高，
  • 平衡的含义：树高为O(logN).
  • 理想BBST树高：log₍₂₎N.
  • 
• 中序遍历的歧义性
• 等价BST：上下可换，左右不乱；
• 等价BST的相互转换：等价变换+旋转调整 （Zig or Zag）

7.1 AVL Tree

• 概念综述：
  • 
• 各种BBST Tree的核心：
  • 1）如何界定一种适度的平衡标准；2）一整套重平衡的技巧与算法。
• AVL Tree的适度平衡标准：满足AVL平衡因子
  • 

  • 可以证明，AVL树的适度平衡- O(logN)。

• AVL ADT接口

• 主要操作：插入，删除 （相比于BST，增加重平衡步骤）

• 查找，重平衡 （connect34, rotateAt)等来自继承。 

• • 
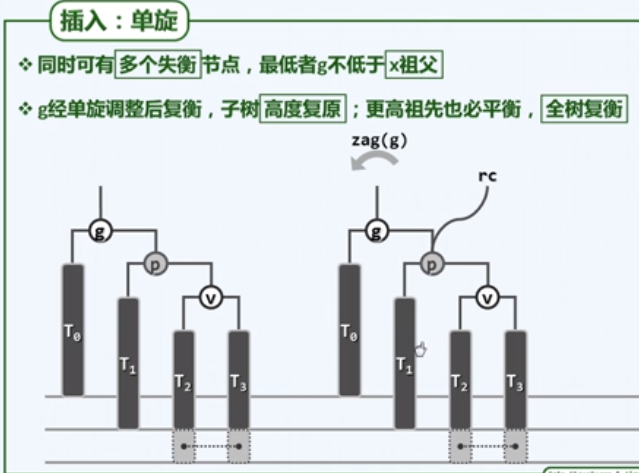
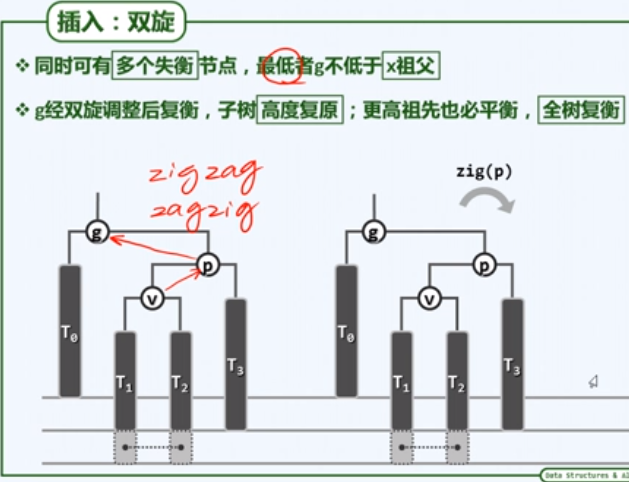
• AVL Tree插入操作 （插入后的复衡分为：单旋和双旋, 可使用3+4统一复衡算法）
  •     
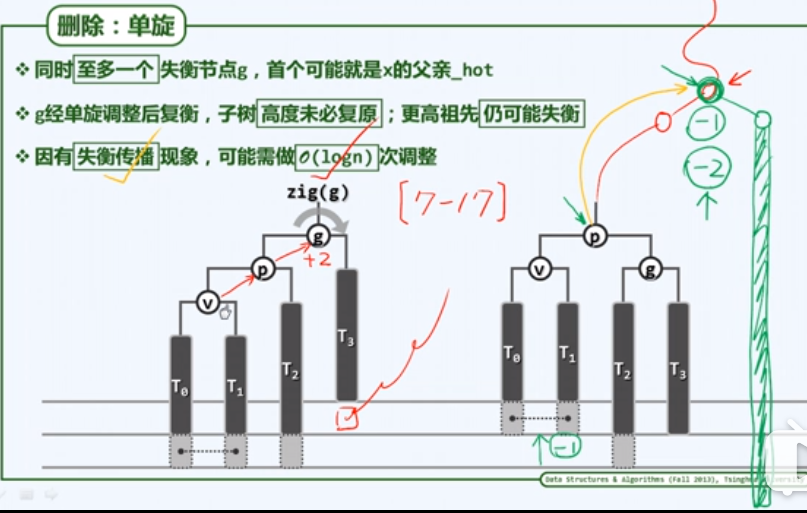
• AVL Tree删除操作 （删除后的复衡也分为：单旋和双旋, 可使用3+4统一复衡算法）
  • 

    • 被删除节点位于失衡节点g更短的分支，即T3底部。 

  • 

• AVL Tree综合评价

  •  

 更多参考资料：https://www.cnblogs.com/Joezzz/p/9610861.html