SPFA算法

SPFA算法

一.算法简介

SPFA(Shortest Path Faster Algorithm)算法是求单源最短路径的一种算法，它是Bellman-ford的队列优化，它是一种十分高效的最短路算法。

很多时候，给定的图存在负权边，这时类似Dijkstra等算法便没有了用武之地，而Bellman-Ford算法的复杂度又过高，SPFA算法便派上用场了。SPFA的复杂度大约是O(kE),k是每个点的平均进队次数(一般的，k是一个常数，在稀疏图中小于2)。

但是，SPFA算法稳定性较差，在稠密图中SPFA算法时间复杂度会退化。

实现方法：建立一个队列，初始时队列里只有起始点，在建立一个表格记录起始点到所有点的最短路径（该表格的初始值要赋为极大值，该点到他本身的路径赋为0）。然后执行松弛操作，用队列里有的点去刷新起始点到所有点的最短路，如果刷新成功且被刷新点不在队列中则把该点加入到队列最后。重复执行直到队列为空。

此外，SPFA算法还可以判断图中是否有负权环，即一个点入队次数超过N。

二.算法图解

给定一个有向图，求A~E的最短路。

源点A首先入队，并且AB松弛

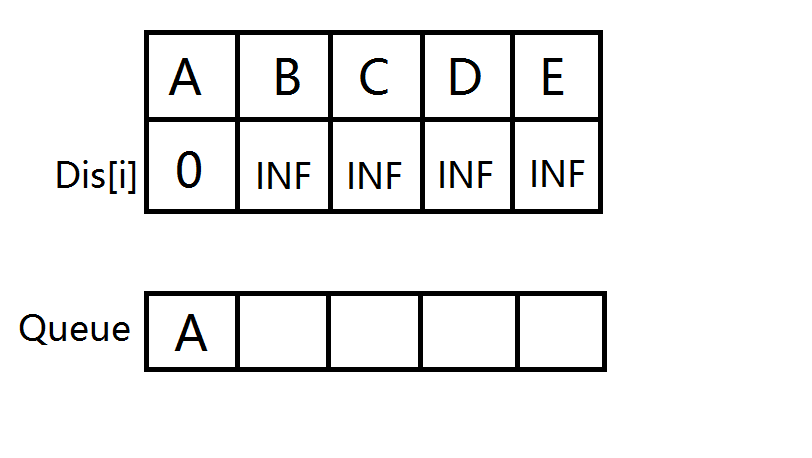
扩展与A相连的边，B，C 入队并松弛。

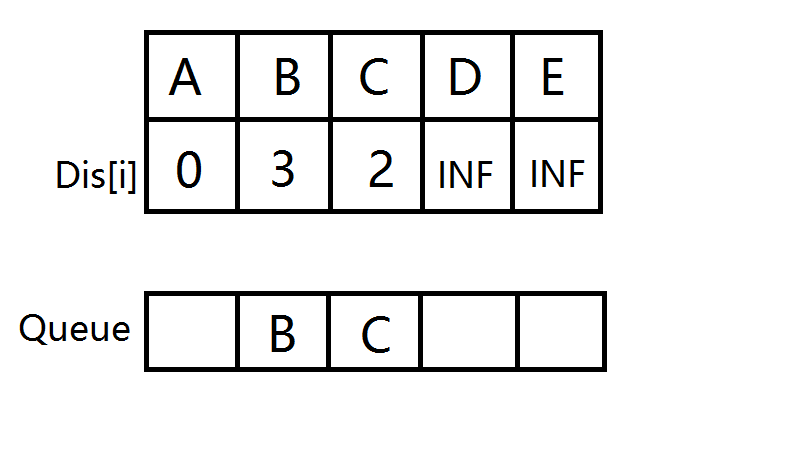
B，C分别开始扩展，D入队并松弛

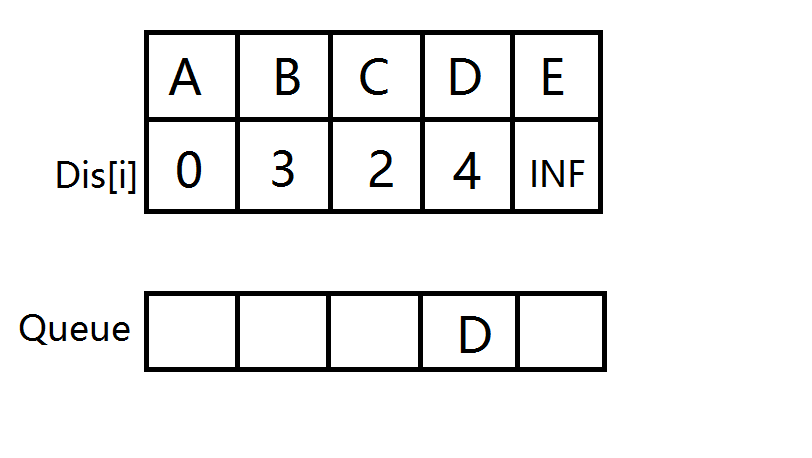
D出队，E入队并松弛。

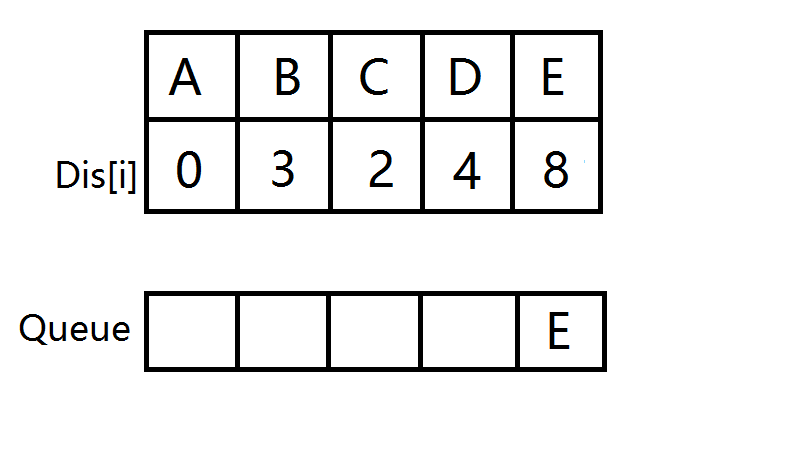
E出队，此时队列为空，源点到所有点的最短路已被找到，A->E的最短路即为8

以上就是SPFA算法的过程。

三.算法模板

#include "bits/stdc++.h"

using namespace std;
const int maxN = 200010 ;
struct Edge
{
    int    to , next , w ;
} e[ maxN ];

int    n,m,cnt,p[ maxN ],Dis[ maxN ];
int    In[maxN ];
bool    visited[ maxN ];

void    Add_Edge ( const int x , const int y , const int z )
{
    e[ ++cnt ] . to = y ;
    e[ cnt ] . next = p[ x ]; 
    e[ cnt ] . w = z ;
    p[ x ] = cnt ;
    return ;
}

bool    Spfa(const int S)
{
    int    i,t,temp;
    queue<int>    Q;
    memset ( visited , 0 , sizeof ( visited ) ) ; 
    memset ( Dis , 0x3f , sizeof ( Dis ) ) ; 
    memset ( In , 0 , sizeof ( In ) ) ;
    
    Q.push ( S ) ;
    visited [ S ] = true ;
    Dis [ S ] = 0 ;

    while( !Q.empty ( ) ) 
    {
        t = Q.front ( ) ;Q.pop ( ) ;visited [ t ] = false ;
        for( i=p[t] ; i ; i = e[ i ].next )
        {
            temp = e[ i ].to ;
            if( Dis[ temp ] > Dis[ t ] + e[ i ].w )
            {
                Dis[ temp ] =Dis[ t ] + e[ i ].w ;
                if( !visited[ temp ] )
                {
                    Q.push(temp);
                    visited[temp]=true;
                    if(++In[temp]>n)return false;
                }
            }
        }
    }
    return true;
}

int main ( )
{
    int    S , T ;

    scanf ( "%d%d%d%d" , &n , &m , &S , &T ) ;
    for(int i=1 ; i<=m ; ++i )
    {
        int x , y , _ ;
        scanf ( "%d%d%d" , &x , &y , &_ ) ;
        Add_Edge ( x , y , _  ) ;
    }

    if ( !Spfa ( S ) ) printf ( "FAIL!
" ) ;
    else               printf ( "%d
" , Dis[ T ] ) ;

    return 0;
}

(完)