什么是枪手博弈:
枪手博弈指彼此痛恨的甲乙丙三个枪手准备决斗。甲枪法最好,十发八中。乙枪法次之,十发六中。丙枪法最差,十发四中。假设他们了解彼此实力,也能做出理性判断。
问题一:如果三人同时开枪,并且每人每次只发一枪。若干轮枪战后,谁活下来的机会大?
问题二:如果三人轮流开枪,并且由枪法最差的丙先开枪,他该怎么做?
问题一:
分析:
3个人同时开枪,则枪手开枪的同时也可能被射死,4种情况,场上分别剩余(3,2,1,0)人
1)场上剩余3人,此时a(甲)一定向b(乙)射击,b一定向a射击,c(丙)可能向a射击或向空射击
2)场上剩余2人,互射,无其他可能
3)场上剩余1人,最后的胜利者
4)场上剩余0人,全部死亡
抽象出枪手模型
1 public class Hackbuteer { 2 private int state=1; //存活状态,1存活,0死亡 3 private double shot_rate; //命中率 4 public Hackbuteer(double shot_rate){ 5 this.shot_rate=shot_rate; 6 } 7 public int getState() { 8 return state; 9 } 10 public void setState(int state) { 11 this.state = state; 12 } 13 public double getShot_rate() { 14 return shot_rate; 15 } 16 public void setShot_rate(double shot_rate) { 17 this.shot_rate = shot_rate; 18 } 19 public boolean shot(Hackbuteer target) { 20 double rand = Math.random(); 21 if(rand<shot_rate){ //随机数小于命中率,表示命中 22 target.state=0; //目标死亡 23 return true; 24 } 25 return false; 26 } 27 }
模拟多次(100w)射击,用频率估算概率,代码如下:
1 public class HackbuteerTest { 2 public static void main(String[] args) { 3 int a_count=0; //a存活次数 4 int b_count=0; //b存活次数 5 int c_count=0; //c存活次数 6 for(int i=0;i<1000000;i++){ 7 Hackbuteer a=new Hackbuteer(0.8); 8 Hackbuteer b=new Hackbuteer(0.6); 9 Hackbuteer c=new Hackbuteer(0.4); 10 while(true){ 11 int all_state=a.getState()+b.getState()+c.getState(); //场上存活状态 12 if(all_state==3){ //3人都存活 13 a.shot(b); 14 b.shot(a); 15 //c.shot(a); //c向a射击;若模拟向空射击,则注释此行 16 }else if(all_state==2){ //1人死亡,2人存活 17 if(a.getState()==0){ 18 b.shot(c); 19 c.shot(b); 20 } 21 if(b.getState()==0){ 22 a.shot(c); 23 c.shot(a); 24 } 25 if(c.getState()==0){ 26 b.shot(a); 27 a.shot(b); 28 } 29 }else if(all_state==1 //仅有一人存活 30 || all_state==0 //无人存活 31 ){ 32 if(a.getState()==1){ 33 a_count++; 34 } 35 if(b.getState()==1){ 36 b_count++; 37 } 38 if(c.getState()==1){ 39 c_count++; 40 } 41 break; 42 } 43 44 } 45 } 46 System.out.println("a存活--"+a_count); 47 System.out.println("b存活--"+b_count); 48 System.out.println("c存活--"+c_count); 49 System.out.println("无人存活--"+(1000000-a_count-b_count-c_count)); 50 51 } 52 }
结果:
c向a射击 ,c向空射击
,c向空射击 ,
,
所以对于c来说,在同时开枪的情况下,c应该向a开枪,而不是向空开枪。
PS:以上结果仅代表实验100w次的频率,不完全代表概率。
问题二:
分析:
3人轮流开枪,c先开枪,依然是2种方案(向a射击,向空射击),代码如下:
1 public class HackbuteerTest2 { 2 public static void main(String[] args) { 3 int a_count=0; //a存活次数 4 int b_count=0; //b存活次数 5 int c_count=0; //c存活次数 6 for(int i=0;i<1000000;i++){ 7 Hackbuteer a=new Hackbuteer(0.8); 8 Hackbuteer b=new Hackbuteer(0.6); 9 Hackbuteer c=new Hackbuteer(0.4); 10 while(true){ 11 //c存活,开枪策略1,优先射击a 12 if(c.getState()==1){ 13 if(a.getState()==1){ 14 c.shot(a); 15 }else if(b.getState()==1){ 16 c.shot(b); 17 } 18 } 19 //c存活,开枪策略2,当a,b都存活时,不射击任何人 20 // if(c.getState()==1){ 21 // if(a.getState()==0 && b.getState()==1){ 22 // c.shot(b); 23 // }else if(a.getState()==1 && b.getState()==0){ 24 // c.shot(a); 25 // } 26 // } 27 28 //a存活,开枪策略,优先射击b 29 if(a.getState()==1){ 30 if(b.getState()==1){ 31 a.shot(b); 32 }else if(c.getState()==1){ 33 a.shot(c); 34 } 35 } 36 //b存活,开枪策略,优先射击a 37 if(b.getState()==1){ 38 if(a.getState()==1){ 39 b.shot(a); 40 }else if(c.getState()==1){ 41 b.shot(c); 42 } 43 } 44 45 if(a.getState()+b.getState()+c.getState()==1){ //仅有一人存活 46 if(a.getState()==1){ 47 a_count++; 48 } 49 if(b.getState()==1){ 50 b_count++; 51 } 52 if(c.getState()==1){ 53 c_count++; 54 } 55 break; 56 } 57 58 } 59 } 60 System.out.println("a存活--"+a_count); 61 System.out.println("b存活--"+b_count); 62 System.out.println("c存活--"+c_count); 63 } 64 }
结果:
c向a射击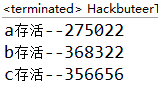 ,c向空射击
,c向空射击
显然,此时c应该向空射击,而不是向a射击
PS:当射击顺序为(c-b-a时,结论依然如此)
结论:
火并也要按照基本法,同时开枪有1/4-1/3的概率全部玩完(你是不是以为我要说什么实力很重要,选择很重要,背叛与忠诚?)