Spark算子---重分区

Spark性能调试是使用Spark的用户在进行大数据处理的时候必须面对的问题，性能调优的方法有很多，这里首先介绍一种常见的调优问题-小分区合并问题。

一：小分区合并问题介绍

在使用Spark进行数据处理的过程中，常常会使用filter方法来对数据进行一些预处理，过滤掉一些不符合条件的数据。

在使用该方法对数据进行频繁过滤或者是过滤掉的数据量过大的情况下就会造成大量小分区的生成。

在Spark内部会对每一个分区分配一个task执行，如果task过多，那么每个task处理的数据量很小，就会造成线程频繁的在task之间切换，使得资源开销较大，且很多任务等待执行，并行度不高，这会造成集群工作效益低下。

 为了解决这一个问题，常采用RDD中重分区的函数（coalesce函数或rePartition函数）来进行数据紧缩，减少分区数量，将小分区合并为大分区，从而提高效率

二：回顾宽、窄依赖

https://www.cnblogs.com/ssyfj/p/12556867.html

三：Coalesce()方法和rePartition()方法源码分析

（一）Coalesce()方法源码：

def coalesce(numPartitions: Int, shuffle: Boolean = false)(implicit ord: Ordering[T] = null)
    : RDD[T] = withScope {
  if (shuffle) {
    /** Distributes elements evenly across output partitions, starting from a random partition. */
    val distributePartition = (index: Int, items: Iterator[T]) => {
      var position = (new Random(index)).nextInt(numPartitions)
      items.map { t =>
        // Note that the hash code of the key will just be the key itself. The HashPartitioner
        // will mod it with the number of total partitions.
        position = position + 1
        (position, t)
      }
    } : Iterator[(Int, T)]

    // include a shuffle step so that our upstream tasks are still distributed
    new CoalescedRDD(
      new ShuffledRDD[Int, T, T](mapPartitionsWithIndex(distributePartition),
      new HashPartitioner(numPartitions)),
      numPartitions).values
  } else {
    new CoalescedRDD(this, numPartitions)
  }
}

（二）rePartition()方法源码：

  def repartition(numPartitions: Int)(implicit ord: Ordering[T] = null): RDD[T] = withScope {
    coalesce(numPartitions, shuffle = true)
  }

通过源码可以看出两者的区别：coalesce()方法的参数shuffle默认设置为false，repartition()方法就是coalesce()方法shuffle为true的情况。

四：使用场景

假设RDD有N个分区，需要重新划分成M个分区：

（一）N<M

N < M: 一般情况下N个分区有数据分布不均匀的状况，利用HashPartitioner函数将数据重新分区为M个，这时需要将shuffle设置为true。

因为重分区前后相当于宽依赖，会发生shuffle过程，此时可以使用coalesce(shuffle=true)，或者直接使用repartition()。

（二）N > M并且N和M相差不多(假如N是1000，M是100)

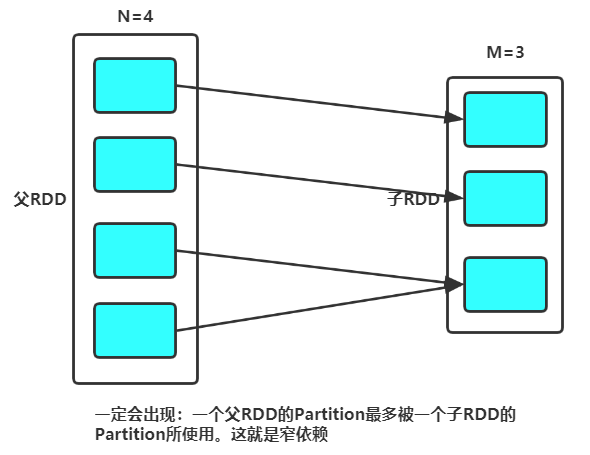
那么就可以将N个分区中的若干个分区合并成一个新的分区，最终合并为M个分区，这是前后是窄依赖关系，可以使用coalesce(shuffle=false)。

 （三）如果 N> M并且两者相差悬殊

这时如果将shuffle设置为false，父子ＲＤＤ是窄依赖关系，他们同处在一个Ｓｔａｇｅ中，就可能造成spark程序的并行度不够，从而影响性能，如果在M为1的时候，为了使coalesce之前的操作有更好的并行度，可以将shuffle设置为true。

（四）总结

如果传入的参数大于现有的分区数目，而shuffle为false，RDD的分区数不变，也就是说不经过shuffle，是无法将RDDde分区数变多的。---所以必须经过shuffle

五：补充repartitionAndSortWithinPartitions（RDD 重新分区，排序）

需求：将rdd数据中相同班级的学生分到一个partition中，并根据分数降序排序。

（一）repartitionAndSortWithinPartitions优势

此实例用到的repartitionAndSortWithinPartitions是Spark官网推荐的一个算子，官方建议，如果需要在repartition重分区之后，还要进行排序，建议直接使用repartitionAndSortWithinPartitions算子。

因为该算子可以一边进行重分区的shuffle操作，一边进行排序。shuffle与sort两个操作同时进行，比先shuffle再sort来说，性能可能是要高的。

六：算子代码演示

（一）coalesce（默认减少分区）

public static void coalesce(){
        List<Integer> list = Arrays.asList(1, 2, 3, 4, 5, 6, 7, 8, 9);
        JavaRDD<Integer> listRDD = sc.parallelize(list, 3);
        listRDD.coalesce(1).foreach(new VoidFunction<Integer>() {
            @Override
            public void call(Integer num) throws Exception {
                System.out.print(num);
            }
        });
    }

public static void coalesce() {
        List<Integer> list = Arrays.asList(1, 2, 3, 4, 5, 6, 7, 8, 9);
        JavaRDD<Integer> listRDD = sc.parallelize(list, 3);
        listRDD.coalesce(1).foreach(num -> System.out.println(num));
    }

def coalesce(): Unit = {
    val list = List(1,2,3,4,5,6,7,8,9)
    sc.parallelize(list,3).coalesce(1).foreach(println(_))
  }

（二）replication（增加分区）

 public static void replication(){
        List<Integer> list = Arrays.asList(1, 2, 3, 4);
        JavaRDD<Integer> listRDD = sc.parallelize(list, 1);
        listRDD.repartition(2).foreach(new VoidFunction<Integer>() {
            @Override
            public void call(Integer num) throws Exception {
                System.out.println(num);
            }
        });
    }

public static void replication(){
        List<Integer> list = Arrays.asList(1, 2, 3, 4);
        JavaRDD<Integer> listRDD = sc.parallelize(list, 1);
        listRDD.repartition(2).foreach(num -> System.out.println(num));
    }

def replication(): Unit ={
    val list = List(1,2,3,4)
    val listRDD = sc.parallelize(list,1)
    listRDD.repartition(2).foreach(println(_))
  }

（三）repartitionAndSortWithinPartitions

repartitionAndSortWithinPartitions函数是repartition函数的变种，与repartition函数不同的是，repartitionAndSortWithinPartitions在给定的partitioner内部进行排序，性能比repartition要高。

public static void repartitionAndSortWithinPartitions(){
        List<Integer> list = Arrays.asList(1, 3, 55, 77, 33, 5, 23);
        JavaRDD<Integer> listRDD = sc.parallelize(list, 1);
        JavaPairRDD<Integer, Integer> pairRDD = listRDD.mapToPair(new PairFunction<Integer, Integer, Integer>() {
            @Override
            public Tuple2<Integer, Integer> call(Integer num) throws Exception {
                return new Tuple2<>(num, num);
            }
        });
        JavaPairRDD<Integer, Integer> parationRDD = pairRDD.repartitionAndSortWithinPartitions(new Partitioner() {
            @Override
            public int getPartition(Object key) {
                Integer index = Integer.valueOf(key.toString());
                if (index % 2 == 0) {
                    return 0;
                } else {
                    return 1;
                }

            }

            @Override
            public int numPartitions() {
                return 2;
            }
        });
        parationRDD.mapPartitionsWithIndex(new Function2<Integer, Iterator<Tuple2<Integer, Integer>>, Iterator<String>>() {
            @Override
            public  Iterator<String> call(Integer index, Iterator<Tuple2<Integer, Integer>> iterator) throws Exception {
                final ArrayList<String> list1 = new ArrayList<>();
                while (iterator.hasNext()){
                    list1.add(index+"_"+iterator.next());
                }
                return list1.iterator();
            }
        },false).foreach(new VoidFunction<String>() {
            @Override
            public void call(String s) throws Exception {
                System.out.println(s);
            }
        });
    }

public static void repartitionAndSortWithinPartitions(){
        List<Integer> list = Arrays.asList(1, 4, 55, 66, 33, 48, 23);
        JavaRDD<Integer> listRDD = sc.parallelize(list, 1);
        JavaPairRDD<Integer, Integer> pairRDD = listRDD.mapToPair(num -> new Tuple2<>(num, num));
        pairRDD.repartitionAndSortWithinPartitions(new HashPartitioner(2))
                .mapPartitionsWithIndex((index,iterator) -> {
                    ArrayList<String> list1 = new ArrayList<>();
                    while (iterator.hasNext()){
                        list1.add(index+"_"+iterator.next());
                    }
                    return list1.iterator();
                },false)
                .foreach(str -> System.out.println(str));
    }

def repartitionAndSortWithinPartitions(): Unit ={
    val list = List(1, 4, 55, 66, 33, 48, 23)
    val listRDD = sc.parallelize(list,1)
    listRDD.map(num => (num,num))
      .repartitionAndSortWithinPartitions(new HashPartitioner(2))
      .mapPartitionsWithIndex((index,iterator) => {
        val listBuffer: ListBuffer[String] = new ListBuffer
        while (iterator.hasNext) {
          listBuffer.append(index + "_" + iterator.next())
        }
        listBuffer.iterator
      },false)
      .foreach(println(_))

  }

更多算子示例：https://www.cnblogs.com/qingyunzong/p/8922135.html